数学必修 第一册4.2 指数函数课文课件ppt

这是一份数学必修 第一册4.2 指数函数课文课件ppt，共20页。PPT课件主要包含了整体感知，新知探究，增函数，减函数，发现该城市人口经过，归纳小结，目标检测等内容，欢迎下载使用。
　　对于具体的函数，我们一般按照“背景—概念—图象和性质—应用”的路径进行研究．前面一节我们从具有现实背景的问题中，学习得到了指数函数的概念，接下来就要研究它的图象和性质，并灵活应用．根据我们在第三章研究幂函数的经验思考：如何研究一个函数的性质？研究一个函数的性质主要是研究哪些方面？
　　研究指数函数的图象和性质，首先要作出函数的图象，其次再根据图象概括函数的性质，最后还可以由性质进一步分析函数的图象．按照函数研究的一般过程，需要研究指数函数的定义域、值域、单调性、奇偶性，以及其特有的一些性质．
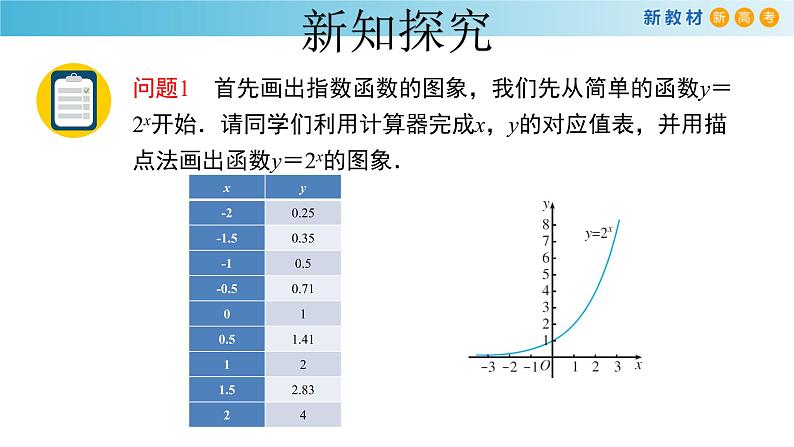
问题1　首先画出指数函数的图象，我们先从简单的函数y＝2x开始．请同学们利用计算器完成x，y的对应值表，并用描点法画出函数y＝2x的图象．
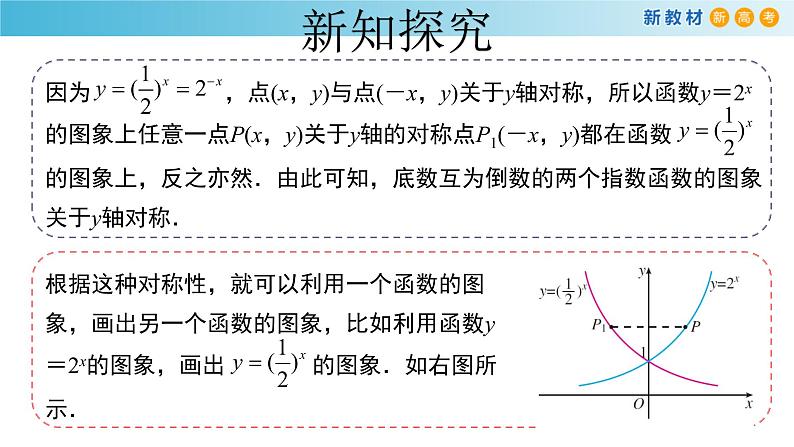
问题2　为了得到指数函数y＝ax(a＞0，且a≠1)的性质，我们还需要画出更多的具体指数函数的图象进行观察．用同样的方法，在同一直角坐标系内画出函数 的图象，并与函数y＝2x的图象进行比较，它们有什么关系？能否利用函数y＝2x的图象，画出函数 的图象？
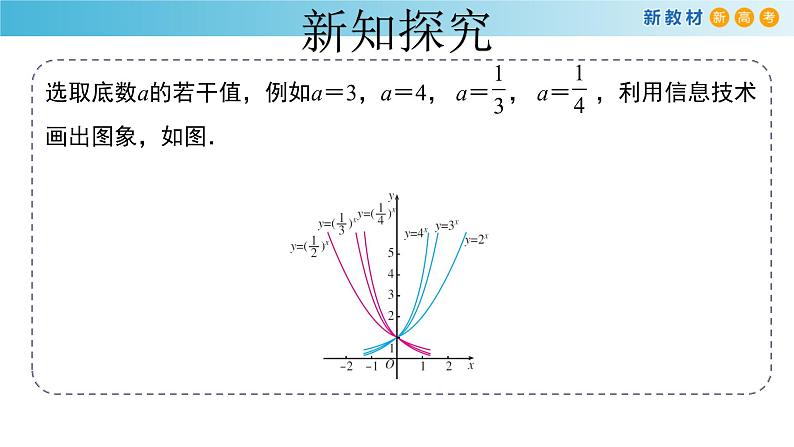
问题3　选取底数a(a＞0，且a≠1)的若干个不同的值，例如a＝3，a＝4， a＝ ， a＝ 在同一直角坐标系内画出相应的指数函数的图象，观察这些图象的位置、公共点和变化趋势，它们有哪些共性？根据你所概括出的结论，自己设计一个表格，写出指数函数y＝ax(a＞0，且a≠1)的定义域、值域、单调性、奇偶性，等等．
指数函数y＝ax(a>0，且a≠1)的图象和性质如下表：
例1　比较下列各题中两个值的大小：
（1）1.72.5，1.73； （2） ， ； （3）1.70.3，0.93.1．
解：（1）1.72.5和1.73可看作函数y＝1.7x ，
当x分别取2.5和3时所对应的两个函数值．
因为底数1.7＞1，所以指数函数y＝1.7x是增函数．
因为2.5＜3，所以1.72.5＜1.73．
解： （2）同（1）理，
因为0＜0.8＜1，所以指数函数y＝0.8x是减函数．
解：（3）由指数函数的特性知1.70.3＞1.70＝1，0.93.1＜0.90＝1，
所以1.70.3＞0.93.1．
例2　如右图，某城市人口呈指数增长．
（1）根据图象，估计该城市人口每翻一番所需的时间（倍增期）；
解： （1）观察图象，
20年约为10万，经过40年约为20万，
即由10万人口增加到20万人口所用的时间约为20年，
所以该城市人口每翻一番所需的时间约为20年．
（2）该城市人口从80万人开始，经过20年会增长到多少万人？
解： （2）因为倍增期为20年，所以每经过20年，
因此，从20万人开始，经过20年，
该城市人口大约会增长到160万人．
问题4　本节课研究指数函数的图象和性质的方法是什么？从哪几方面概括了指数函数的性质？分别是什么？
在同一直角坐标系中画出函数 和 的图象，并说明它们的关系．
比较下列各题中两个值的大小：
（1） ， ； （2）0.3－3.5，0.3－2.3； （3）1.20.5，0.51.2．
（2）0.3－3.5＞0.3－2.3．
（3）1.20.5＞0.51.2．
体内癌细胞初期增加得很缓慢，但到了晚期就急剧增加，画一幅能反映体内癌细胞数量随时间变化的示意图．
答案：可用指数函数S＝S0at来刻画体内癌细胞数量S随时间t变化的规律，其中初始量S0＞0，增长比例a＞1，t≥0．图略．