



初中数学人教版八年级上册12.3 角的平分线的性质教课ppt课件
展开角的平分线上的点到角的两边的距离相等.
几何表示:如图,∵OC是∠AOB的平分线,点P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.∴PD=PE.
1.探究并证明角的平分线的判定.2.会用角的平分线的判定解决实际问题.3.熟练掌握角的平分线的性质和角的平分线的判定的综合运用.
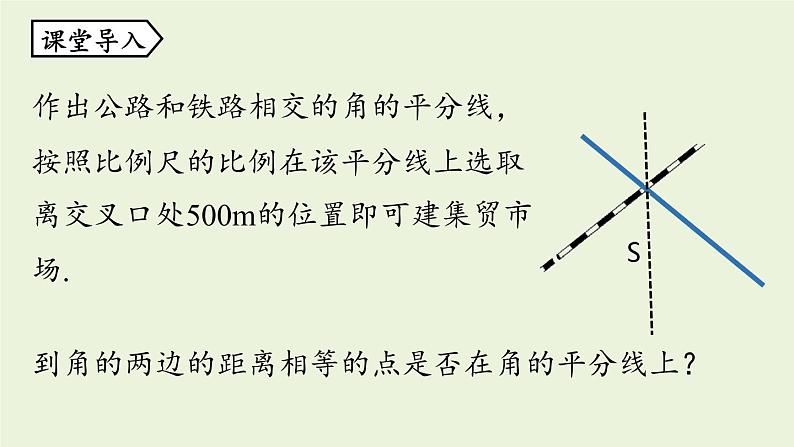
思考:如图,要在S区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路与铁路的交叉处500m.这个集贸市场应建于何处?
作出公路和铁路相交的角的平分线,按照比例尺的比例在该平分线上选取离交叉口处500m的位置即可建集贸市场.
到角的两边的距离相等的点是否在角的平分线上?
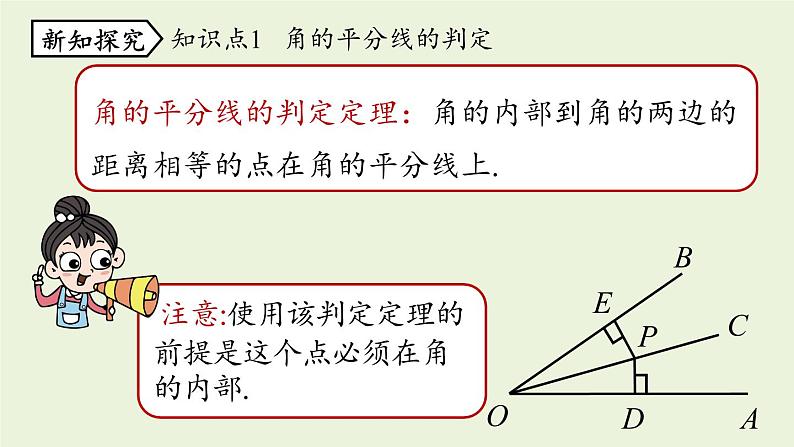
角的平分线的判定定理:角的内部到角的两边的距离相等的点在角的平分线上.
注意:使用该判定定理的前提是这个点必须在角的内部.
知识点1 角的平分线的判定
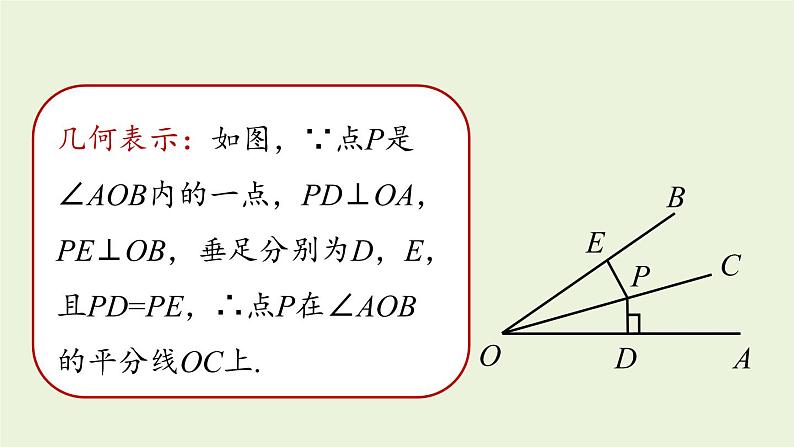
几何表示:如图,∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,∴点P在∠AOB的平分线OC上.
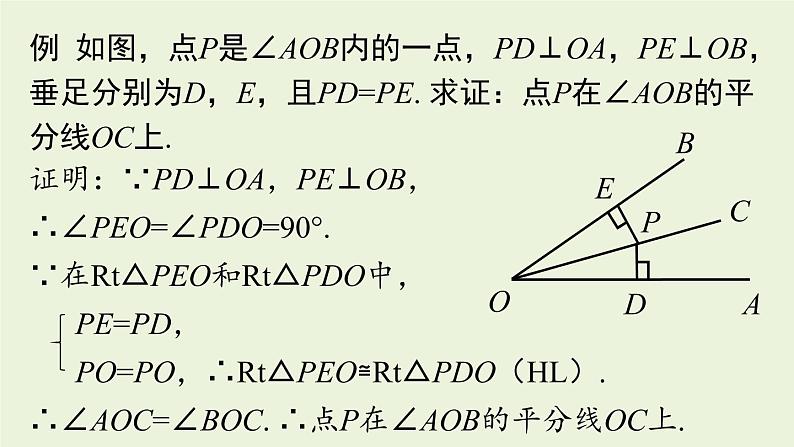
证明:∵PD⊥OA,PE⊥OB,∴∠PEO=∠PDO=90°.∵在Rt△PEO和Rt△PDO中, PE=PD, PO=PO,∴Rt△PEO≌Rt△PDO(HL). ∴∠AOC=∠BOC. ∴点P在∠AOB的平分线OC上.
例 如图,点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE. 求证:点P在∠AOB的平分线OC上.
角的平分线的性质定理与判定定理的关系.
点在角的平分线上
(角的内部)点到角的两边的距离相等
性质定理是证明两条线段相等的依据,判定定理是证明两个角相等的依据.
知识点2 角的平分线的性质定理与判定定理的关系
分别画出以下三角形的三个内角的角平分线,从位置的角度看你能得出什么结论?
三角形三个内角的角平分线的交点位于三角形的内部.
知识点3 三角形三个内角平分线的性质
过交点分别作三角形三边的垂线,测量一下每一组垂线段,从大小上你能观察出什么结论?
过交点作三角形三边的垂线段相等.
例 如图,△ABC的角平分线AD,BE,CF相交于点P.求证:点P到△ABC三边AB,BC,CA的距离相等.
证明:过点P作PM⊥BC,PN⊥AC,PO⊥AB,垂足分别为点M,N,O.
∵AD为△ABC的角平分线,∴PN=PO.∵BE为△ABC的角平分线, ∴PM=PO.∵CF为△ABC的角平分线,∴PM=PN.∴PM=PN=PO,即点P到△ABC三边AB,BC,CA的距离相等.
三角形三个内角的平分线的性质三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等.反之,三角形内部到三边距离相等的点是该三角形三条角平分线的交点.
判断题:(1)如图1,若QM=QN,则OQ平分∠AOB.( ) (2)如图2,若QM⊥OA于点M,QN⊥OB于点N,则OQ平分∠AOB.( )
1.如图,P是△ABC外部一点,PD⊥AB,交AB的延长线于点D,PE⊥AC,交AC的延长线于点E,PF⊥BC于点F,且PD=PE=PF.关于点P有下列三种说法:①点P在∠DBC的平分线上;②点P在∠BCE的平分线上;③点P在∠BAC的平分线上.其中说法正确的个数为( )A.0 B.1 C.2 D.3
2.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F且DB=DC. 求证:AD是∠BAC的平分线.
BE=CF,DB=DC.
Rt△BDE≌Rt△CDF.
DE⊥AB,DF⊥AC ,DE=DF.
AD是∠BAC的平分线.
(直角三角形全等(HL))
证明:∵DE⊥AB,DF⊥AC, ∴∠BED=∠CFD=90°. ∵在Rt△BDE和Rt△CDF中, BE=CF, DB=DC, ∴Rt△BDE≌Rt△CDF(HL). ∴DE=DF.∴点D在∠BAC的平分线上,即AD是∠BAC的平分线.
3.如图,O是△ABC内一点,O到三边AB,BC,CA的距离分别为OF,OD,OE,且OF=OD=OE,若∠BAC=70°,则∠BOC=( ).
证明:由题意,得OD⊥BC,OE ⊥ AC, OF ⊥ AB, 且OF=OD=OE,∴OB,OC分别平分∠ABC和∠ACB.∵∠BAC=70°,
∴∠ABC+∠ACB=180°-∠BAC=110°.
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
更多同类例题见《教材帮》数学RJ八上12.3节方法帮
4.如图,在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
证明:∵∠ADC+∠ABC=180°,∠ADC+∠EDC=180°,∴∠ABC=∠EDC.∵CE⊥AD,CF⊥AB, ∴∠CED=∠CFB=90°.∵在△BCF和△DCE中, ∠CFB=∠CED, ∠FBC=∠EDC, BC=DC, ∴△BCF≌△DCE(AAS). ∴CF=CE,即AC平分∠BAD.
学会用添加辅助线的方法解题
角的内部到角的两边的距离相等的点在角的平分线上
综合利用角的平分线的性质和判定来解决实际问题
1.如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE平分∠DAB.
证明:过点E作EF⊥AD于点F,∵∠B=∠C=90°, ∴DC⊥EC,EB⊥AB. ∵DE平分∠ADC, ∴EC=EF.
证明角平分线的方法只需从要证的线上的某一点向角的两边作(找)垂线段,再证明垂线段相等即可.
∵E是BC的中点, ∴EC=EB =EF.又∵EF⊥AD,EB⊥AB, ∴点E在∠DAB的平分线上,即AE平分∠DAB.
2.如图,∠MON=60°,点A,B为射线OM,ON上的动点(点A,B不与点O重合),在∠MON的内部,△AOB的外部有一点P,且AP=BP,∠APB=120°,求证:点P在∠MON的平分线上.
证明:①若∠PAO≠90°,如图,过点P分别作PC⊥OM,PD⊥ON,垂足分别为C,D,则∠ACP=∠BDP=90°.
在四边形OCPD中, ∠CPD=360°-∠OCP-∠COD-∠ODP=120°,∴∠APB=∠CPD. ∴∠APB-∠APD =∠CPD-∠APD,即∠APC=∠BPD. 在△APC和△BPD中, ∠APC=∠BPD, ∠ACP=∠BDP, AP=BP,∴△APC≌△BPD(AAS). ∴PC=PD, ∴点P在∠MON的平分线上.
数学12.3 角的平分线的性质课文ppt课件: 这是一份数学12.3 角的平分线的性质课文ppt课件,共14页。
初中人教版第十二章 全等三角形12.3 角的平分线的性质图文课件ppt: 这是一份初中人教版第十二章 全等三角形12.3 角的平分线的性质图文课件ppt,共28页。PPT课件主要包含了复习备用,几何语言,复习引入,学习目标,重点难点,新知探究,合作探究,归纳总结,学以致用,公共边等内容,欢迎下载使用。
2020-2021学年第十二章 全等三角形12.3 角的平分线的性质图片课件ppt: 这是一份2020-2021学年第十二章 全等三角形12.3 角的平分线的性质图片课件ppt,共1页。













