2020-2021学年安徽省芜湖市南陵县七年级（下）期末数学试卷

这是一份2020-2021学年安徽省芜湖市南陵县七年级（下）期末数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

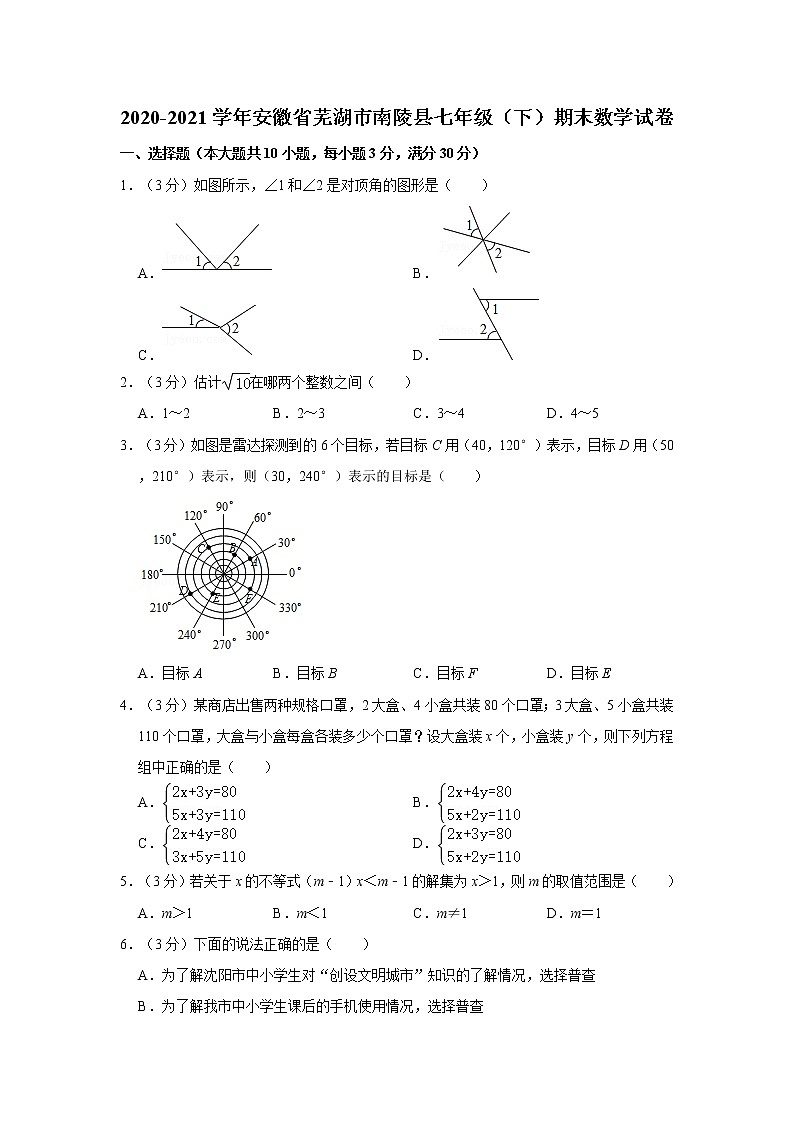
1．（3分）如图所示，∠1和∠2是对顶角的图形是（ ）
A．B．
C．D．
2．（3分）估计在哪两个整数之间（ ）
A．1～2B．2～3C．3～4D．4～5
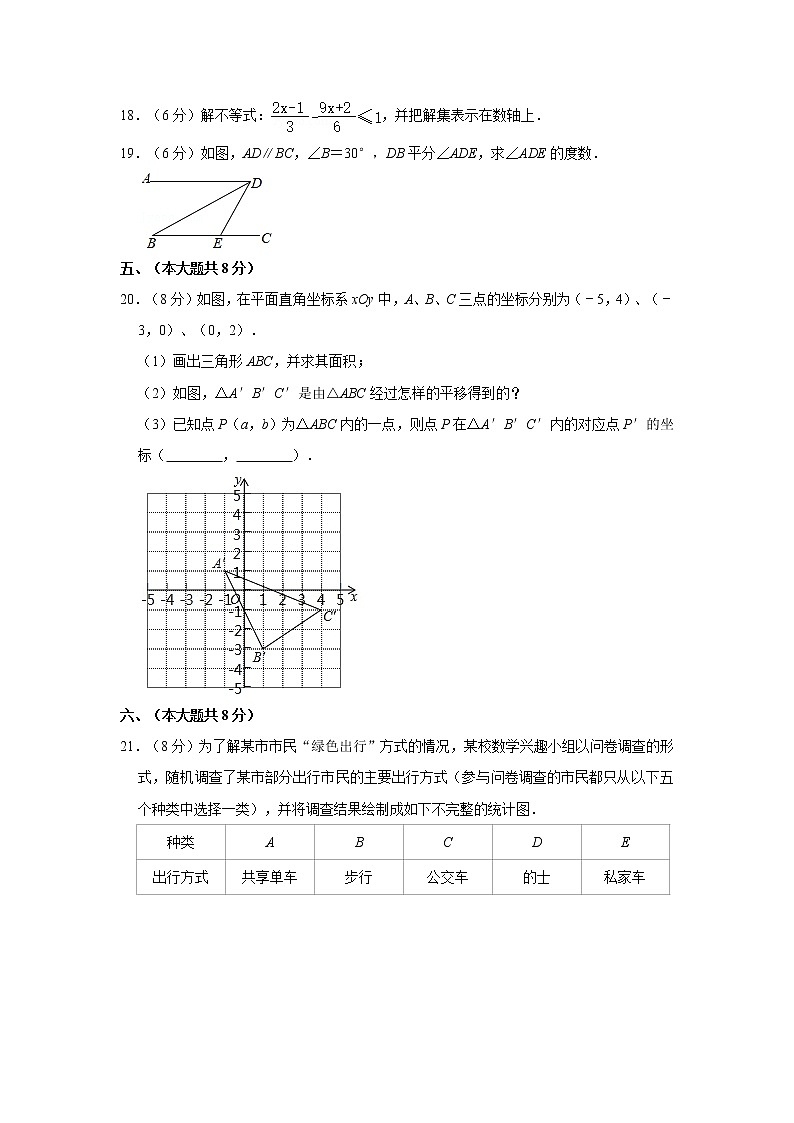
3．（3分）如图是雷达探测到的6个目标，若目标C用（40，120°）表示，目标D用（50，210°）表示，则（30，240°）表示的目标是（ ）
A．目标AB．目标BC．目标FD．目标E
4．（3分）某商店出售两种规格口罩，2大盒、4小盒共装80个口罩；3大盒、5小盒共装110个口罩，大盒与小盒每盒各装多少个口罩？设大盒装x个，小盒装y个，则下列方程组中正确的是（ ）
A．B．
C．D．
5．（3分）若关于x的不等式（m﹣1）x＜m﹣1的解集为x＞1，则m的取值范围是（ ）
A．m＞1B．m＜1C．m≠1D．m＝1
6．（3分）下面的说法正确的是（ ）
A．为了解沈阳市中小学生对“创设文明城市”知识的了解情况，选择普查
B．为了解我市中小学生课后的手机使用情况，选择普查
C．为了解深圳市民垃圾分类的响应情况，选择普查
D．为确保“嫦娥五号”探测器顺利发射，对其全部零件进行普查
7．（3分）如图，D，E，F分别在△ABC的三边上，能判定DE∥AC的条件是（ ）
A．∠1+∠2＝180°B．∠1＝∠3C．∠2＝∠4D．∠3＝∠C
8．（3分）﹣64的立方根是（ ）
A．﹣4B．4C．±8D．±2
9．（3分）已知关于x、y的方程组与有相同的解，则a和b的值为（ ）
A．B．C．D．
10．（3分）若关于x的不等式组的整数解只有2个，则m的取值范围是（ ）
A．m＞﹣3B．m＜﹣2C．﹣3≤m＜﹣2D．﹣3＜m≤﹣2
二、填空题（本大题共5小题，每小题3分，满分15分）
11．（3分）的平方根是 ．
12．（3分）已知a＞b，则﹣4a+5 ﹣4b+5．（填＞、＝或＜）
13．（3分）若a+2b＝8，3a+4b＝18，则2a+3b的值为 ．
14．（3分）已知点P（a，b）到x轴的距离是2，到y轴的距离是5，且|a﹣b|＝a﹣b，则P点坐标是 ．
15．（3分）已知：，且3a+2b﹣4c＝9，则a+b+c的值等于 ．
三、解答题（本大题共2小题，每小题5分，满分10分）
16．（5分）计算：﹣12+（﹣2）3×﹣×（﹣）
17．（5分）解方程组：．
四、解答题（本大题共2小题，每小题6分，满分12分）
18．（6分）解不等式：，并把解集表示在数轴上．
19．（6分）如图，AD∥BC，∠B＝30°，DB平分∠ADE，求∠ADE的度数．
五、（本大题共8分）
20．（8分）如图，在平面直角坐标系xOy中，A、B、C三点的坐标分别为（﹣5，4）、（﹣3，0）、（0，2）．
（1）画出三角形ABC，并求其面积；
（2）如图，△A′B′C′是由△ABC经过怎样的平移得到的？
（3）已知点P（a，b）为△ABC内的一点，则点P在△A′B′C′内的对应点P′的坐标（ ， ）．
六、（本大题共8分）
21．（8分）为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．
根据以上信息，回答下列问题：
（1）参与本次问卷调查的市民共有 人，其中选择B类的人数有 人；
（2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；
（3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．
七、（本大题8分）
22．（8分）如图，在△ABC中，点D、F在BC边上，点E在AB边上，点G在AC边上，EF与GD的延长线交于点H，∠CDG＝∠B，∠1+∠FEA＝180°．
求证：（1）EH∥AD；
（2）∠BAD＝∠H．
八、（本大题9分）
23．（9分）2021年5月19日全国徒步日，某社团组织爬山活动．组委会（活动主办方）为了奖励活动中取得了好成绩的参赛选手，计划购买共100件的甲、乙两种纪念品发放，其中甲种纪念品每件售价120元，乙种纪念品每件售价80元．
（1）如果购买甲、乙两种纪念品一共花费了9600元，求购买甲、乙两种纪念品各是多少件？
（2）设购买甲种纪念品m件，如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍，并且总费用不超过9400元．问组委会购买甲、乙两种纪念品共有几种方案？哪一种方案所需总费用最少？最少总费用是多少元？
2020-2021学年安徽省芜湖市南陵县七年级（下）期末数学试卷
参考答案与试题解析
一、选择题（本大题共10小题，每小题3分，满分30分）
1．（3分）如图所示，∠1和∠2是对顶角的图形是（ ）
A．B．
C．D．
【分析】根据对顶角的意义结合具体图形进行判断即可．
【解答】解：根据对顶角的意义，一个角的两条边分别是另一个角两边的反向延长线，这两个角是对顶角，
只有图B中的∠1和∠2是对顶角，
故选：B．
2．（3分）估计在哪两个整数之间（ ）
A．1～2B．2～3C．3～4D．4～5
【分析】由于32＝9，42＝16，由此可得的近似范围，然后分析选项可得答案．
【解答】解：由于32＝9，42＝16；
可得3＜＜4；
故选：C．
3．（3分）如图是雷达探测到的6个目标，若目标C用（40，120°）表示，目标D用（50，210°）表示，则（30，240°）表示的目标是（ ）
A．目标AB．目标BC．目标FD．目标E
【分析】根据位置的表示方法，第一个数表示距观察站的圈数×10，第二个数表示度数写出即可．
【解答】解：∵目标C用（40，120°）表示，目标D用（50，210°）表示，
∴第一个数表示距观察站的圈数，第二个数表示度数，
∴表示为（30，240°）的目标是：E．
故选：D．
4．（3分）某商店出售两种规格口罩，2大盒、4小盒共装80个口罩；3大盒、5小盒共装110个口罩，大盒与小盒每盒各装多少个口罩？设大盒装x个，小盒装y个，则下列方程组中正确的是（ ）
A．B．
C．D．
【分析】根据“2大盒、4小盒共装80个口罩；3大盒、5小盒共装110个口罩”，即可得出关于x，y的二元一次方程组，此题得解．
【解答】解：依题意得：．
故选：C．
5．（3分）若关于x的不等式（m﹣1）x＜m﹣1的解集为x＞1，则m的取值范围是（ ）
A．m＞1B．m＜1C．m≠1D．m＝1
【分析】根据不等式的基本性质3求解即可．
【解答】解：∵关于x的不等式（m﹣1）x＜m﹣1的解集为x＞1，
∴m﹣1＜0，
则m＜1，
故选：B．
6．（3分）下面的说法正确的是（ ）
A．为了解沈阳市中小学生对“创设文明城市”知识的了解情况，选择普查
B．为了解我市中小学生课后的手机使用情况，选择普查
C．为了解深圳市民垃圾分类的响应情况，选择普查
D．为确保“嫦娥五号”探测器顺利发射，对其全部零件进行普查
【分析】根据普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似解答．
【解答】解：A．为了解沈阳市中小学生对“创设文明城市”知识的了解情况，适合抽样调查，故A选项不合题意；
B．为了解我市中小学生课后的手机使用情况，适合抽样调查，故B选项不合题意；
C．为了解深圳市民垃圾分类的响应情况，适合抽样调查，故C选项不合题意；
D、为确保“嫦娥五号”探测器顺利发射，适合对其全部零件进行普查，故D选项符合题意．
故选：D．
7．（3分）如图，D，E，F分别在△ABC的三边上，能判定DE∥AC的条件是（ ）
A．∠1+∠2＝180°B．∠1＝∠3C．∠2＝∠4D．∠3＝∠C
【分析】直接利用平行线的判定方法分别分析得出答案．
【解答】解：A、当∠1+∠2＝180°时，EF∥BC，不符合题意；
B、当∠1＝∠3时，EF∥BC，不符合题意；
C、当∠2＝∠4时，无法得到DE∥AC，不符合题意；
D、当∠3＝∠C时，DE∥AC，符合题意．
故选：D．
8．（3分）﹣64的立方根是（ ）
A．﹣4B．4C．±8D．±2
【分析】直接根据立方根的定义可得答案．
【解答】解：∵（﹣4）3＝﹣64，
∴﹣64的立方根为：﹣4．
故选：A．
9．（3分）已知关于x、y的方程组与有相同的解，则a和b的值为（ ）
A．B．C．D．
【分析】利用方程组的解的定义，x、y满足4个方程，则先解2x+y＝5和x﹣y＝1组成的方程组，再把x、y代入另外两个方程得到关于a、b的方程组，然后解方程组求出a、b的值．
【解答】解：解方程组得，
把代入得，
解得．
故选：C．
10．（3分）若关于x的不等式组的整数解只有2个，则m的取值范围是（ ）
A．m＞﹣3B．m＜﹣2C．﹣3≤m＜﹣2D．﹣3＜m≤﹣2
【分析】首先解每个不等式，然后根据不等式组的整数的个数，确定整数解，从而确定m的范围．
【解答】解：，
解①得x≤﹣0.5，
解②得x＞m，
则不等式组的解集是m＜x≤﹣0.5．
由不等式组的整数解只有2个，得到整数解为﹣2，﹣1，
则m的范围为﹣3≤m＜﹣2，
故选：C．
二、填空题（本大题共5小题，每小题3分，满分15分）
11．（3分）的平方根是 ± ．
【分析】首先根据算术平方根的性质化简，再根据平方根的定义即可求出结果．
【解答】解：∵＝＝5，
∴的平方根是±．
故答案为：±．
12．（3分）已知a＞b，则﹣4a+5 ＜ ﹣4b+5．（填＞、＝或＜）
【分析】根据不等式的基本性质即可解决问题．
【解答】解：∵a＞b，
∴﹣4a＜﹣4b，
∴﹣4a+5＜﹣4b+5，
故答案为＜．
13．（3分）若a+2b＝8，3a+4b＝18，则2a+3b的值为 13 ．
【分析】已知两方程左右两边相加，计算即可求出所求．
【解答】解：联立得：，
①+②得：4a+6b＝26，即2（2a+3b）＝26，
则2a+3b＝13．
故答案为：13．
14．（3分）已知点P（a，b）到x轴的距离是2，到y轴的距离是5，且|a﹣b|＝a﹣b，则P点坐标是 （5，2）或（5，﹣2） ．
【分析】根据|a﹣b|＝a﹣b，分两种情况：a﹣b＝a﹣b或a﹣b＝﹣a+b，再根据点P（a，b）到x轴的距离是2，到y轴的距离是5，即可解答．
【解答】解：∵丨a﹣b丨＝a﹣b，
∴a﹣b＝a﹣b或a﹣b＝﹣a+b，
∵P（a，b）到x轴的距离是2，到y轴的距离是5，
∴a≠b，
∴a﹣b≠﹣a+b，
∴a＝5，b＝±2，
∴P点的坐标为（5，2）或（5，﹣2），
故答案为：（5，2）或（5，﹣2）．
15．（3分）已知：，且3a+2b﹣4c＝9，则a+b+c的值等于 ﹣15 ．
【分析】先设比例系数为k，代入3a+2b﹣4c＝9，转化为关于k的一元一次方程解答．
【解答】解：设＝＝＝k，
则a＝3k，b＝5k，c＝7k，
代入3a+2b﹣4c＝9，
得9k+10k﹣28k＝9，
解得：k＝﹣1，
∴a＝﹣3，b＝﹣5，c＝﹣7，
于是a+b+c＝﹣3﹣5﹣7＝﹣15．
故本题答案为：﹣15．
三、解答题（本大题共2小题，每小题5分，满分10分）
16．（5分）计算：﹣12+（﹣2）3×﹣×（﹣）
【分析】直接利用立方根的性质以及算术平方根的性质分别化简各数进而得出答案．
【解答】解：原式＝﹣1﹣8×+3×（﹣）
＝﹣1﹣1﹣1
＝﹣3．
17．（5分）解方程组：．
【分析】利用加减消元法对方程组进行求解即可．
【解答】解：，
①×3得：9x+12y＝30③，
②×4得：16x﹣12y＝20④，
③+④得：25x＝50，
解得：x＝2，
把x＝2代入①得：6+4y＝10，
解得：y＝1，
故原方程组的解为．
四、解答题（本大题共2小题，每小题6分，满分12分）
18．（6分）解不等式：，并把解集表示在数轴上．
【分析】首先两边同时乘以6去分母，再利用乘法分配律去括号，移项、合并同类项，最后把x的系数化为1即可．
【解答】解：去分母得：2（2x﹣1）﹣（9x+2）≤6，
去括号得：4x﹣2﹣9x﹣2≤6，
移项得：4x﹣9x≤6+2+2，
合并同类项得：﹣5x≤10，
把x的系数化为1得：x≥﹣2．
19．（6分）如图，AD∥BC，∠B＝30°，DB平分∠ADE，求∠ADE的度数．
【分析】直接利用平行线的性质以及角平分线的性质得出∠B＝∠ADB＝∠BDE，进而得出答案．
【解答】解：∵AD∥BC，
∴∠ADB＝∠B，
∵DB平分∠ADE，
∴∠ADB＝∠BDE，
∵∠B＝30°，
∴∠ADB＝∠BDE＝30°，
∴∠ADE＝∠ADB+∠BDE＝60°．
五、（本大题共8分）
20．（8分）如图，在平面直角坐标系xOy中，A、B、C三点的坐标分别为（﹣5，4）、（﹣3，0）、（0，2）．
（1）画出三角形ABC，并求其面积；
（2）如图，△A′B′C′是由△ABC经过怎样的平移得到的？
（3）已知点P（a，b）为△ABC内的一点，则点P在△A′B′C′内的对应点P′的坐标（ a+4 ， b﹣3 ）．
【分析】（1）根据A，B，C的坐标作出图形即可．
（2）根据平移变换的规律解决问题即可．
（3）利用平移规律解决问题即可．
【解答】解：（1）如图，△ABC即为所求．
S△ABC＝4×5﹣×2×4﹣×2×5﹣×2×3＝8；
（2）先向右平移4个单位，再向下平移3个单位．
（3）由题意P′（a+4，b﹣3）．
故答案为：a+4，b﹣3．
六、（本大题共8分）
21．（8分）为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．
根据以上信息，回答下列问题：
（1）参与本次问卷调查的市民共有 800 人，其中选择B类的人数有 240 人；
（2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；
（3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．
【分析】（1）由C类别人数及其百分比可得总人数，总人数乘以B类别百分比即可得；
（2）根据百分比之和为1求得A类别百分比，再乘以360°和总人数可分别求得；
（3）总人数乘以样本中A、B、C三类别百分比之和可得答案．
【解答】解：（1）本次调查的市民有200÷25%＝800（人），
∴B类别的人数为800×30%＝240（人），
故答案为：800，240；
（2）∵A类人数所占百分比为1﹣（30%+25%+14%+6%）＝25%，
∴A类对应扇形圆心角α的度数为360°×25%＝90°，A类的人数为800×25%＝200（人），
补全条形图如下：
（3）12×（25%+30%+25%）＝9.6（万人），
答：估计该市“绿色出行”方式的人数约为9.6万人．
七、（本大题8分）
22．（8分）如图，在△ABC中，点D、F在BC边上，点E在AB边上，点G在AC边上，EF与GD的延长线交于点H，∠CDG＝∠B，∠1+∠FEA＝180°．
求证：（1）EH∥AD；
（2）∠BAD＝∠H．
【分析】（1）先证DG∥AB，得出∠1＝∠BAD，则∠BAD+∠FEA＝180°，再根据平行线的判定即可得出结论；
（2）根据平行线的性质得出∠1＝∠H，即可得出结论．
【解答】证明：（1）∵∠CDG＝∠B，
∴DG∥AB，
∴∠1＝∠BAD，
∵∠1+∠FEA＝180°，
∴∠BAD+∠FEA＝180°，
∴EH∥AD；
（2）由（1）得：∠1＝∠BAD，EH∥AD，
∴∠1＝∠H，
∴∠BAD＝∠H．
八、（本大题9分）
23．（9分）2021年5月19日全国徒步日，某社团组织爬山活动．组委会（活动主办方）为了奖励活动中取得了好成绩的参赛选手，计划购买共100件的甲、乙两种纪念品发放，其中甲种纪念品每件售价120元，乙种纪念品每件售价80元．
（1）如果购买甲、乙两种纪念品一共花费了9600元，求购买甲、乙两种纪念品各是多少件？
（2）设购买甲种纪念品m件，如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍，并且总费用不超过9400元．问组委会购买甲、乙两种纪念品共有几种方案？哪一种方案所需总费用最少？最少总费用是多少元？
【分析】（1）设购买甲种纪念品x件，购买乙种纪念品y件，根据题意可得出二元一次方程组，解之即可得出结论；
（2）设购买甲种纪念品m件，则购买乙种纪念品（100﹣m）件，根据“购买乙种纪念品的件数不超过甲种纪念品的数量的2倍，并且总费用不超过9400元”，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，再结合m为整数即可得出各购买方案；利用总价＝单价×数量，可分别求出选择2个方案所需总费用，比较后即可得出结论．
【解答】解：（1）设购买甲种纪念品x件，购买乙种纪念品y件，
依题意得：，
解得：，
答：购买甲种纪念品40件，乙种纪念品60件．
（2）设购买甲种纪念品m件，则购买乙种纪念品（100﹣m）件，
依题意得：，
解得：33≤m≤35，
又∵m为整数，
∴m＝34或35，
∴共有2种购买方案，
方案1：购买甲种纪念品34件，乙种纪念品66件；
方案2：购买甲种纪念品35件，乙种纪念品65件．
选择方案1所需总费用为120×34+80×66＝9360（元），
选择方案2所需总费用为120×35+80×65＝9400（元）．
∵9360＜9400，
∴选择方案1所需总费用最少，最少费用为9360元．
种类
A
B
C
D
E
出行方式
共享单车
步行
公交车
的士
私家车
种类
A
B
C
D
E
出行方式
共享单车
步行
公交车
的士
私家车