2021高三数学第一轮复习 导学案 第12讲幂函数与二次函数

这是一份2021高三数学第一轮复习 导学案 第12讲幂函数与二次函数，共4页。学案主要包含了课前小测等内容，欢迎下载使用。
了解幂函数的概念；结合函数的图像，了解它们的变化情况。
理解二次函数的图像与性质，能用二次函数、方程、不等式之间的关系解决简单问题。
课前导引
要点预览
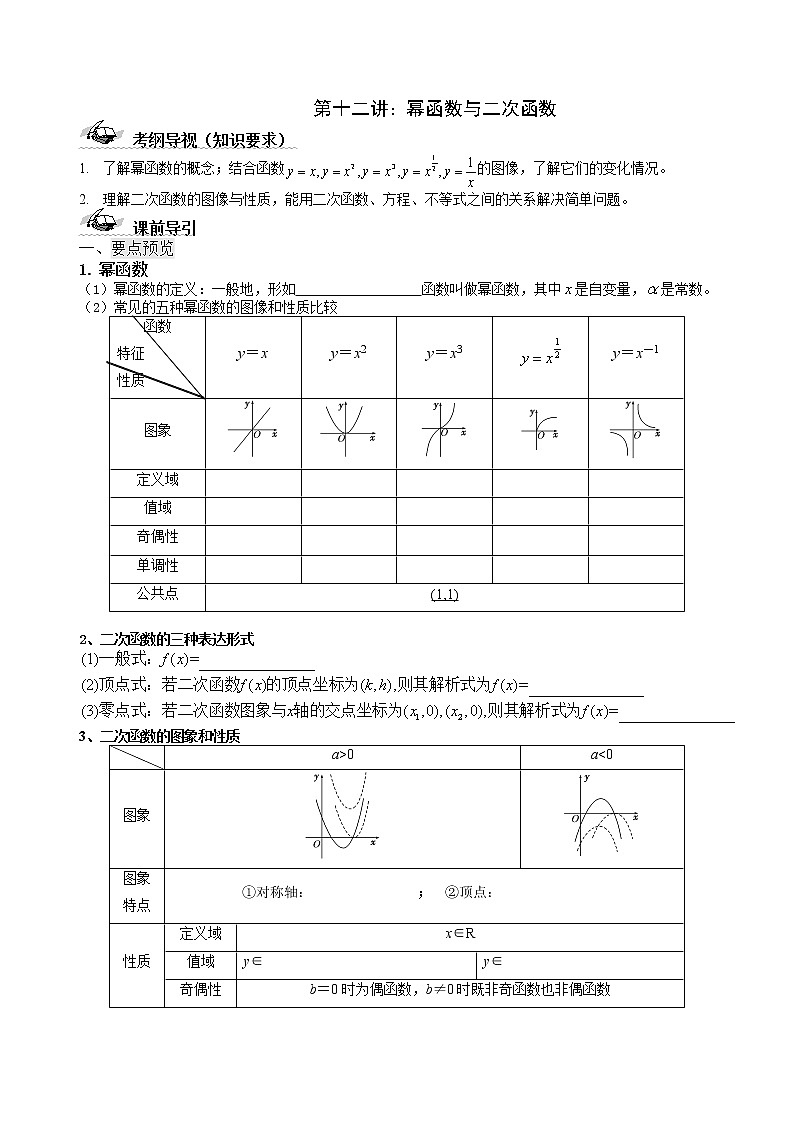
幂函数
（1）幂函数的定义：一般地，形如 函数叫做幂函数，其中是自变量，是常数。
常见的五种幂函数的图像和性质比较
2、二次函数的三种表达形式
3、二次函数的图象和性质
二、课前小测
1．下列函数中是幂函数的是( )．
A．y＝2x2 B．y＝eq \f(1,x2) C．y＝x2＋x D．y＝－eq \f(1,x)
2．已知函数f(x)＝4x2－mx＋5在区间[－2，＋∞)上是增函数，则f(1)的范围是( )．
A．f(1)≥25 B．f(1)＝25 C．f(1)≤25 D．f(1)＞25
3．若关于x的方程x2＋mx＋1＝0，有两个不相等的实数根，则实数m的取值范围是( )．
A．(－1,1) B．(－∞，－1)∪(1，＋∞) C．(－2,2) D．(－∞，－2)∪(2，＋∞)
4．函数的图象是( )．

5．二次函数y＝f(x)满足f(3＋x)＝f(3－x)(x∈R)且f(x)＝0有两个实根x1，x2，则x1＋x2＝________.
课堂导学
题型1：求二次函数的解析式
点评：求二次函数的解析式常利用待定系数法，但由于条件不同，则所选用的解析式不同，其方法也不同。
【变式迁移】
题型2：幂函数的图像及性质
（1）幂函数的图像经过点，则是（ ）
偶函数，且在上是增函数
偶函数，且在上是减函数
奇函数，且在上是减函数
非奇非偶函数，且在上是增函数
点评：在比较幂值时，必须结合幂值的特点，选择适当的函数，借助其单调性进行比较。
题型3：二次函数的图像与性质
点评：识别二次函数图像应学会“三看” （1.二次项系数2.对称轴3.特殊点）
【课堂小结】本节课你收获了什么
【课后作业】
若幂函数的图象过点，则( )
A、16 B、2 C、 D、
2.如图中曲线是幂函数y＝xn在第一象限的图象．已知n取±2，±eq \f(1,2)四个值，则相应于曲线C1，C2，C3，C4的n值依次为( )．
－2，－eq \f(1,2)，eq \f(1,2)，2 B．2，eq \f(1,2)，－eq \f(1,2)，－2
C．－eq \f(1,2)，－2,2，eq \f(1,2) D．2，eq \f(1,2)，－2，－eq \f(1,2)
3.已知f(x)＝1－(x－a)(x－b)(a＜b)，m，n是f(x)的零点，且m＜n，则a，b，m，n从小到大的顺序是________．
4．已知函数f(x)＝x2－2x＋2的定义域和值域均为[1，b]，则b等于( )．
A．3 B．2或3 C．2 D．1或2
5．若函数f(x)＝(x＋a)(bx＋2a)(常数a、b∈R)是偶函数，且它的值域为(－∞，4]，则该函数的解析式f(x)＝________.
函数
特征
性质
y＝x
y＝x2
y＝x3
y＝x－1
图象
定义域
值域
奇偶性
单调性
公共点
(1,1)
a>0
a