初中数学北京课改版八年级上册12.11 勾股定理示范课ppt课件

这是一份初中数学北京课改版八年级上册12.11 勾股定理示范课ppt课件，共23页。PPT课件主要包含了测量法，新知讲解，数格子法，勾股定理，争先恐后，个性化作业等内容，欢迎下载使用。

在古老的数学王国，有一种树木它很奇妙，生长速度大的惊人，它是什么呢？下面让我们带着这个疑问一同到数学王国去欣赏吧！
认识勾股定理，利用勾股定理进行简单的计算和实际运用;
体会数形结合思想和化归思想的运用，增强解决问题的能力;
进一步丰富数学活动经验，锻炼推理能力，感受勾股定理的文化价值.
自主学习任务1：阅读课本2页-3页，掌握下列知识要点。
勾股定理的内容是什么？本节课我们用什么方法发现了勾股定理？上述方法体现了什么数学思想？
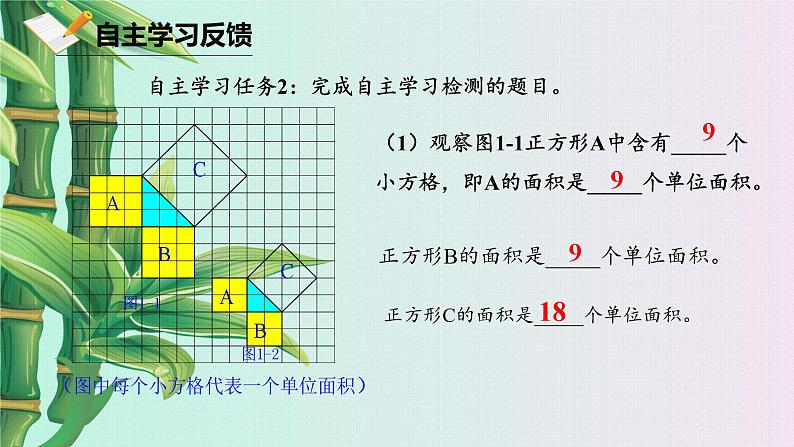
自主学习任务2：完成自主学习检测的题目。
（1）观察图1-1正方形A中含有_____个小方格，即A的面积是_____个单位面积。
正方形B的面积是_____个单位面积。
正方形C的面积是_____个单位面积。
（2）在图1-2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？
（3）你能发现两图中三个正方形A，B，C的面积S1、S2、S3之间有什么关系吗？
即：两条直角边上的正方形面积之和等于斜边上的正方形的面积。
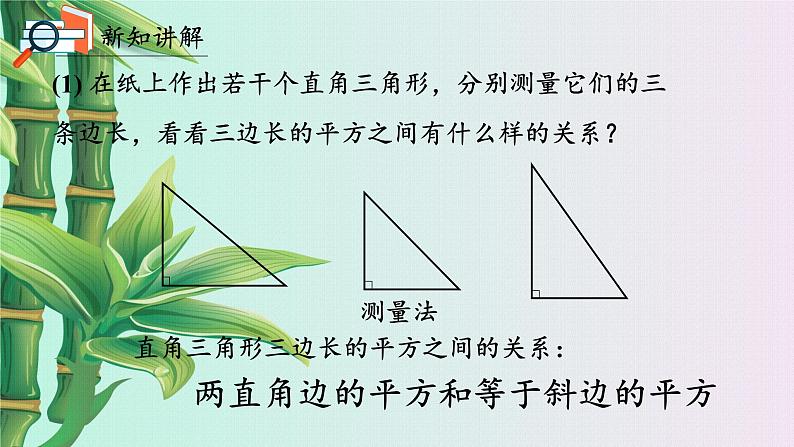
(1) 在纸上作出若干个直角三角形，分别测量它们的三条边长，看看三边长的平方之间有什么样的关系？
直角三角形三边长的平方之间的关系：
两直角边的平方和等于斜边的平方
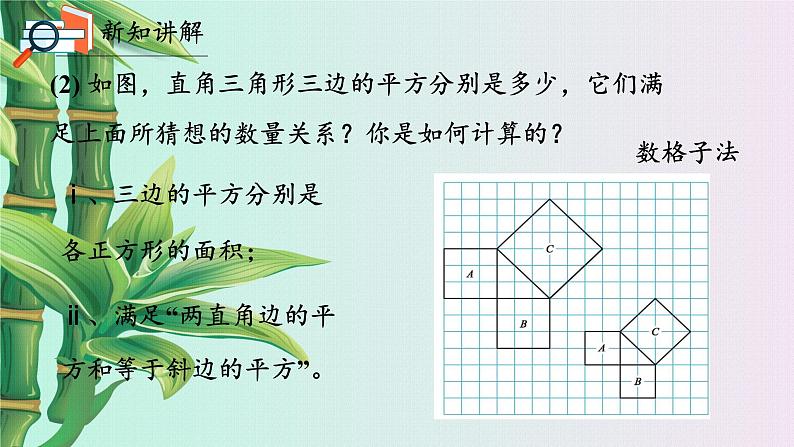
(2) 如图，直角三角形三边的平方分别是多少，它们满足上面所猜想的数量关系？你是如何计算的？
ⅰ、三边的平方分别是各正方形的面积；
ⅱ、满足“两直角边的平方和等于斜边的平方”。
一般的直角三角形,上述结论成立吗？
如果直角三角形两直角边分别为a,b,斜边为c，那么
即 直角三角形两直角边的平方和等于斜边的平方
如果直角三角形两直角边长分别为 BC=5厘米 ， AC=12厘米，求斜边AB的长度.
解：在Rt△ABC中，由勾股定理得,
AB²=AC²+BC²，
AB2=122+52.∴AB2=169.∴AB=13.答：斜边AB的长度为13厘米 .
做一做下面的题目，看谁做得又快又准确。
已知∠ACB=90°,CD⊥AB,AC=3,BC=4. 求CD的长.
归纳：已知直角三角形的两边，求第三边，是勾股定理的一个重要应用.
解：∵ ∠ACB=90°，AC=3，BC=4， ∴ AB2=AC2+BC2=25， 即AB=5. 根据三角形面积公式， ∴ AC×BC= AB×CD. ∴ CD= .
？=325 x=8
1.求下列图中字母所表示的正方形的面积
2.阴影部分是一个正方形，则此正方形的面积为_______.
3. 小明的妈妈买了一部29英寸（74厘米）的电视机.小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了.你能解释这是为什么吗？
分组探讨学习，看哪个组做得又快又准确。
一直角三角形的两边长分别是3和4，则第三边长的平方为（ ）A.25 B .7 C.5 D 25或7.
一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
解：在Rt△ABC中，根据勾股定理，得：BC2=AB2-AC2 =2.52-2.42 =0.49，所以BC=0.7.
归纳：应用勾股定理的前提是直角三角形，即只有在直角三角形中，三边才满足关系式a2+b2=c2，尤其注意斜边的确定.
一直角三角形的两边长分别是3和4，则第三边长的平方为（ ）A.25 B .7 C.5 D. 25或7
1、勾股定理：直角三角形两直角边的平方和等于斜边的平方。2、验证“勾股定理”的方法：(1)测量法(2)数格子法3、“勾股定理”的应用：已知直角三角形两边，求第三边。
1.完成八年级上册1.1.1探索勾股定理A组 课后作业。 2.预习课本4页-6页，完成1.1.2探索勾股定理自主学习检测题目。
1.完成八年级上册1.1.1探索勾股定理B组 课后作业。 2.预习课本4页-6页，完成1.1.2探索勾股定理自主学习检测题目。