北师大版九年级上册第四章 图形的相似综合与测试课时练习

这是一份北师大版九年级上册第四章 图形的相似综合与测试课时练习，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题(每小题3分，共24分)
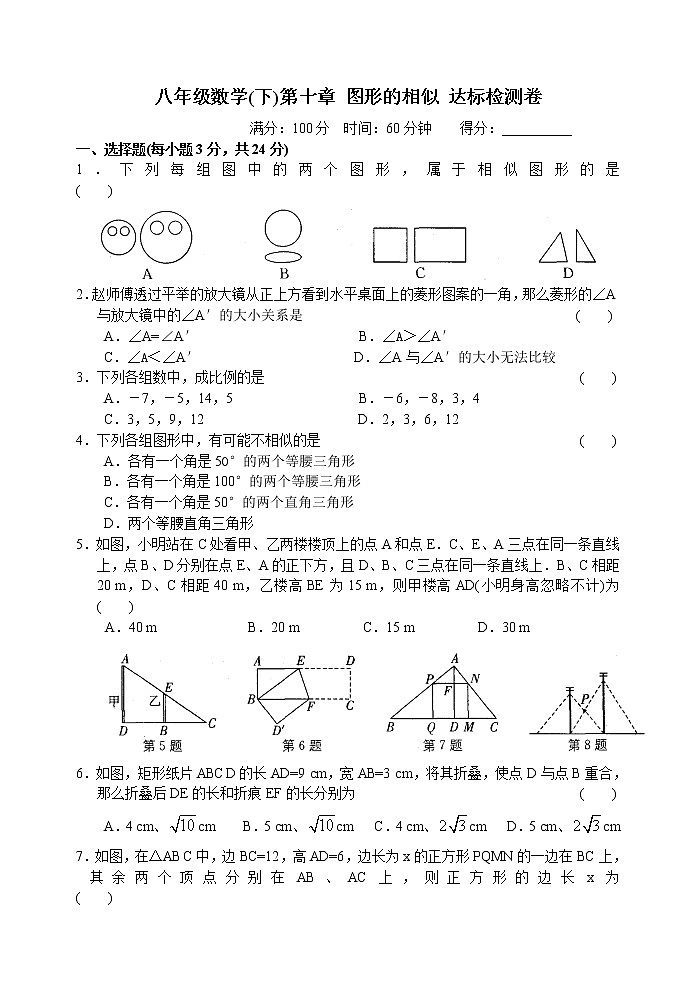
1．下列每组图中的两个图形，属于相似图形的是 ( )
2．赵师傅透过平举的放大镜从正上方看到水平桌面上的菱形图案的一角，那么菱形的∠A与放大镜中的∠A′的大小关系是 ( )
A．∠A=∠A′ B．∠A＞∠A′
C．∠A＜∠A′ D．∠A与∠A′的大小无法比较
3．下列各组数中，成比例的是 ( )
A．－7，－5，14，5 B．－6，－8，3，4
C．3，5，9，12 D．2，3，6，12
4．下列各组图形中，有可能不相似的是 ( )
A．各有一个角是50°的两个等腰三角形
B．各有一个角是100°的两个等腰三角形
C．各有一个角是50°的两个直角三角形
D．两个等腰直角三角形
5．如图，小明站在C处看甲、乙两楼楼顶上的点A和点E．C、E、A三点在同一条直线上，点B、D分别在点E、A的正下方，且D、B、C三点在同一条直线上．B、C相距20 m，D、C相距40 m，乙楼高BE为15 m，则甲楼高AD(小明身高忽略不计)为 ( )
A．40 m B．20 m C．15 m D．30 m
6．如图，矩形纸片ABCD的长AD=9 cm，宽AB=3 cm，将其折叠，使点D与点B重合，那么折叠后DE的长和折痕EF的长分别为 ( )
A．4 cm、cm B．5 cm、cm C．4 cm、cm D．5 cm、cm
7．如图，在△ABC中，边BC=12，高AD=6，边长为x的正方形PQMN的一边在BC上，
其余两个顶点分别在AB、AC上，则正方形的边长x为 ( )
A．6 B．5 C．4 D．3
8．如图，相邻两根电杆都用钢索在地面上固定，一根电杆钢索系在离地面4 m处，另一根电杆钢索系在离地面 6 m处，则中间两根钢索相交处点P离地面 ( )
A．2．4 m B．2．8 m C．3 m D．高度不能确定
二、填空题(每小题2分，共20分)
9．在一张比例尺为1：2 000的学校平面图上，操场的长度为4 cm，则此操场的实际长度为_________m．
10．设2y－3x=0(y≠0)，则=________．
11．(2009·太原)如图是一种贝壳的俯视图，点C分线段AB近似于黄金分割．已知AB=
10 cm，则AC的长约为________cm(精确到0．1 cm)．
12．已知一个三角形的三边长分别是6、10、14，与其相似的三角形的最长边是28，则这个三角形的周长等于_________．
13．在同一时刻，某人身高1．6 m，影长1 m，一塔的影长25 m，则这座塔高_______m．
14．如图，正方形ABCD的边长为2，AE=EB．MN=1，线段MN的两端在CB、CD上滑
动，当CM=________时，△AED与以N、M、C为顶点的三角形相似．
15．顶角为36°的等腰三角形称为黄金三角形．如图，△ABC、△BDC、ADEC都是黄金三角形，若AB=1，则DE≈________(保留三位有效数字)．
16．(2009·威海)如图，△ABC与△A′B′C′是位似图形，点O是位似中心，若OA=2AA′，S△ABC=8，则S△A′B′C′=________．
17．如图，三边长分别为3、4、5 的直角三角形的一个顶点与正方形的顶点B重合，另两个顶点分别在正方形的两条边AD、DC上，那么这个正方形的面积是_________．
18．兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为l m的竹竿的影长为0．4 m同时，另一名同学测量树的高度时发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0．2 m，一级台阶高为0．3 m，如图所示，若此时落在地面上的影长为4．4 m，则树高为________m．
三、解答题(共44分)
19．(8分)在△ABC中，点D、E分别在边AB、AC上，DE∥BC．若AD=4 cm，AB=6 cm，DE=3 cm，求BC的长．
20．(8分)(2008·宁夏)如图，在边长均为l的小正方形网格纸中，△OAB的顶点O、A、B均在格点上，且O是直角坐标系的原点，点A在x轴上．
(1)以O为位似中心，将△OAB放大，使得放大后的△OA1B1与△OAB对应线段的比
为2：1，画出△OA1B1 (所画△OA1B1与△OAB在原点两侧)．
(2)求出线段A，B，所在直线的函数关系式．
21．(8分)学生会举办一个校园摄影艺术展览会，小华和小刚准备将矩形的作品四周镶上
一圈等宽的纸边，如图所示．两人在设计时发生了争执：小华要使内外两个矩形相似，
认为这样视觉效果较好；小刚试了几次不能办到，表示这是不可能的．小红和小莉了解情况后，红说这一要求只有当矩形是黄金矩形时才能做到，小莉则坚持只有当矩形
是正方形时才能做到．请你动手试一试，说一说你的看法．
22．(10分)如图，四边形ABCD是平行四边形，点F在BA的延长线上，连接CF交AD于点E
(1)试说明：△CDE∽△FAE．
(2)当E是AD的中点，且BC=2CD时，试说明：∠F=∠BCF．
23．(10分)马戏团让狮子和公鸡表演跷跷板节目．跷跷板支柱AB的高度为1．2米．
(1)若吊环高度为2米，支点A为跷跷板PQ的中点，狮子能否将公鸡送到吊环上?为
什么?
(2)若吊环高度为3．6米，在不改变其他条件的前提下移动支柱，当支点A移到跷跷
板PQ的什么位置时，狮子刚好能将公鸡送到吊环上?
24．(12分)善于学习的小敏查资料知道：对应角相等、对应边成比例的两个梯形，叫做相似梯形．他想到“平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似”，提出如下两个问题，你能帮助解决吗?
问题一 平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似?
(1)从特殊情形人手探究．假设在梯形ABCD中，AD∥BC，AB=6，BC=8，CD=4，
AD=2，MN是中位线[如图(1)所示]．根据相似梯形的定义，请你说明梯形
AMND与梯形ABCD是否相似?
(2)一般结论：平行于梯形底边的直线截两腰所得的梯形与原梯形________(填“相似”
或“不相似”或“相似性无法确定”)．
问题二 平行于梯形底边的直线截两腰所得的两个小梯形是否相似?
(3)从特殊平行线入手探究．梯形的中位线截两腰所得的两个小梯形________(填“相
似”或“不相似”或“相似性无法确定”)．
(4)从特殊梯形人手探究．同上假设，在梯形ABCD中，AD∥BC，AB=6，BC=8，CD
=4，AD=2，你能找到与梯形底边平行的直线PQ[点P、Q在梯形的两腰上，如图
(2)所示]，使得梯形APQD与梯形PBCQ相似吗?请根据相似梯形的定义说明
理由．
(5)一般结论：对于任意梯形[如图(3)所示]，一定_______(填“存在”或“不存在”)平行于梯形底边的直线PQ，使截得的两个小梯形相似．若存在，则确定这条平行线位置的条件是=________(不妨设AD=a，BC=b，AB=c，CD=d)．
参考答案
1．A 2．A 3．B 4．A 5．D 6．B 7．C 8．A 9．80 10． 11．6．2 12．54 13．60 14．或 15．0．382 16．18 17． 18．11．8
19．BC=4．5 cm 20．(1)图略 (2)由题意，得A1 (4，0)、B1 (2，－4)．设线段A1B1所在直线的函数关系式为y=kx+b(k≠0)．得．解得所以函数关系式为y=2x－8 21．只有是正方形时才能做到．设矩形的一边为a，另一边为b，等宽的纸边宽c．按照小华的要求，得．化简，得a=b，即该矩形是正方形
22．(1)因为四边形ABCD是平行四边形，所以AB∥CD．所以∠F=∠DCE，∠EAF=∠D．所以△CDE∽△FAE (2)因为E是AD的中点，所以DE=AE．由(1)得．所以CD=AF．因为四边形ABCD是平行四边形，所以AB=CD．所以AB=CD=A F．所以BF=2CD．又因为BC=2CD，所以BC=BF．所以∠F=∠BCF
23．(1)狮子能将公鸡送到吊环上．如图，当狮子将跷跷板P端按到底时可得到Rt△PHQ．因为AB为△PHQ的中位线，AB=1．2米，所以QH=2．4米＞2米
(2)支点A移到跷跷板PQ的三分之一处(即)时，狮子刚好能将公鸡送到吊环上．因为△PAB∽△PQH，，所以QH=3AB=3．6(米) 24．(1)因为MN是中位线，所以，．显然对应边不成比例，所以梯形AMND与梯形ABCD不相似 (2)不相似 (3)不相似 (4)如果梯形APQD与梯形PBCQ相似，则，即．解得PQ=4．此时．又因为AB=6，所以AP≈2．即当AP=2，且PQ∥BC时，．又因为两梯形对应角相等，所以梯形APQD与梯形PBCQ相似 (5)存在