初中数学青岛版八年级上册2.2 轴对称的基本性质教学设计

这是一份初中数学青岛版八年级上册2.2 轴对称的基本性质教学设计，共3页。教案主要包含了教学目标，教学重难点，教学过程等内容，欢迎下载使用。

【教学目标】
1．经历“探索轴对称图形的性质”的过程，理解“连接对应点的线段被对称轴垂直平分、对应线段相等、对应角相等”的性质。
2．会画出与已知图形关于某条直线对称的图形。
3．发展学生合作交流的能力和数学表达能力。
【教学重难点】
轴对称的基本性质的理解与运用。
【教学过程】
1．实验与探究
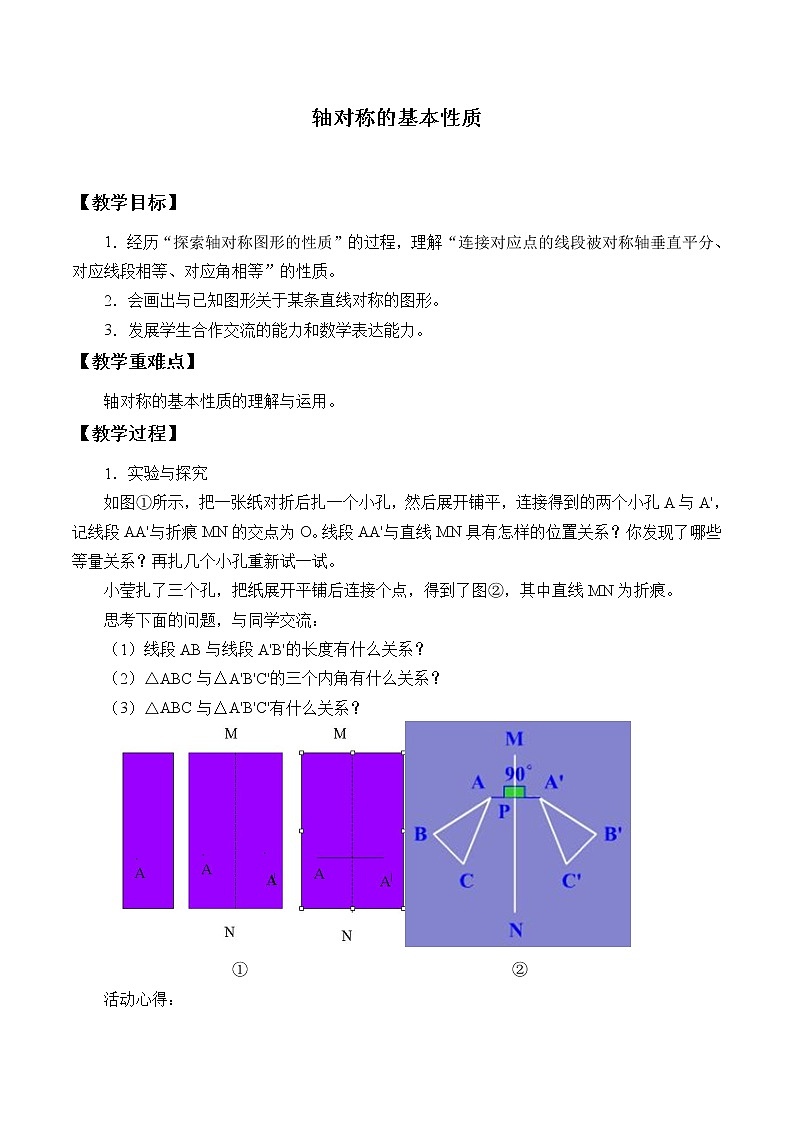
如图①所示，把一张纸对折后扎一个小孔，然后展开铺平，连接得到的两个小孔A与A'，记线段AA'与折痕MN的交点为O。线段AA'与直线MN具有怎样的位置关系？你发现了哪些等量关系？再扎几个小孔重新试一试。
小莹扎了三个孔，把纸展开平铺后连接个点，得到了图②，其中直线MN为折痕。
思考下面的问题，与同学交流：
（1）线段AB与线段A'B'的长度有什么关系？
（2）△ABC与△A'B'C'的三个内角有什么关系？
（3）△ABC与△A'B'C'有什么关系？
① ②
活动心得：
轴对称的基本性质：如果两个图形关于某一条直线成轴对称，那么连接对应点的线段被对称轴垂直平分；对应线段相等，对应角相等。
2．例题1讲解（补充）
如图：两个三角形关于直线L成轴对称，如果三角形的部分边长（单位：厘米）和角的度数如图所示，求未知的边长和度数。
解：因为这两个三角形关于直线L成轴对称，他们的对应角相等、对应线段相等，所以：
a=3.20厘米，b=3.44厘米，c=2.29厘米；
∠α=75°，∠r=43°
又因为三角形的内角和为180°，所以：
∠δ=∠β=180°－75°－43°=62°
3．跟踪练习
（1）把例题中的三角形的顶点分别用字母表示出来，连接对应顶点，指出哪些线段被直线L垂直平分。
（2）如图，△ABC与△A'B'C'关于直线MN成轴对称，指出三对对应点、对应线段和对应角，并找出三对相等的线段和相等的角。
4．交流与发现
如图：在纸上画一条直线MN，再在直线MN的一侧扎一个小孔（点A），不用折纸的方法你能找到小孔（点A）关于直线MN的对称点A'的位置吗？与同学交流。
如图：过点A作直线MN的垂线EF，设垂足为O。
在射线OF上截取OA'等于OA。
点A'就是点A关于直线MN的对称点。
5．例题2讲解
如图：做出△BCD关于直线L的对称图形。
解：如上图，分别作出点B、C、D三点关于直线L的对称点B'、C'、D'，顺次连接B'、C'、D'三点，△B'C'D就是所求作的图形。
归纳总结：
画一个多边形关于某条直线的轴对称图形时，可以先分别画出已知多边形的各个顶点关于这条直线的对应点；然后再顺次连接它们，便可得到多边形关于这条直线的对称图形。
6．课堂小结
本节课主要学习轴对称图形的性质，及利用该性质解题。