初中数学人教版九年级上册第二十五章 概率初步25.1 随机事件与概率25.1.2 概率备课课件ppt

这是一份初中数学人教版九年级上册第二十五章 概率初步25.1 随机事件与概率25.1.2 概率备课课件ppt，共38页。PPT课件主要包含了用什么方法求概率，列举的方法，1直接列举法，2“列表”法，3“树形图”法，画树形图如下，硬币1，硬币2，硬币3，用列举法求概率等内容，欢迎下载使用。
2、等可能事件概率公式：
(1)所有可能结果是有限个；
3、求等可能事件概率的条件：
(2)每种结果的可能性都相等。
1.概率的定义，事件的分类
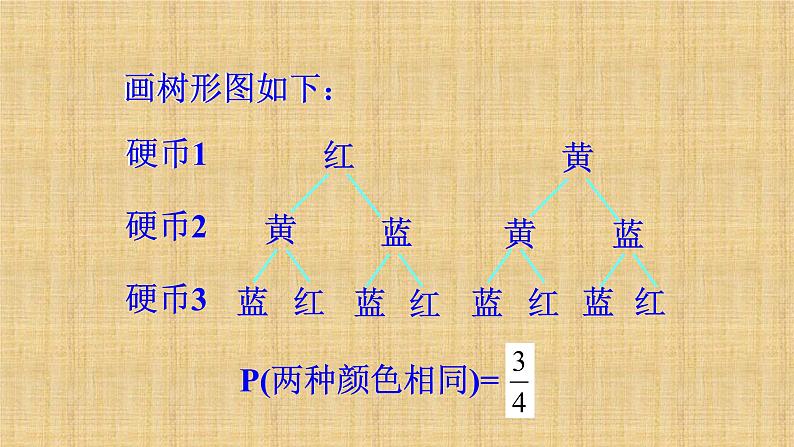
有三枚硬币，硬币1的一面涂有红色，另一面涂有黄色；硬币2的一面涂有黄色，另一面涂有蓝色；硬币3的一面涂有蓝色，另一面涂有红色。现将这三枚硬币随意抛出，求两枚的颜色相同的概率。
事件结果显而易见，可能性较少；
事件结果较复杂，可能性较多；
事件结果较复杂，步骤较多。
用列举法求概率的条件是什么?
(1)实验的所有结果是有限个(n)(2)各种结果的可能性相等.
如图，有一枚质地均匀的硬币，将它抛出后，你知道正面朝上的概率吗？
(1)是不是等可能事件？
(2)用什么方法求概率？
所有可能结果是有限个；
每种结果的可能性都相等。
投掷一枚硬币，“正面向上”
能否理解为：“投掷2次，1次正面向上”；“投掷100次，50次正面向上”；“投掷n次，n/2次正面向上”……
投掷一枚硬币，“正面向上”的频率
例如，历史上曾有人做过抛掷硬币的大量重复试验，结果如下表 ：
当重复抛掷一枚硬币时，“正面向上”的频率在0.5左右摆动。随着抛掷次数的增加，一般地频率呈现出一定的稳定性：在0.5左右摆动的幅度会越来越小。我们称
用列举法可以求一些事件概率，还可以利用多次重复试验，通过统计实验结果去估计概率
则估计油菜籽发芽的概率为＿＿＿
如图，有一枚图钉，将它抛出后，要考察钉尖的朝向上的概率。
(1)钉尖的朝向有几种可能的结果？
(2)这两种结果可能性相等吗？
这两种结果可能性不相等。
　　在长期的实践中，人们观察大数法则,亦称大数定律.即：在相同的条件下，做大量的重复实验时，根据一个随机事件发生的频率所逐渐稳定的常数，可以估计这个事件发生的概率。
由频率可以估计概率是由瑞士数学家雅各布·伯努利（1654－1705）最早阐明的，因而他被公认为是概率论的先驱之一．
对一般的随机事件，在做大量重复试验时，一个事件出现的频率，总是在某个常数附近摆动，显示出一定的稳定性.
一般地，在大量重复试验中，如果事件发生的频率（m/n）会稳定在某个常数 p 附近，那么，事件发生的概率为 p.
需要注意的是:概率是针对大量重复的试验而言的,大量试验反映的规律并非在每一次试验中出现.
更一般地,即使试验的所有可能的结果不是有限个,或各种可能的结果发生的可能性不相等,也可以通过试验的方法去估计一个随机事件发生的概率.只要试验次数是足够大的,频率 就可以作为概率p的估计值.
区别：1频率反映事件发生的频繁程度； 概率反映事件发生的可能性大小. 2 频率是不能脱离具体的n次试验的结果，具有随机性；概率是具有确定性的不依赖于试验次数的理论值.联系：频率是概率的近似值，概率是频率的稳定值.
用频率估计概率的基本步骤：
1． 大量重复试验2． 检验频率是否已表现出稳定性3． 频率的稳定值即为概率
注：(1)求一个事件的概率的基本方法是通过大量的重复试验；(2)只有当频率在某个常数附近摆动时，这个常数才叫做事件A的概率；(3)概率是频率的稳定值，而频率是概率的近似值；(4)概率反映了随机事件发生的可能性的大小；(5)必然事件的概率为1，不可能事件的概率为0．因此0P(A)1
1 天气预报的概率解释
（1）天气预报是气象专家依据观察到的气象资料和专家们的实际经验，经过分析推断得到的。它是主观概率的一种，而不是本书上定义的概率。
（2）降水概率 的大小只能说明降水可能性的大小，概率值越大只能表示在一次试验中发生可能性越大，并不能保证本次一定发生。
天气预报说下星期一降水概率是90%，下星期三降水概率是10%，于是有位同学说：下星期一肯定下雨，下星期三肯定不下雨。你认为他说的对吗？
不对。所谓降水概率90%、10%是在大量的统计记录的条件下，那么它是符合大多数同等天气条件下的实际情况的，但某些例外也还是可能的。
2 某射手进行射击，结果如下表所示：
(2)这个射手射击一次，击中靶心的概率是多少？
(3)这射手射击1600次，击中靶心的次数约是　　。
3：有人说，既然抛掷一枚硬币出现正面的为，那么连续两次抛掷一枚质地均匀的硬币，一定是一次正面朝上，一次反面朝上，你认为这种想法正确吗？
答：这种说法是错误的，抛掷一枚硬币出现正面的概率为，它是大量试验得出的一种规律性结果，对具体的几次试验来讲不一定能体现出这种规律性，在连续抛掷一枚硬币两次的试验中，可能两次均正面向上，也可能两次均反面向上，也可能一次正面向上，一次反面向上
问题1 某厂打算生产一种中学生使用的笔袋，但无法确定各种颜色的产量.你认为该如何制定生产计划？
针对中学生喜欢的颜色的问题，小凯调查了九年级某班50位同学，结果如下：
你认为小凯的调查能反映所有九年级同学对文具颜色的喜好吗？
为了更为准确地为文具厂商提供信息，你认为抽样调查应注意什么？
抽样调查应更广泛、更有代表性、更有随意性.
问题2 该文具厂就该笔袋的颜色随机调查了5 000名中学生，并在调查到1 000名、2 000名、3 000名、4 000名、5 000名时分别计算了各种颜色的频率，绘制折线图如下：
某厂打算生产一种中学生使用的笔袋，但无法确定各种颜色的产量，于是该文具厂就笔袋的颜色随机调查了5 000名中学生，并在调查到1 000名、2 000名、3 000名、4 000名、5 000名时分别计算了各种颜色的频率，绘制折线图如下：
(1)随着调查次数的增加，红色的频率如何变化？
(2)你能估计调查到10 000名同学时，红色的频率是多少吗？
估计调查到10 000名同学时，红色的频率大约仍是40%左右.
随着调查次数的增加，红色的频率基本稳定在40%左右.
(3)若你是该厂的负责人,你将如何安排生产各种颜色的产量？
红、黄、蓝、绿及其它颜色的生产比例大约为4:2:1:1:2 .
（1）试验的次数越多，所得的频率越能反映概率的大小； （2）频数分布表、扇形图、条形图、直方图都能较好地反映频数、频率的分布情况，我们可以利用它们所提供的信息估计概率．
（3）当试验次数很大时,一个事件发生频率也稳定在相应的概率附近.因此,我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.
（4） 在相同情况下随机的抽取若干个体进行实验,进行实验统计.并计算事件发生的频率 根据频率估计该事件发生的概率.
1. 概率的获取有 和 两种。
2. 本节课的事件概率无法用理论计算来解决，只能通过概率实验，用 来估算。
本节课主要学习了用频率估计概率，记住：只要试验次数是足够大的,频率就可以作为概率的估计值.
了解了一种方法-------用多次试验频率去估计概率
用样本去估计总体用频率去估计概率
弄清了一种关系------频率与概率的关系
　　当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.
结束寄语: 概率是对随机现象的一种数学描述,它可以帮助我们更好地认识随机现象,并对生活中的一些不确定情况作出自己的决策. 从表面上看，随机现象的每一次观察结果都是偶然的，但多次观察某个随机现象，立即可以发现：在大量的偶然之中存在着必然的规律.
1.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾，一渔民通过多次捕获实验后发现：鲤鱼、鲫鱼出现的频率是31%和42%，则这个水塘里有鲤鱼_______尾,鲢鱼_______尾.
2.动物学家通过大量的调查估计出，某种动物活到20岁
的概率为，活到25岁的概率是，活到30岁的概率
是0.3.现年20岁的这种动物活到25岁的概率为多少？现
年25岁的这种动物活到30岁的概率为多少？
3.在有一个10万人的小镇,随机调查了2000人,其中有250人看中央电视台的早间新闻.在该镇随便问一个人,他看早间新闻的概率大约是多少?该镇看中央电视台早间新闻的大约是多少人?
解: 根据概率的意义,可以认为其概率大约等于250/2000=. 该镇约有100000×0.125=12500人看中央电视台的早间新闻.
4.一个口袋中放有20个球,其中红球6个,白球和黑球各若干个,每个球出了颜色外没有任何区别.(1)小王通过大量反复实验(每次取一个球,放回搅匀后再取)发现,取出黑球的概率稳定在1/4左右,请你估计袋中黑球的个数.(2)若小王取出的第一个是白球,将它放在桌上,从袋中余下的球中在再任意取一个球,取出红球的概率是多少?
5　从一定的高度落下的图钉，落地后可能图钉尖着地，也可能图钉尖不找地，估计一下哪种事件的概率更大，与同学合作，通过做实验来验证 一下你事先估计是否正确？
你能估计图钉尖朝上的概率吗？
6 如图,长方形内有一不规则区域,现在玩投掷游戏,如果随机掷中长方形的300次中，有100次是落在不规则图形内.
(1)你能估计出掷中不规则图形的概率吗？
(2)若该长方形的面积为150,试估计不规则图形的面积.
7小红和小明在操场上做游戏，他们先在地上画了半径分别为2m和3m的同心圆(如图)，蒙上眼在一定距离外向圈内掷小石子，掷中阴影小红胜，掷中里面小圈小明胜，未掷入大圈内不算，你认为游戏公平吗？为什么？
8 某篮球运动员在最近的几场大赛中罚球投篮的结果如下：
(1)计算表中各次比赛进球的频率；
(2)这位运动员投篮一次，进球的概率约为多少？