河北省保定市第二十八中学2020-2021学年高一下学期五月月考数学试题+Word版含答案

这是一份河北省保定市第二十八中学2020-2021学年高一下学期五月月考数学试题+Word版含答案，共10页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

1．设复数满足，则（ ）
A．B．C．D．
2．已知空间向量，，若，则实数的值是（ ）
A．-1B．0C．1D．2
3．某中学春季运动会上，12位参加跳高半决赛同学的成绩各不相同，按成绩从高到低取前6位进入决赛．如果小明知道了自己的成绩后，则他可根据其他11位同学成绩的哪个数据判断自己能否进入决赛（ ）
A．中位数B．平均数C．极差D．方差
4．从装有两个红球和两个黑球的口袋内任取两个球，那么互斥而不对立的事件是（ ）
A．至少有一个黑球与都是黑球B．至少有一个黑球与至少一个红球
C．至少有一个黑球与都是红球D．恰好有一个黑球与都是红球
5．唐朝的狩猎景象浮雕银杯如图1所示，其浮雕临摹了国画、漆绘和墓室壁画，体现了古人的智慧与工艺．它的盛酒部分可以近似地看作是半球与圆柱的组合体（假设内壁表面光滑，忽略杯壁厚度）如图2所示，设酒杯上部分（圆柱）的体积为，下部分（半球）的体积为，若，则半球的半径与圆柱的高之比为（ ）
AB．C．D．
6．已知，是非零向量且满足，，则的形状为（ ）
A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形
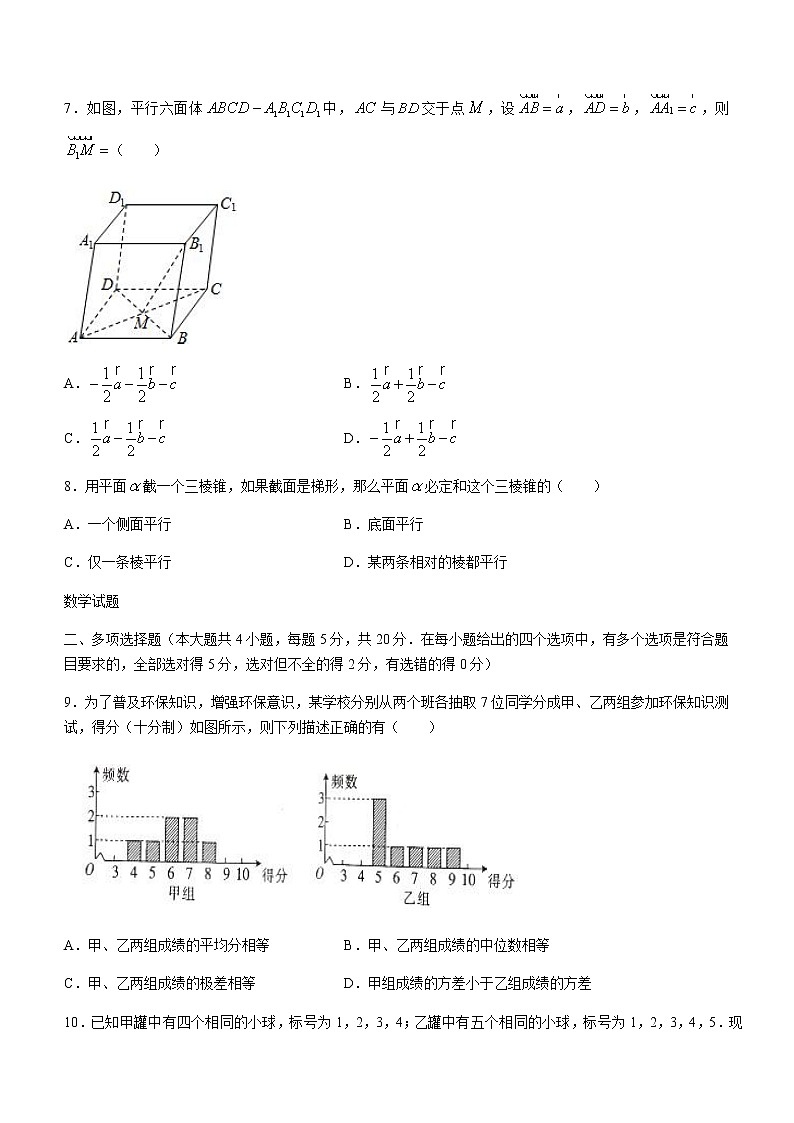
7．如图，平行六面体中，与交于点，设，，，则（ ）
A．B．
C．D．
8．用平面截一个三棱锥，如果截面是梯形，那么平面必定和这个三棱锥的（ ）
A．一个侧面平行B．底面平行
C．仅一条棱平行D．某两条相对的棱都平行
数学试题
二、多项选择题（本大题共4小题，每题5分，共20分．在每小题给出的四个选项中，有多个选项是符合题目要求的，全部选对得5分，选对但不全的得2分，有选错的得0分）
9．为了普及环保知识，增强环保意识，某学校分别从两个班各抽取7位同学分成甲、乙两组参加环保知识测试，得分（十分制）如图所示，则下列描述正确的有（ ）
A．甲、乙两组成绩的平均分相等B．甲、乙两组成绩的中位数相等
C．甲、乙两组成绩的极差相等D．甲组成绩的方差小于乙组成绩的方差
10．已知甲罐中有四个相同的小球，标号为1，2，3，4；乙罐中有五个相同的小球，标号为1，2，3，4，5．现从甲罐、乙罐中分别随机抽取1个小球，记事件“抽取的两个小球标号之和大于5”，事件“抽取的两个小球标号之积大于8”，则（ ）
A．从甲罐中抽到标号为2的小球的概率为
B．事件发生的概率为
C．事件发生的概率为
D．事件发生的概率为
11．某市教体局对全市高三年级的学生身高进行抽样调查，随机抽取了100名学生，他们的身高都处在，，，，五个层内，根据抽样结果得到统计图表，则下面叙述正确的是（ ）
A．样本中女生人数多于男生人数B．样本中层人数最多
C．样本中层次男生人数为6人D．样本中层次男生人数多于女生人数
12．如图，在正方体中，点是棱上的一个动点，给出以下结论，其中正确的有（ ）
A．与所成的角为45°
B．平面
C．平面平面
D．对于任意的点，三棱锥的体积均不变
三、填空题（本大题共4小题，每小题5分，共20分．把答案填在题中横线上）
13．已知复数在复平面内对应的点在第三象限，则实数的取值范围是______．
14．某健康协会从某地区睡前看手机的居民中随机选取了270人进行调查，得到如图所示的频率分布直方图，则可以估计睡前看手机在40~50分钟的人数为______．
15．甲、乙两队进行篮球决赛，采取三场二胜制（当一队赢得二场胜利时，该队获胜，决赛结束）．根据前期比赛成绩，甲队的主客场安排依次为“主客主”．设甲队主场取胜的概率为0.6，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以获胜的概率是______．
16．在三棱柱中，为侧棱的中点，从该三棱柱的九条棱中随机选取两条，则这两条棱所在直线至少有一条与直线异面的概率是______．
四、解答题（6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤）
17．（10分）
在棱长是2的正方体中，，，分别为，，的中点．应用空间向量方法求解下列问题．
（1）求的长．
（2）求异面直线与所成角的余弦值．
18．（12分）为了了解我市参加2018年全国高中数学联赛的学生考试结果情况，从中选取60名同学将其成绩（百分制，均为正数）分成，，，，，六组后，得到部分频率分布直方图（如图），观察图形，回答下列问题：
（1）求分数在内的频率，并补全这个频率分布直方图；
（2）根据频率分布直方图，估计本次考试成绩的众数、平均数；
（3）根据评奖规则，排名靠前10%的同学可以获奖，请你估计获奖的同学至少需要所少分?
19．（12分）
在①，②，③，这三个条件中任选一个，补充在下面问题的横线上，并解决该问题．
（如果选择多个条件分别解答，按第一个解答给分）
已知的内角，，的对边分别为，，，______，，．
（1）求角；
（2）求的面积．
20．（12分）
已知某区甲、乙、丙三所学校的教师志愿者人数分别为240，160，80．为助力疫情防控，现采用按比例分配分层抽样的方法，从这三所学校的教师志愿者中抽取6名教师，参与“抗击疫情·你我同行”下卡口执勤值守专项行动．
（1）求应从甲、乙、丙三所学校的教师志愿者中分别抽取的人数；
（2）设抽出的6名教师志愿者分别记为，，，，，，现从中随机抽取2名教师志愿者承担测试体温工作．
①写出本次实验的样本空间；
②设为事件“抽取的2名教师志愿者来自同一所学校”，求事件发生的概率．
21．（12分）
如图，四棱锥中，底面为菱形，平面，为的中点．
（1）求证：平面；
（2）求证：平面平面；
（3）当，时，求三棱锥的体积．
22．（12分）
如图，在三棱锥中，，，，，，为线段的中点，为线段上一点．
（1）求证：；
（2）求证：平面平面；
（3）当P平面时，求直线与平面所成的角．
高一5月考试数学试题答案及评分标准：
1-8：ACADBADC9-12：BCDBDABC
13．（或）14．8115．0.316．
18．（1）0.25图中长方形高度0.025
（2）由图知，众数为：75和85
平均数为：．
（3）因为分数在内的频率为0.25，内的频率为0.05，
而所以得分前10%的分界点应在80至90之间．
设所求的分界点为，则，解得
所以得分前10%的分界点为88，即获奖的同学至少需要88分．
19．解：（1）若选择①，，
由余弦定理得，因为，所以；
若选择②，，则，
因为，所以，因为，所以；
若选择③，，
则，所以，
因为，所以，所以，所以．
（2）由正弦定理，得，
因为，，所以，
所以，
所以．
21．（1）取、中点为，连接．
证明：底面为菱形且为、的交点
为中点．
为中点
．
平面，平面，
平面．
（2）底面为菱形，
．
平面
．
平面．
平面．
平面平面．
（3），
，．
22．（1）证明：，，且，
平面，
又平面，
．
（2）证明：，，
．
平面
，
而，
平面，
平面，
平面平面．
（3）解：平面，且平面，平面平面，
．
平面，
平面，
为直线与平面所成的角．
在中，，．
则，所以，
即直线与平面所成角为．