

广西南宁市第三中学、北海中学2020-2021学年高一下学期6月联考数学试题+Word版含答案
展开这是一份广西南宁市第三中学、北海中学2020-2021学年高一下学期6月联考数学试题+Word版含答案,共14页。试卷主要包含了选择题, 填空题, 解答题等内容,欢迎下载使用。
南宁三中 北海中学 2020级高一6月联考
数学试题
一、选择题 (本题共12小题,每小题有且仅有一个正确答案,每小题 5 分 ,共60分)
1.下列命题正确的是( )
A.铺得很平的一张纸是一个平面 B.四边形一定是平面图形
C.三点确定一个平面 D.梯形可以确定一个平面
2.已知向量,,若,则实数m的值为( )
A.4 B. C.1 D.
3.的值是( )
A. B. C. D.
4.由首项a1=1,公比q=2确定的等比数列{an}中,当an=64时,序号n等于( )
A.4 B.5 C.6 D.7
5.某圆锥的侧面展开图是面积为且圆心角为的扇形,则此圆锥的体积为( )
A. B. C. D.
6.当时,若,则的值为( )
A. B. C. D.
7.已知一个几何体的三视图如图所示,则该几何体的体积是( )
A. B.
C. D.8
8.已知变量,满足约束条件则的最大值为( )
A. B.1 C. D.
9.三棱锥中,平面ABC,,则三棱锥外接球的表面积为( )
A. B. C. D.
10.已知直三棱柱中,,,且直线A1B与平面ABC所成的角为,D为的中点,则异面直线与AD所成角的余弦值为( )
A. B. C. D.
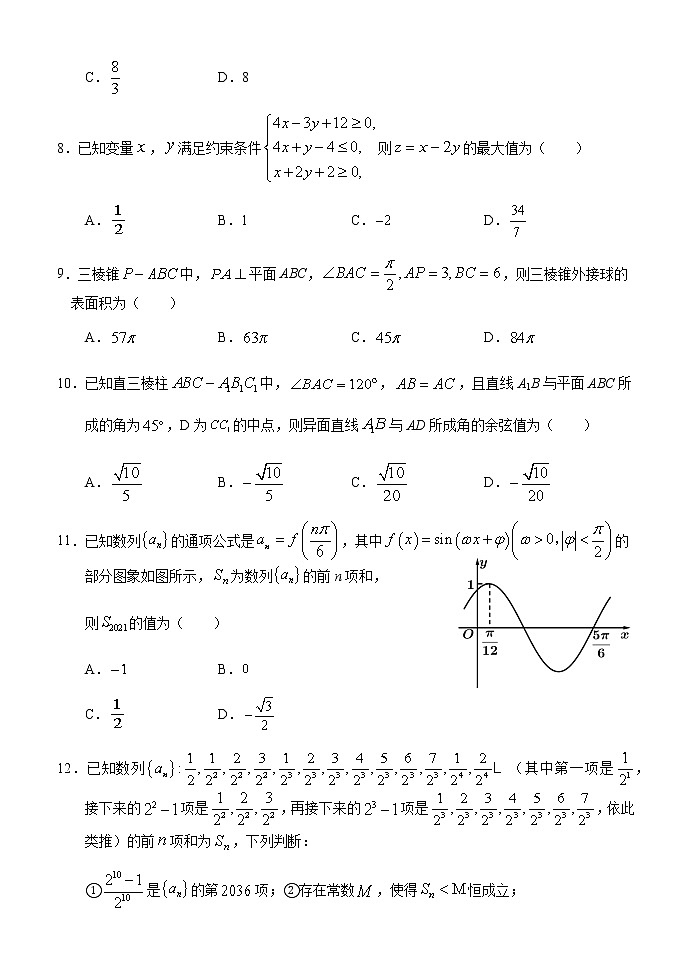
11.已知数列的通项公式是,其中的部分图象如图所示,为数列的前n项和,
则的值为( )
A. B.
C. D.
12.已知数列(其中第一项是,接下来的项是,再接下来的项是,依此类推)的前项和为,下列判断:
①是的第项;②存在常数,使得恒成立;
③; ④满足不等式的正整数的最小值是.
其中正确的序号是( )
A.①③ B.①④ C.①③④ D.②③④
二、 填空题(本题共4小题,每小题 5分,共20分 )
13.在中,边所对的角分别为,若,则______.
14.函数的定义域是,则实数的取值范围是________.
15.已知等差数列,正整数,,,满足,则的取值范围是___________.
16.给出下列说法:
①和直线都相交的两条直线在同一个平面内;
②三条两两相交的直线一定在同一个平面内;
③有三个不同公共点的两个平面重合;
④两两相交且不过同一点的四条直线共面.
其中正确说法的序号是______ .
三、 解答题 (本题共 6 小题,共70分)
17.(本小题满分10分)记为等差数列的前项和,已知,.
(1)求公差及的通项公式;
(2)求,并求的最小值.
18.(本小题满分12分)已知向量,,函数.
(1)求函数的单调增区间;
(2)当时,恒成立,求实数的取值范围.
19.(本小题满分12分)在正方体中,是棱的中点.
(1)求证:平面;
(2)若是棱的中点,求证:平面平面.
20.(本小题满分12分)在三棱锥中,,,是线段的中点,是线段的中点.
(1)求证:平面;
(2)求直线与平面所成的角的正弦值.
21.(本小题满分12分)在中,角对应边分别为,若.
(1)求角;
(2)若,求的取值范围.
22.(本小题满分12分)已知数列,满足,为数列的前项和,记的前项和为,的前项积为,且.
(1)若,求数列的通项公式;
(2)若,对任意自然数,都有,求实数的取值范围.
南宁三中 北海中学 2020级高一6月联考
数学试题答案
1.D A:平面是一个无限延展的面,而一张纸只是平面图形,错误;B:若四个顶点不共面,四边形不是平面图形,错误;C:三点共线时有无数个平面,错误;D:梯形是一个平面图形,故可以确定一个平面,正确.
2.B 解:因为,所以,解得:.
3.D
.
4.D 因为数列{an}为等比数列,所以an=a1·qn-1=2n-1=64,解得n=7.
5.B 设圆锥底面的半径为,母线长为,则侧面展开图的面积为,则,
又因为圆心角为,所以,解得 ,所以圆锥的高为,故圆锥的体积为.
6.B ∵∴∵,
∴,∴.
7.C 由给定的三视图知,这个几何体是四棱锥P-ABCD,底面ABCD是边长为2的正方形,且PA⊥平面ABCD,如图:四棱锥P-ABCD的高PA=2,底面ABCD面积为S=AB2=4,则该几何体体积为.
8.D 不等式组表示的平面区域如图中阴影部分所示(包括边界).作出直线并平移,数形结合可知当平移后的直线经过点时取得最大值.由得故,所以.
9.C 因为,所以的外接圆的半径3,其外接圆的圆心为其斜边的中点,三棱锥中,平面ABC,所以,作平面,并且取,所以点是三棱锥的外接球的球心,连结,则,所以三棱锥外接球的表面积为.
10.A因为三棱柱是直三棱柱,则平面,所以即为直线A1B与平面ABC所成的角,所以,所以, 取中点,中点,连接,则,,所以或其补角即为异面直线与AD所成角,设,则,,在中, , 在中,,,∴,因为异面直线所成的角为锐角或直角,所以异面直线与AD所成角的余弦值为 .
11.D 观察图象知:函数周期为T,,,又,而,则,所以,,数列是周期数列,周期为6,其前6项依次为,则,,则.
12.B由题意可知,数列的规律为:分母为的项有项,将数列中的项排成数阵,且使得第行每项的分母为,该行有项,如图所示,
对于命题①,位于数阵第行最后一项,对应于数列的项数为,命题①正确;对于命题②,数阵中第行各项之和为,则,且数列的前项之和为,当时,,因此,不存在正数,使得,命题②错误;对于命题③,易知第行最后一项位于数列的项数为,第行最后一项位于数列的项数为,且,则位于数阵第行第项(即),所以
,命题③错误;由①知 ,,且,则恰好满足的项位于第行,假设位于第项,则有,可得出,由于,,则,,因此,满足的最小正整数,命题④正确.
13. ,,,
,又,所以,,,,,,.
14.[0,+∞) 因为函数的定义域是,当m=0时,符合题意;当m≠0时,由题意知mx2-2mx+m+2≥0对x∈R恒成立,则, 解得m>0.综上,m≥0.所以实数的取值范围是[0,+∞).
15. 由为等差数列,且,则,所以,当且仅当时,取等号,又,所以,即,所以,故的取值范围是.
16.④ 如图,在正方体中,,,但是 异面,故①错误.又交于点,但不共面,故②错误.如果两个平面有3个不同公共点,且它们共线,则这两个平面可以相交,故③错误.如图,因为,故共面于,因为,故,故即,而,故,故即即共面,故④正确.
17.(1)设的公差为,由题意得.由得.
所以的通项公式为.(5分)
(2)由(1)得.所以时取得最小值,最小值为. (10分)
18.(1)
(3分)
由,得
∴的单调增区间是(6分)
(2)由(1)知在上单调递增,
∴当时,;当时,.(10分)
由题设可得解得,∴的取值范围是(12分)
19.(1)连,使,连.(1分)
∵是正方形,,.
又是中点,,(4分),
又平面,平面,∴平面. (6分)
(2)∵是棱的中点,是棱的中点,
且,所以四边形是平行四边形(8分)
,又平面,平面,平面. (10分)
由(1)平面,又,∴平面//平面. (12分)
20.(1)由,,有,从而有,且.
又是边长等于的等边三角形,
(2分),.
又,从而有,
,.(4分)
又,平面.(6分)
(2)过点作交于点,连.由(1)知平面,得,
又,平面,是直线与平面所成的角.(9分)
由(1)证,从而为线段的中点,,
,,
直线与平面所成的角的正弦值是.(12分)
21.解:(1)∵,
∴由正弦定理可得,(2分)
∴,∴,
∴,∵,∴,∴;(6分)
(2)由题意:,∴由余弦定理(8分)
则3(当且仅当时取等号),即,
∴.∵,∴.(12分)
22.解:(1)∵,(2分)
.∵,∴,(4分)
∵,∴.(5分)
∵,∴,∴.(6分)
(2)∵,,∴.∵,
∴,∴,∴,.(8分)
∵
两边同乘以(时,),
∴条件不等式等价于(10分),
∴当n为偶数时,恒成立,当时,,故;
当 n为奇数时,恒成立,当时,,故;
故.(12分)
相关试卷
这是一份2020-2021学年广西南宁市第三中学高一上学期月考(一)数学试题(解析版),共14页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年广西南宁市第二中学高一12月联考数学试题(解析版),共13页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年广西南宁市高一上学期12月联考数学试题(Word版含答案),共10页。试卷主要包含了有一组实验数据如表等内容,欢迎下载使用。












