湖北省十堰东风国际学校2020-2021学年高一下学期期末数学模拟卷1+Word版含答案

这是一份湖北省十堰东风国际学校2020-2021学年高一下学期期末数学模拟卷1+Word版含答案，共9页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
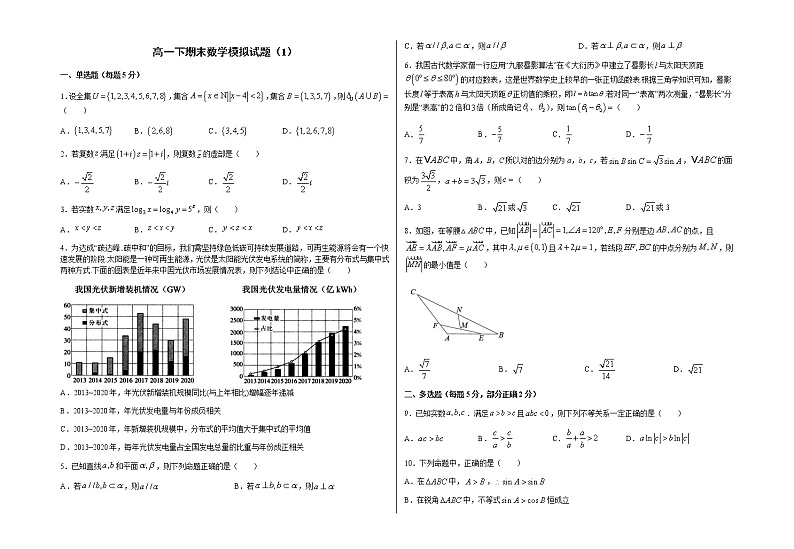
高一下期末数学模拟试题（1）一、单选题（每题5分）1．设全集，集合，集合，则（    ）A． B． C． D．2．若复数满足，则复数的虚部是（    ）A． B． C． D．3．若实数满足，则（    ）A． B． C． D．4．为达成“碳达峰､碳中和”的目标，我们需坚持绿色低碳可持续发展道路，可再生能源将会有一个快速发展的阶段.太阳能是一种可再生能源，光伏是太阳能光伏发电系统的简称，主要有分布式与集中式两种方式.下面的图表是近年来中国光伏市场发展情况表，则下列结论中正确的是（    ）
A．2013~2020年，年光伏新增装机规模同比(与上年相比)增幅逐年递减B．2013~2020年，年光伏发电量与年份成负相关C．2013~2020年，年新增装机规模中，分布式的平均值大于集中式的平均值D．2013~2020年，每年光伏发电量占全国发电总量的比重与年份成正相关5．已知直线和平面，则下列命题正确的是（    ）A．若，则                    B．若，则C．若，则                   D．若，则6．我国古代数学家僧一行应用“九服晷影算法”在《大衍历》中建立了晷影长与太阳天顶距的对应数表，这是世界数学史上较早的一张正切函数表.根据三角学知识可知，晷影长度等于表高与太阳天顶距正切值的乘积，即.若对同一“表高”两次测量，“晷影长”分别是“表高”的倍和倍（所成角记、），则（    ）A． B． C． D．7．在中，角A，B，C所以对的边分别为a，b，c，若，的面积为，，则（    ）A．3 B．或 C． D．或38．如图，在等腰△中，已知分别是边的点，且，其中且，若线段的中点分别为，则的最小值是（    ）A．                  B．                C．              D．二、多选题（每题5分，部分正确2分）9．已知实数．满足且，则下列不等关系一定正确的是（    ）A． B． C． D．10．下列命题中，正确的是（    ）A．在中，，B．在锐角中，不等式恒成立C．在中，若，则必是等腰直角三角形D．在中，若，，则必是等边三角形11．将曲线，上每个点的横坐标伸长为原来的2倍（纵坐标不变），得到的图像，则下列说法正确的是（    ）A．B．在上的值域为C．的图像关于点对称D．的图像可由的图像向右平移等个单位长度得到12．如图，在正方体中，，分别是，的中点，为线段上的动点(不含端点)，则下列结论中正确的是（    ） A．平面B．存在点使得C．存在点使得异面直线与所成的角为60°D．三棱锥的体积为定值 三、填空题（每题5分）13．如图，已知用斜二测画法画出的的直观图是边长为的正三角形，原的面积为_________.                  14．如图，在梯形中，，，，点是的中点，则______.15．已知，若，则_________.16．任意一个多面体，例如正六面体，假定它的面是用橡胶薄膜做成的，如果充以气体那么它就会连续(不破裂)变形，最后可变为一个球面.像这样，表面连续变形，可变为球面的多面体称为简单多面体.多面体欧拉定理是指对于简单多面体，其各维对象数总满足一定的数量关系，在三维空间中，多面体欧拉定理可表示为：顶点数面数棱数.正多面体的每个面都是正边形，顶点数是，棱数为，面数是，每个顶点连的棱数是，则下面对于正多面体的描述正确的是___________.①在正十二面体中，满足等式：；②在正多面体中，满足等式：；③在三维空间中，正多面体有且仅有4种；④以正六面体各面中心为顶点作一个正八面体，正六面体与正八面体的体积之比为；⑤以正六面体各面中心为顶点作一个正八面体，正六面体与正八面体的表面积之比为.四、解答题（共70分，其中17题10分，18-22题每题12分）17．（1）已知平面向量、，其中，若，且，求向量的坐标表示；（2）已知平面向量、满足，，与的夹角为，且（+）（），求的值.18．某科研课题组通过一款手机APP软件，调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”)，得到如下的频数分布表：周跑量人数100120130180220150603010（1）补全该市1000名跑步爱好者周跑量的频率分布直方图；周跑量小于20公20公里到不小于40类别休闲跑者核心跑者精英跑者装备价格250040004500（2）根据以上图表数据，试求样本的中位数及众数(保留一位小数)；（3）根据跑步爱好者的周跑量，将跑步爱好者分成以下三类，不同类别的跑者购买的装备的价格不一样(如表)，根据以上数据，估计该市每位跑步爱好者购买装备，平均需要花费多少元？19．已知函数在一个周期内的图象如图所示.                       （1）求的解析式；（2）将函数的图象向右平移个单位长度后，得到函数的图象，求在上的单调递增区间.20．如图，为圆锥的顶点，是圆锥底面的圆心，是底面的内接正三角形，为上一点，∠APC=90°． （1）证明：平面PAB⊥平面PAC；（2）设DO=，圆锥的侧面积为，求三棱锥P−ABC的体积.21．在①，②，③这三个条件中任选一个，补充到下面问题中，并解答问题.在中，内角A，B，C的对边长分别为a，b，c，且           .（1）求角A的大小；（2）若是锐角三角形，且，求边长c的取值范围.（注：如果选择多个条件分别解答，则按第一个解答计分）22．设且，，已知函数.（1）当时，求不等式的解；（2）若函数在区间上有零点，求的取值范围.  期末模拟试卷（一）参考答案题号123456789101112答案BCBDCDDCBCABDBDABD13．     14．    15．            16．①⑤.1． ，则所以2． ，复数的虚部是，3． 解：设，则，设，，作出函数的图像，如图所示，由图可得，所以，4． A，2013~2020年，年光伏新增装机规模同比(与上年相比)增幅逐年递减，前几年递增，后面递减，故A错误；B，2013~2020年，年光伏发电量与年份成正相关，故B错误；C，由图表可以看出，每一年装机规模，集中式都比分布式大，因此分布式的平均值小于集中式的平均值，故C错误；D，根据图表可知，2013~2020年，每年光伏发电量占全国发电总量的比重随年份逐年增加，故每年光伏发电量占全国发电总量的比重与年份成正相关，故D正确.5．对于A选项，若，，则或，A选项错误；对于B选项，若，则或或与相交，B选项错误；对于C选项，若，则，C选项正确；对于D选项，若，则可能或，D选项错误.6． 由题意知，，所以.7． 由得，所以，，又，所以，，，时，，时，，8． 在等腰△中，，则，∵分别是边的点，∴，，而，∴两边平方得：，而，∴，又，即，∴当时，最小值为，即的最小值为.9． 由已知得或，所以，A项错误；，因为，，，所以，B项正确；由题意知，则，C项正确；当，，时，显然D项错误．10． 对于，由，可得：，利用正弦定理可得：，正确；对于，在锐角中，，，，，，因此不等式恒成立，正确；对于，在中，由，利用正弦定理可得：，，，，或，或，是等腰三角形或直角三角形，因此是假命题，错误.对于，由于，，由余弦定理可得：，可得，解得，可得，故正确.11．,所以,所以对于A选项, ,故A选项错误；对于B选项，当时，，所以，故B选项正确；对于C选项，的图像关于点对称，故C选项错误；对于D选项，的图像向右平移等个单位长度得到，故D选项正确.12． 如图，易证，平面，则有平面，故A正确；设中点为，若为中点，则有，，，则平面，则，因为，所以，故B正确；设正方体棱长为2，取中点为，连接，因为，所以异面直线与所成的角即为，在直角三角形中，，即，故C错误；易知点到平面的距离为定值，则三棱锥的体积为定值，故D正确.13． 由题得又，所以原的面积为【点睛】结论点睛：本题考查利用斜二测画法求原视图的面积，利用斜二测画法的原视图与直观图的面积比为：，考查学生的运算能力，属于基础题。14． 令，则，又，，∴△为等边三角形，，连接，易知△、△都是直角三角形且，∴综上，有，，，∴在△中，.15． ，有，又，则，，，，.16．①由欧拉定理：顶点数+面数-棱数=2得，所以①正确.不妨举反例，在正六面体(正方体)中，，，，，，则，，，所以②错误.在三维空间中，正多面体有且仅有5种分别为正四面体､正六面体､正八面体､正十二面体､正二十面体，如图所示，所以③错误.④⑤如图所示：不妨设正六面体(正方体)的棱长为2，正八面体可以看成为两个全等正四棱锥的组合体，则正四棱锥的高为1，棱长为，所以正六面体的体积为，正八面体的体积为，所以正六面体与正八面体的体积之比为.正方体的表面积为，正八面体的表面积为，所以正六面体与正八面体的表面积之比为，所以④错误，⑤正确.故答案为：①⑤.17． （1）设，由，可得，由题意可得，解得或.因此，或；（2），化简得，即，解得18． （1）补全该市1000名跑步爱好者周跑量的频率分布直方图，如下：（2）中位数的估计值：由，，所以中位数位于区间中，设中位数为，则，解得.即样本中位数是29.2.    因为样本中频率最高的一组为[30,35),所以样本的众数为32.5.（3）依题意可知，休闲跑者共有人，核心跑者人，精英跑者人，所以该市每位跑步爱好者购买装备，平均需要元.即该市每位跑步爱好者购买装备，平均需要3720元.  19．【详解】（1）由图可得函数的最小正周期为，所以，， ，则，，则，，则，所以，，因为，所以，，所以，；（2）由题意可得，令，，得，，记，则.因此，函数在上的增区间是、.20． （1）连接，为圆锥顶点，为底面圆心，平面，在上，，是圆内接正三角形，，≌，，即，平面平面，平面平面；（2）设圆锥的母线为，底面半径为，圆锥的侧面积为，，解得，，在等腰直角三角形中，，在中，，三棱锥的体积为.  21．解：（1）选条件①.因为，所以，根据正弦定理得，，    由余弦定理得，，因为A是的内角，       所以选条件②，因为，由余弦定理，整理得，由余弦定理得，，    因为A是的内角，    所以.选条件③，因为，.，即因为，.         （2）因为，为锐角三角形，所以，解得在中，，所以，即.由可得，， 所以，所以.22．解：（1），不等式可化为若，则，解得，所以不等式的解集为.若，则，解得，所以不等式的解集为.综上所述：，的解集为；，的解集为.（2）.令，即，∵，∴，∴；∴ .设，则，∴或，解得或.