安徽省合肥市第八中学2020-2021学年高一下学期超越班数学限时作业（8）+Word版含解析

合肥八中高一（下）超越班数学单元练习（8）

一、单选题

1．下列命题正确的是（    ）

①平行于同一条直线的两条直线平行；②平行于同一条直线的两个平面平行；

③平行于同一个平面的两条直线平行；④平行于同一个平面的两个平面平行

A．①② B．③④ C．①④ D．②③

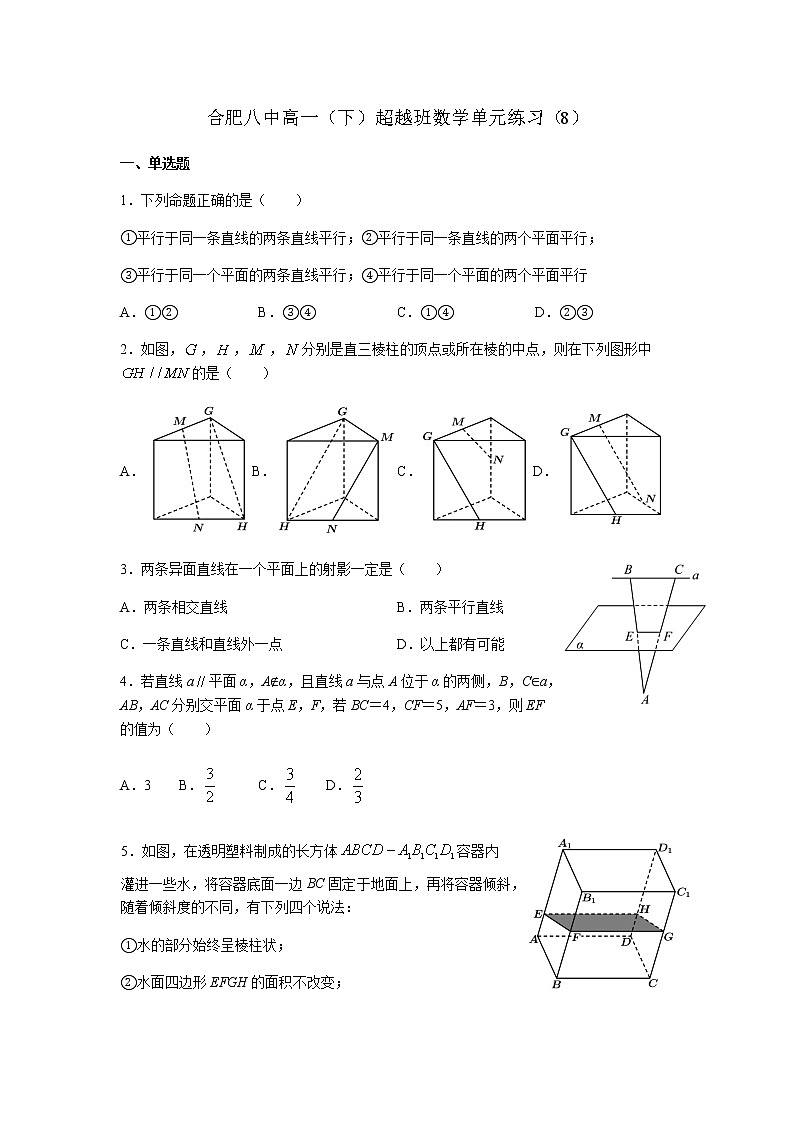
2．如图，，，，分别是直三棱柱的顶点或所在棱的中点，则在下列图形中的是（    ）

A．B．C．D．

3．两条异面直线在一个平面上的射影一定是（    ）

A．两条相交直线 B．两条平行直线

C．一条直线和直线外一点 D．以上都有可能

4．若直线a平面α，A∉α，且直线a与点A位于α的两侧，B，C∈a，AB，AC分别交平面α于点E，F，若BC＝4，CF＝5，AF＝3，则EF的值为（    ）

A．3    B． C．    D．

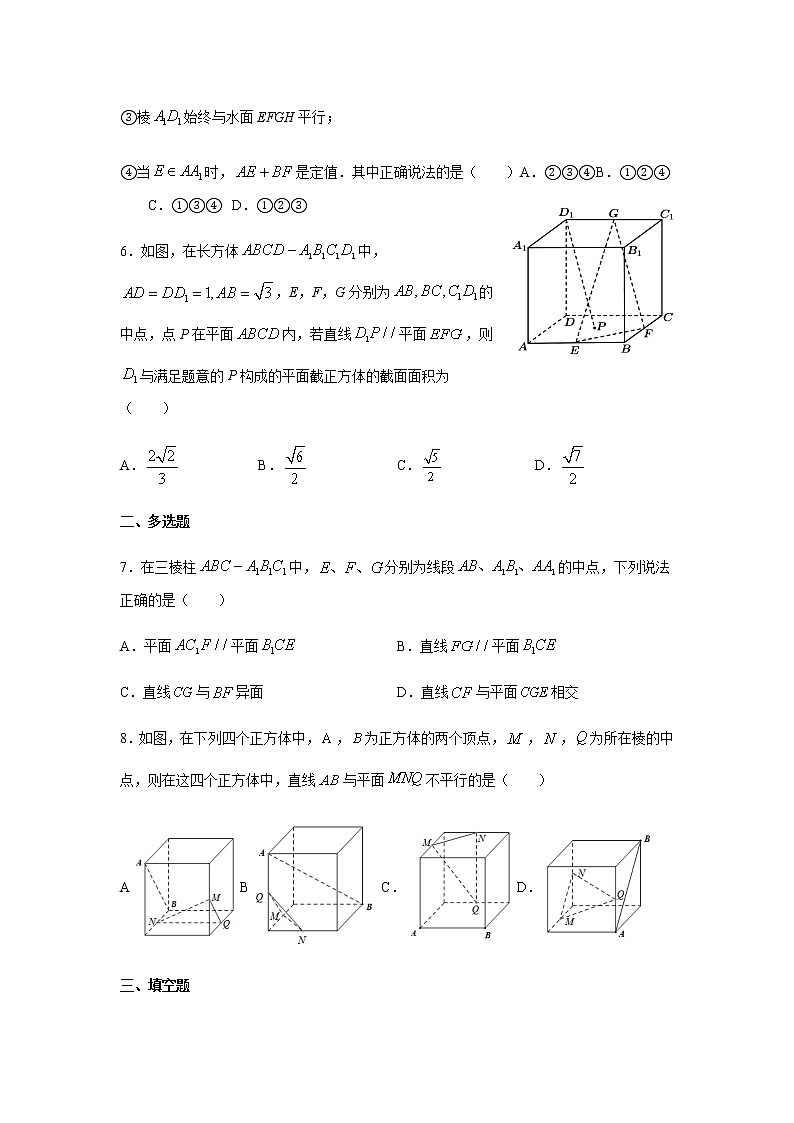
5．如图，在透明塑料制成的长方体容器内灌进一些水，将容器底面一边BC固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个说法：

①水的部分始终呈棱柱状；

②水面四边形EFGH的面积不改变；

③棱始终与水面EFGH平行；

④当时，是定值．其中正确说法的是（    ）A．②③④ B．①②④ C．①③④ D．①②③

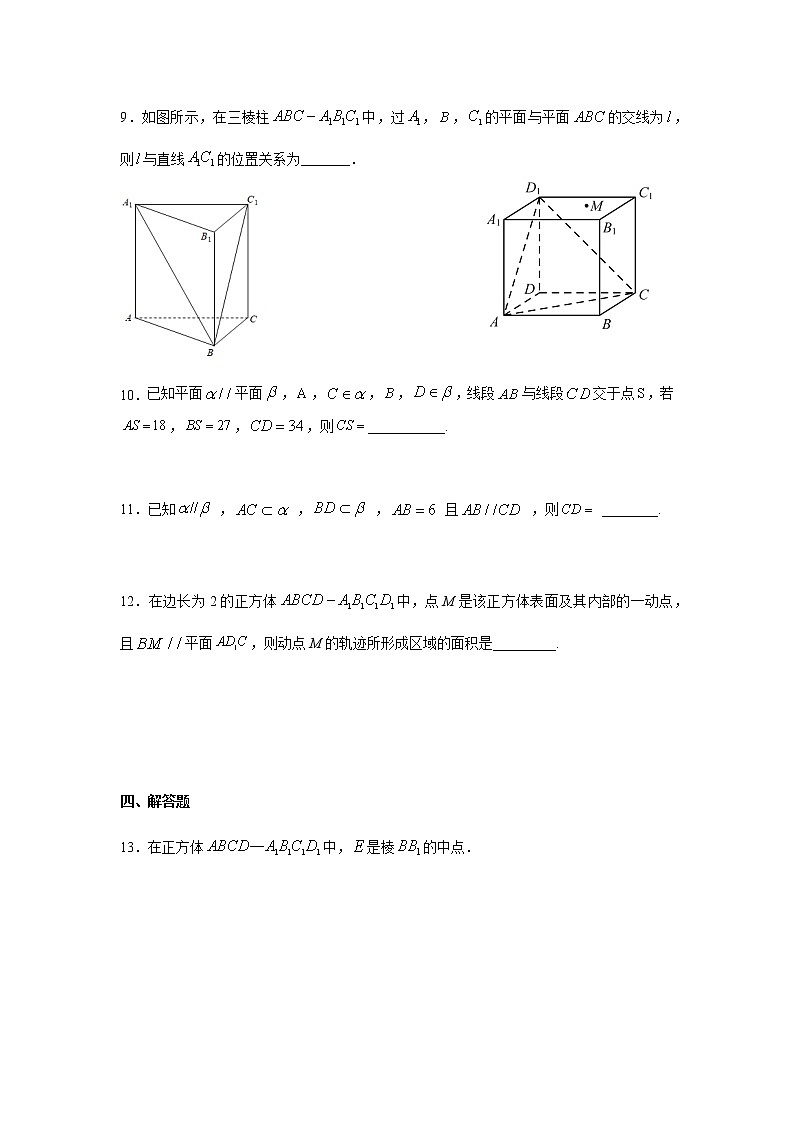
6．如图，在长方体中，，E，F，G分别为的中点，点P在平面内，若直线平面，则与满足题意的P构成的平面截正方体的截面面积为（    ）

A． B． C． D．

二、多选题

7．在三棱柱中，分别为线段的中点，下列说法正确的是（    ）

A．平面平面 B．直线平面

C．直线与异面 D．直线与平面相交

8．如图，在下列四个正方体中，，为正方体的两个顶点，，，为所在棱的中点，则在这四个正方体中，直线与平面不平行的是（    ）

ABC．D．

三、填空题

9．如图所示，在三棱柱中，过，，的平面与平面的交线为，则与直线的位置关系为_______．

10．已知平面平面，，，，，线段与线段交于点，若，，，则___________.

11．已知 ， ， ， 且 ，则 ________.

12．在边长为2的正方体中，点M是该正方体表面及其内部的一动点，且平面，则动点M的轨迹所形成区域的面积是_________.

四、解答题

13．在正方体中，是棱的中点．

（1）求证：平面．   

（2）若是棱的中点，求证：平面平面．

14．如图，正方体，棱长为4，分别为上的点，点为中点，且．

（1）当时，求证：平面；

（2）当为何值时，三棱锥的体积最大？，并求出最大值是多少

合肥八中高一（下）超越班数学单元练习（8）

一、单选题

1．下列命题正确的是（    ）

①平行于同一条直线的两条直线平行；

②平行于同一条直线的两个平面平行；

③平行于同一个平面的两条直线平行；

④平行于同一个平面的两个平面平行

A．①② B．③④ C．①④ D．②③

【答案】C

【分析】

根据空间平行关系分别判断每个命题即可.

【详解】

①由平行线间的传递性可知，平行于同一条直线的两条直线平行，故①正确；

②平行于同一条直线的两个平面平行或相交，故②错误；

③平行于同一个平面的两条直线平行、相交或异面，故③错误；

④根据平面平行的性质，平行于同一个平面的两个平面平行，故④正确.

故选：C.

2．如图，，，，分别是直三棱柱的顶点或所在棱的中点，则在下列图形中的是（    ）

A． B．

C． D．

【答案】D

【分析】

根据异面直线的定义、平行线的性质、平行四边形的性质进行判断即可.

【详解】

解：对于A，若，可得，，，四点共面，则直线，共面，

这与，异面矛盾，所以A中的两直线不平行；

由异面直线的定义可得B，C中的两直线，为异面直线；

由，为中点，可得，且，则四边形为平行四边形，

D中的两直线为平行直线.

故选：D.

3．两条异面直线在一个平面上的射影一定是（    ）

A．两条相交直线 B．两条平行直线

C．一条直线和直线外一点 D．以上都有可能

【答案】D

【分析】

根据投影面与两条异面直线的关系判断投影的情形．

【详解】

如果所给的平面与两条异面直线中的一条垂直，则两条异面直线在一个平面上的射影为一条直线和直线外一点；

若所给的平面与两条件异面直线均不垂直，但与异面直线的公垂线平行，则两条异面直线在一个平面上的射影为两条平行直线；

若所给的平面与两条件异面直线均不垂直，且与异面直线的公垂线不平行，则两条异面直线在一个平面上的射影为两条相交直线；

故选：D．

4．若直线a平面α，A∉α，且直线a与点A位于α的两侧，B，C∈a，AB，AC分别交平面α于点E，F，若BC＝4，CF＝5，AF＝3，则EF的值为（    ）

A．3 B． C． D．

【答案】B

【分析】

由线面平行的性质得出线段间的比例，可得选项．

【详解】

解：∵BC∥α，且平面ABC∩α＝EF，

∴EF∥BC，∴＝，即＝．

∴EF＝．

故选：B．

5．如图，在透明塑料制成的长方体容器内灌进一些水，将容器底面一边BC固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个说法：

①水的部分始终呈棱柱状；

②水面四边形EFGH的面积不改变；

③棱始终与水面EFGH平行；

④当时，是定值．其中正确说法的是（    ）

A．②③④ B．①②④ C．①③④ D．①②③

【答案】C

【分析】

①由平面平行平面判断；②由四边形为矩形，变化而不变判断；③由始终与EH平行判断；④由水的体积是定值，高不变，底面面积不变判断.

【详解】

①由棱柱的特征知：平面平行平面，故正确；

②因为四边形是矩形，的长度变化，长度不变，所以面积是改变的，故错误；

③因为，平面EFGH，平面EFGH，所以平面EFGH，故正确；

④因为水的体积是定值，高不变，所以底面面积不变，所以时，是定值．故正确．

故选：C．

6．如图，在长方体中，，E，F，G分别为的中点，点P在平面内，若直线平面，则与满足题意的P构成的平面截正方体的截面面积为（    ）

A． B． C． D．

【答案】D

【分析】

根据线面平行的判定定理、面面平行的判定定理进行求解即可.

【详解】

如图，连接，

因为E，F，G分别为的中点，

所以平面，则平面，

因为，所以同理得平面，

又，得平面平面，

所以点P在直线上，则与满足题意的P构成的平面截正方体的截面为，

在中，有，所以．

故选：D

二、多选题

7．在三棱柱中，分别为线段的中点，下列说法正确的是（    ）

A．平面平面 B．直线平面

C．直线与异面 D．直线与平面相交

【答案】AC

【分析】

在三棱柱中，得到，结合面面平行的判定，可判定A是正确的；由，得到与相交，可判定B错误；由，得到平面，进而可判定C正确；由线面平行的判定定理，可得判定D错误.

【详解】

对于A中，在三棱柱中，分别为线段的中点，

所以，

因为，所以平面平面，所以A是正确的；

对于B中，因为分别是线段的中点，

所以，所以与相交，

所以直线与平面相交，所以B错误；

对于C中，因为分别为线段的中点，所以，

因为平面平面，所以平面，

因为，所以与是异面直线，所以C正确；

对于D中，因为,平面，平面，

所以直线平面，所以D错误.

故选：AC.

【点睛】

解答空间中点、线、面位置关系的判定问题常见解题策略：

1、对空间平行关系的转化条件理解不透导致错误；对面面平行判定定理的条件“面内两相交直线”认识不清导致错解；

2、对于空间中的垂直关系中确定线面垂直是关键，证明线线垂直则需借助线面垂直的性质，垂直关系的判定定理和性质定理合理转化是证明垂直关系的基本思想.

8．如图，在下列四个正方体中，，为正方体的两个顶点，，，为所在棱的中点，则在这四个正方体中，直线与平面不平行的是（    ）

A． B．

C． D．

【答案】BC

【分析】

根据线面平行的判定定理判断．

【详解】

A中如下图，由中位线定理，而，从而，平面，有线面平行；

B中，如下图，，在平面上，与显然相交，因此与平面相交，不平行．

C中，如下图，是所在棱中点，则，即平面，而在底面上，直线与直线相交，与平面相交，不平行．

D中，如下图，由中位线定理，而，从而，平面，有线面平行；

故选：BC．

【点睛】

关键点点睛：本题考查线面平行的判断，关键是找到线线平行．正方体中平行线很多，易于寻找，在说明线面相交时，注意线线相交一定要在一个平面内的两条直线才能确定是否相交．

三、填空题

9．如图所示，在三棱柱中，过，，的平面与平面的交线为，则与直线的位置关系为__．

【答案】平行

【分析】

利用线面平行的判定定理和线面平行的性质定理，即可判断出与直线平行．

【详解】

在三棱柱中，，平面，平面，

所以平面,又因为平面，且平面平面，

所以．

故答案为：平行

10．已知平面平面，，，，，线段与线段交于点，若，，，则___________.

【答案】或68

【分析】

由与相交，则与共面，则其所在面和平面、的交线平行，根据所给数据结合相似比，分点位于平面与平面之间和点位于平面与平面外进行讨论，即可得解.

【详解】

①如图，若点位于平面与平面之间，根据平面平行的性质定理，得，，

，

即，.

②如图，若点位于平面与平面外，根据平面平行的性质，得，

故答案为：或68.

11．已知 ， ， ， 且 ，则 ________.

【答案】6

【分析】

根据面面平行的性质可得解.

【详解】

如图，∵，

∴ 四点共面，

∵，且平面，平面，

∴，又，

∴四边形为平行四边形，

∴.

故答案为:6.

12．在边长为2的正方体中，点M是该正方体表面及其内部的一动点，且平面，则动点M的轨迹所形成区域的面积是_________.

【答案】

【分析】

由题意，求出作出过的平面与平面平行，该平面即为动点M的轨迹所形成区域，求出该区域的面积即可.

【详解】

如图，边长为2的正方体中，

动点M满足平面，

由面面平行的性质可得

当始终在一个与平面平行的面内，即满足题意，

过作与平面平行的平面，

连接，，，平面平面，

所以.

故答案为：

四、解答题

13．在正方体中，是棱的中点．

（1）求证：平面．   

（2）若是棱的中点，求证：平面平面．

【答案】（1）证明见解析；（2）证明见解析.

【分析】

（1）连，使，连，可得，即可证明；

（2）通过证明平面，再结合（1）即可证明.

【详解】

（1）连，使，连．

∵是正方形，，．

又是中点，，

，

又平面，平面，

∴平面．   

（2）∵是棱的中点，是棱的中点．

且，

是平行四边形，

，又平面，平面，

平面，

由（1）平面，又 ，

∴平面//平面．

14．如图，正方体，棱长为4，分别为上的点，点为中点，且．

（1）当时，求证：平面；

（2）当为何值时，三棱锥的体积最大？，并求出最大值是多少．

【答案】（1）证明见解析；（2）时，体积最大，且最大值为．

【分析】

（1）连结，可得，利用线面平行的判定定理可得平面，平面，从而证得面面平行，再由面面平行的性质定理即可证明.

（2），则，从而可得，利用基本不等式求出最大值即可求解.

【详解】

解：（1）当时，分别为中点，连结，

可得，

又因为平面，平面，

所以平面，

同理平面

又因为平面，平面，

所以平面平面，

又因为平面，所以平面．

（2）∵，则，

∴，

当且仅且，即时取等号．

∴最大值为2，∵平面，

∴．

．