数学九年级上册22.2 相似三角形的判定教学课件ppt

这是一份数学九年级上册22.2 相似三角形的判定教学课件ppt，共18页。PPT课件主要包含了判定相似方法二，相似三角形判定方法三，相似三角形判定方法四，一“排”，二“算”，三“判”等内容，欢迎下载使用。
相似三角形的性质：相似三角形的对应角相等，对应边成比例.
我们把三个角对应相等，且三条边对应成比例的两个三角形叫作相似三角形．
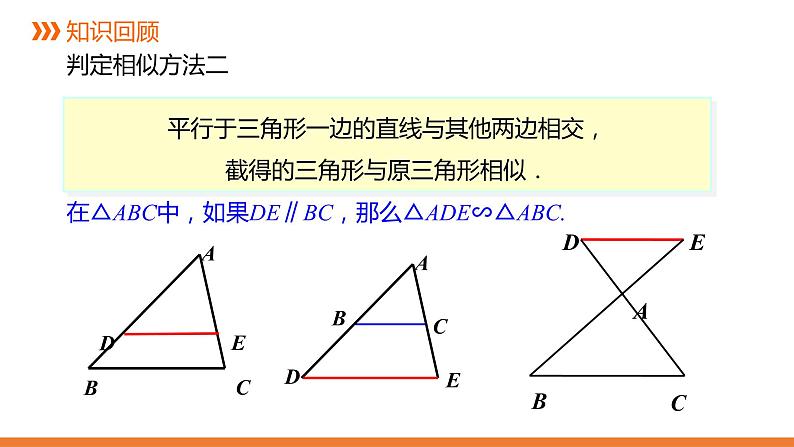
平行于三角形一边的直线与其他两边相交，截得的三角形与原三角形相似．
在△ABC中，如果DE∥BC，那么△ADE∽△ABC.
判定定理1 如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似.
∵ ∠A=∠A'， ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
即：两角分别相等的两个三角形相似 .
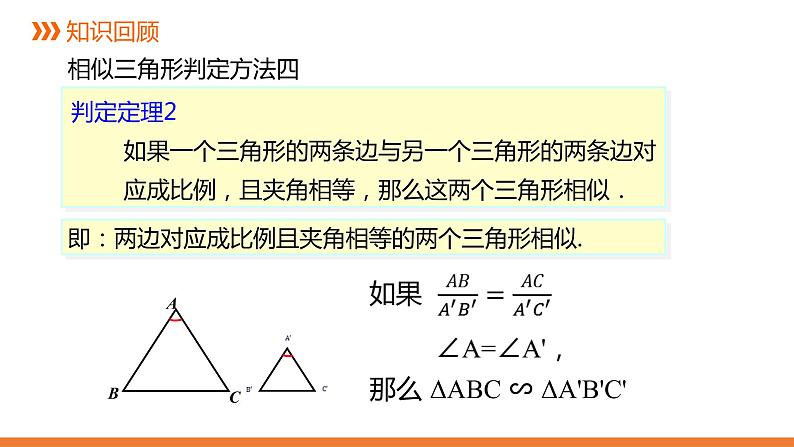
判定定理2 如果一个三角形的两条边与另一个三角形的两条边对应成比例，且夹角相等，那么这两个三角形相似．
即：两边对应成比例且夹角相等的两个三角形相似.
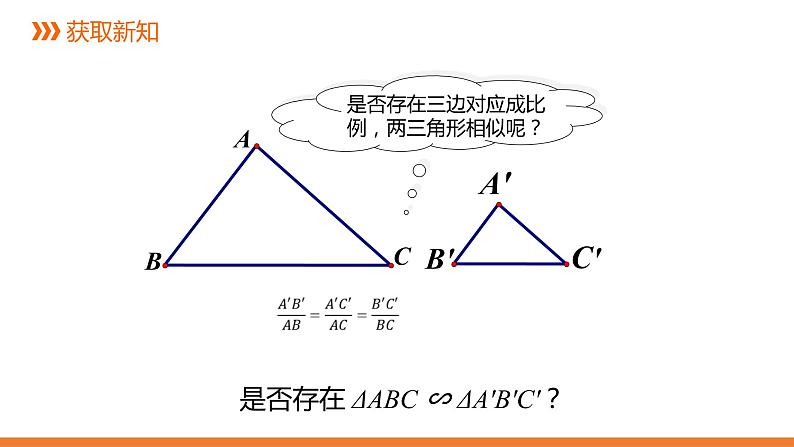
是否存在三边对应成比例，两三角形相似呢？
是否存在 ΔABC ∽ ΔA'B'C'？
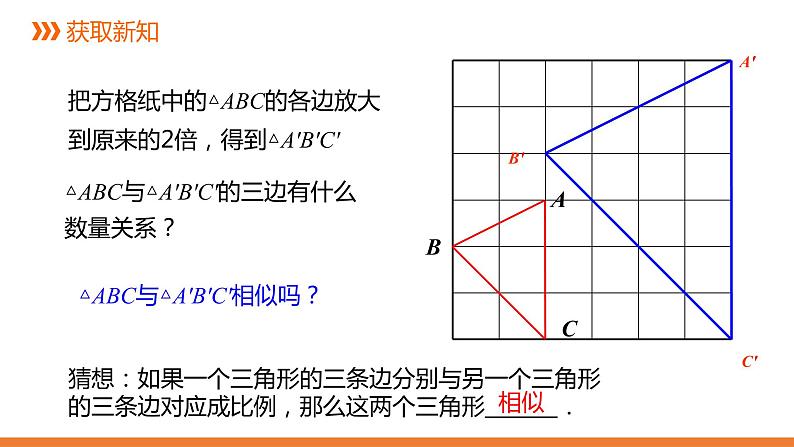
猜想：如果一个三角形的三条边分别与另一个三角形的三条边对应成比例，那么这两个三角形_______．
把方格纸中的△ABC的各边放大到原来的2倍，得到△A'B'C'
△ABC与△A'B'C'相似吗？
△ABC与△A'B'C'的三边有什么数量关系？
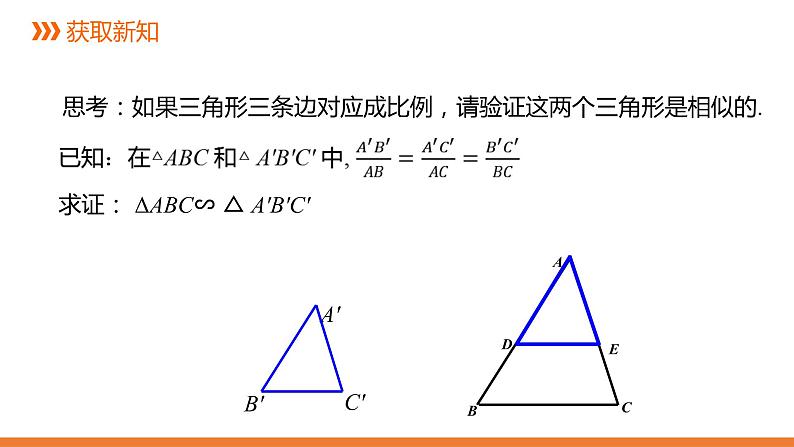
思考：如果三角形三条边对应成比例，请验证这两个三角形是相似的.
求证： ΔABC∽ △ A'B'C'
证明：在△ABC的边AB(或延长线)上截取AD=A′B′,
过点D作DE∥BC交AC于点E.
∴ △ADE∽△ABC，
判定定理3 如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．
即：三边成比例的两个三角形相似.
已知△ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12， BC=15， AC＝24 DE＝16， EF＝20， DF＝30
(2) AB=4， BC=8， AC＝10 DE＝20， EF＝16， DF＝8
(1) AB=3， BC=4， AC＝6 DE＝6， EF＝8， DF＝9
（大对大，小对小，中对中）
将每个三角形的三边的长度按大小顺序排列
利用三边判断两个三角形是否相似的步骤
计算最长边与最长边的比,较长边与较长边的比,最短边与最短边的比
由比值是否相等判断两个三角形是否相似
【1】两个直角三角形一定相似吗？ 两个等腰直角三角形呢？为什么？
1.所有的直角三角形不都相似；2.所有的等腰直角三角形都相似.
【2】两个等腰三角形一定相似吗？ 两个等边三角形呢？为什么？
1.所有的等腰三角形不都相似；2.所有的等边三角形都相似.
如图,在△ABC和△ADE，ABAD=BCDE=ACAE，∠BAD=20°,求∠CAE的度数.