青岛版九年级上册2.5 解直角三角形的应用授课ppt课件

这是一份青岛版九年级上册2.5 解直角三角形的应用授课ppt课件，共28页。PPT课件主要包含了∠A＋∠B＝90°，复习提问，新课引入，讲授新课，中考试题等内容，欢迎下载使用。
2.两锐角之间的关系呢?
3.边角之间的关系呢？
1.三边之间的关系是什么？
在解直角三角形的过程中，一般要用到的一些关系：
某探险者某天到达如图所示的点A 处时，他准备估算出离他的目的地——海拔为3 500 m 的山峰顶点B处的水平距离. 他能想出一个可行的办法吗？ 通过这节课的学习，相信你也行.
在进行测量时，从下向上看，视线与水平线的夹角叫做仰角；从上往下看，视线与水平线的夹角叫做俯角.
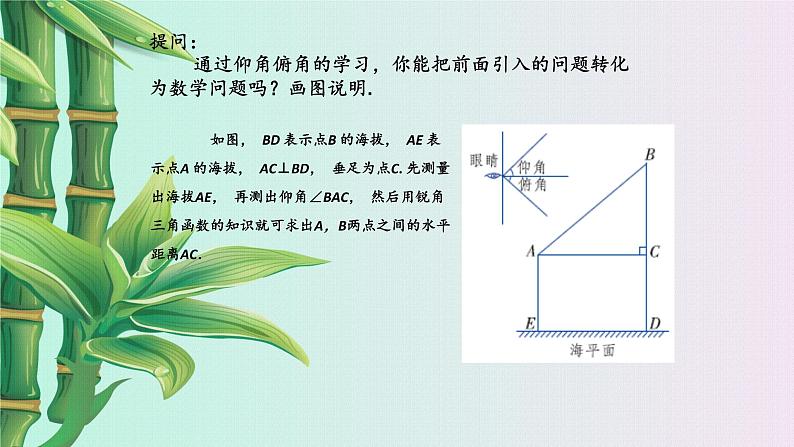
如图， BD 表示点B 的海拔， AE 表示点A 的海拔， AC⊥BD， 垂足为点C. 先测量出海拔AE， 再测出仰角∠BAC， 然后用锐角三角函数的知识就可求出A，B两点之间的水平距离AC．
提问： 通过仰角俯角的学习，你能把前面引入的问题转化为数学问题吗？画图说明.
∵ BD = 3500 m， AE = 1600 m， AC⊥BD，∠BAC = 40°，
因此， Ａ，B两点之间的水平距离AC约为2264 m.
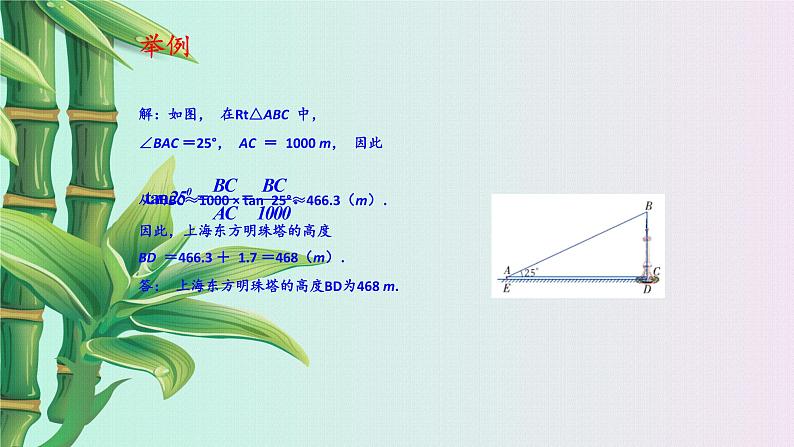
例1 如图，在离上海东方明珠塔底部1 000 m 的A 处， 用仪器测得塔顶的仰角∠BAC 为25°， 仪器距地面高AE 为1.7 m．求上海东方明珠塔的高度BD（结果精确到1 m）.
分析：在直角三角形中，已知一角和它的邻边，求对边利用该角的正切即可.
如图，一艘游船在离开码头A后，以和河岸成 30°角的方向行驶了500m到达B处，求B处与河岸的距离.
答：B处与河岸的距离约为250m．
在Rt△ABC中，∠C=90°，∠A=30°，AB=500m.
2.本节学习以后，能说说解直角三角形常见的两种基本图形吗？
1.什么是仰角？什么是俯角？
1.如图，在高出海平面100米的悬崖顶A处，观测海平面上一艘小船B，并测得它的俯角为45°，则船与观测者之间的水平距离BC＝ 米．
2.如图，小红同学用仪器测量一棵大树AB的高度，在C处测得∠ADG30，在E处测得∠AFG60，CE8米，仪器高度CD1.5米，求这棵树AB的高度（结果保留两位有效数字,
解：大树AB的高约为8.4米．
3.为促进我市经济的快速发展，加快道路建设，某高速公路建设工程中需修隧道AB，如图，在山外一点C测得BC距离为200m，∠CAB=54°，∠CBA=30°，求隧道AB的长．（参考数据：sin54°≈0.81，cs54°≈0.59，tan54°≈1.38， ≈1.73，精确到个位）
解：过点C作CD⊥AB于D，∵BC=200m，∠CBA=30°，∴在Rt△BCD中，CD= BC=100m， BD=BC•cs30°≈173（m），在Rt△ACD中，AD≈74（m），∴AB=AD+BD=173+74=247（m）．答：隧道AB的长为247m．
如图， 从山脚到山顶有两条路AB与BD， 问哪条路比较陡？ 右边的路BD陡些．如何用数量来刻画哪条路陡呢？
在图中，∠BAC 叫作坡角．坡角：坡面与地平面的夹角α叫坡角．
（坡度通常写成1 ∶ m的形式）．
例2 如图，一山坡的坡度为i = 1∶2 . 小刚从山脚A 出发， 沿山坡向上走了240 m 到达点C. 这座山坡的坡角是多少度？ 小刚上升了多少米？ （角度精确到0.01°，长度精确到0.1 m）
分析：在直角三角形ABC中，已知了坡度即角α的正切可求出坡角α，然后用α的正弦求出对边BC的长.
如图，拦水坝的横断面为梯形ABCD，根据图中数据求坡角a和β;
解：在Rt△AFB中，∠AFB=90°
在Rt△CDE中，∠CED=90°
例3 如图， 一艘船以40 km/h 的速度向正东航行， 在A 处测得灯塔C 在北偏东60°方向上， 继续航行1 h到达B 处，这时测得灯塔C 在北偏东30°方向上. 已知在灯塔C的四周30 km内有暗礁．问这艘船继续向东航行是否安全？
分析：在两个直角三角形中，分别利用30°、 60°角的正切，用同一个参量x表示出AD 、 BD的长，进而用方程思想求解.
因此，该船能继续安全地向东航行．
3.说说利用解直角三角形的知识解决实际问题 的一般过程是什么？
1.什么是坡比？2.东北方向指北偏东多少度？
（1）将实际问题抽象为数学问题（画出平面图形，转化为解直角三角形的问题）；（2）根据条件的特点，适当选用锐角三角形函数等去解直角三角形；（3）得到数学问题的答案,从而得到实际问题的答案.
1.如图，某水库堤坝横断面迎水坡AB的坡比是1： ，堤坝高BC=50m，则迎水坡面AB的长度是（ ）
2.周末，小亮一家在东昌湖游玩，妈妈在湖心岛P处观看小亮与爸爸在湖中划船（如图），小船从P处出发，沿北偏东60°方向划行200米到A处，接着向正南方向划行一段时间到B处.在B处小亮观测妈妈所在的P处在北偏西37°的方向上，这时小亮与妈妈相距多少米（精确到1米）？
解：过点P作PC⊥AB于C.在Rt△APC中，AP=200m，∠ACP=90°，∠PAC=60°.∴ PC= 200×sin60°=200 × =100 m.∵在Rt△PBC中，sin37°= ， ∴PB ≈ 289（m）答：小亮与妈妈相距约289米.