

2019年浙江宁波江北区初三一模数学试卷(详解版) (1)
展开
这是一份2019年浙江宁波江北区初三一模数学试卷(详解版) (1),共23页。试卷主要包含了在下列实数中,无理数是.,下列计算正确的是.,一元二次方程的解为.等内容,欢迎下载使用。
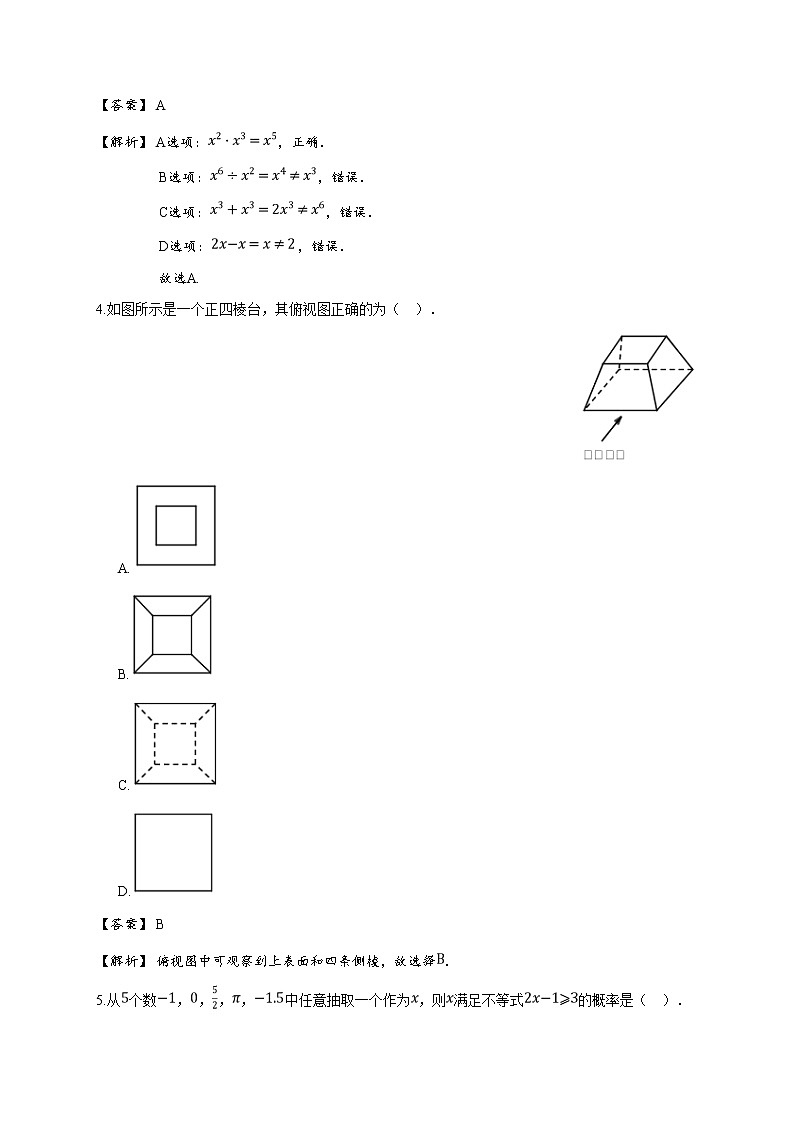
2019年浙江宁波江北区初三一模数学试卷选择题(每小题4分,共48分)1.在下列实数中,无理数是( ).A.B.C.D.【答案】 B【解析】 方法一:是无理数,故选:.方法二:、、均为有理数,为无理数,∴选.2.截止年月日,中国科幻电影《流浪地球》的票房约为亿元,成为中国科幻电影的里程碑.其中亿用科学记数法表示为( ).A.B.C.D.【答案】 C【解析】 亿.故选.3.下列计算正确的是( ).A.B.C.D.【答案】 A【解析】 A选项:,正确.B选项:,错误.C选项:,错误.D选项:,错误.故选A.4.如图所示是一个正四棱台,其俯视图正确的为( ).A.B.C.D.【答案】 B【解析】 俯视图中可观察到上表面和四条侧棱,故选择.5.从个数,,,,中任意抽取一个作为,则满足不等式的概率是( ).A.B.C.D.【答案】 B【解析】 ∵的解是,∴仅与符合题意,∴.故选.6.将一副三角板如图放置,其中,,,其中点落在线段上,且,则的度数为( ).A.B.C.D.【答案】 D【解析】 ∵,,∴,∵,∴,∵,,∴,∴.故选.7.一元二次方程的解为( ).A.,B.,C.,D.,【答案】 D【解析】 ∵,∴,∴,.故选.8.如图,是⊙的内接三角形,,,则⊙的直径长为( ).A.B.C.D.【答案】 C【解析】 连接,,∵,又∵,∴正,∴,∴直径为.故选.9.一组数,,,,,,是“斐波那契数列”的一部分,若去掉其中的两个数后,这组数的中位数、众数保持不变,则去掉的两个数可能是( ).A.,B.,C.,D.,【答案】 A【解析】 原数据中位数是,众数是,∵众数不变,∴不可能去掉,又∵中位数不变,∴一定删去和一个大于的数据,∴选择.10.如图,在边长为的正方形中,点是边上的一点,连接,将绕着点顺时针旋转一定的角度,使得点落在线段上,记为点,此时点恰好落在边上,记为点,则的长为( ).A.B.C.D.【答案】 D【解析】 由旋转可知≌,∴,,∵和中,,∴≌,∴,∴,∴.11.下列尺规作图中,能确定圆心的是( ).①如图,在圆上任取三个点,,,分别作弦,的垂直平分线,交点即为圆心;②如图,在圆上任取一点,以为圆心,小于直径长为半径画弧交圆于,两点,连接,,作的平分线交圆于点,作弦的垂直平分线交于点,点即为圆心;③如图,在圆上截取弦,连接,,,分别作与的平分线,交点即为圆心.A.①②B.①③C.②③D.①②③【答案】 A【解析】 ①三角形的中垂线交点即外接圆圆心(外心),∴①能确定圆心;②由垂经定理可知是的直径,∴中点是圆心,∴②能确定圆心;③当时,能确定圆心,仅有,则条件不充分.∴①②正确.故选.12.已知点,在抛物线的图象上,且,则线段长的最大值、最小值分别是( ).A.,B.,C.,D.,【答案】 C【解析】 ,,∴,∴,,∴,.故选.填空题(每小题4分,共24分)1.因式分解: .【答案】 【解析】 .2.一个圆锥的底面半径长为,母线长为,则这个圆锥的侧面积为 .【答案】 【解析】 ().3.等腰直角在平面直角坐标系中如图所示,点为坐标原点,直角顶点的坐标为,点在反比例函数的图象上,则的值为 .【答案】 【解析】 过点作轴垂线于点,作交于点,由三垂直模型易知,≌,∴,,∴,∴.故答案为:.4.如图,在中,点,,分别在边,,上,,,,的面积为,则四边形的面积为 .【答案】 【解析】 ∵且,∴,∴,又∵,∴,∴.故答案为:.5.如图,在的正方形网格图中,以格点为圆心各画四条圆弧,则这四条圆弧所围成的阴影部分面积为 .【答案】 【解析】如图对空白部分进行划分,,,,,∴.6.如图,在菱形中,,,点在上运动(不与,重合),将四边形沿直线翻折后,点落在处,点落在处,与交于点,当时,长为 .【答案】 【解析】 延长交于,作交于点,由对称可知,,,∴,,∴,∵,∴,∴,设,在中,,∴,在中,,,∴,∴,∴.解答题(本大题有8小题,共78分)1.先化简,再求值:,其中.【答案】 .【解析】 原式,.当时,原式.2.“数学来源于生活,又运用于生活”.曹老师为了了解所教班级学生利用数学知识解决实际问题的能力,编制若干问题对全班学生进行了一次测试,并将测试结果分成四类,:特别强;:强;:一般;:较弱.以下是由调查测试结果绘制的两幅不完整的统计图,请你根据统计图完成以下解答.( 1 )曹老师的班级共有 名学生.( 2 )将下面条形统计图的类部分补充完整.( 3 )扇形统计图中,类对应的圆心角为多少度.【答案】 (1) (2) 画图见解析.(3) .【解析】 (1) 根据题意得:(名).(2) 类的人数为:(名),则类的女生有(名),补全图形为:(3) 方法一:类占总数的百分比为,∴类对应的圆心角为:.方法二:.故答案为:类对应的圆心角为度.3.如图,是正方形网格图中的格点三角形(顶点在格点上),请分别在图,图的正方形网格内按下列要求画一个格点三角形.( 1 )在图中,以为边画直角三角形(与不重合),使它与全等.( 2 )在图中,以为边画直角三角形,使它的一个锐角等于,且与不全等.【答案】 (1) 画图见解析.(2) 画图见解析.【解析】 (1) 如下图:即为所求.(2) 如下图:即为所求(画出一个即可).4.如图,二次函数图象的顶点为,且与反比例函数的图象交于点.( 1 )求二次函数与反比例函数的解析式.( 2 )判断原点是否在二次函数的图象上,并说明理由.( 3 )根据图象直接写出二次函数的值小于反比例函数的值时,自变量的取值范围.【答案】 (1) 二次函数表达式为:.反比例函数表达式为:.(2) 原点在二次函数图象上.证明见解析.(3) 或.【解析】 (1) 由题意得:设二次函数表达式为:,把代入得:,,∴二次函数表达式为:.设反比例函数表达式为:,把代入得:,∴.(2) 把代入,,∴原点在二次函数图象上.(3) 或.5.为了增强体质,小明计划晚间骑自行车训练,他在自行车上安装了夜行灯.如图,夜行灯射出的光线、与地面的夹角分别为和,该夜行灯照亮地面的宽度长为米,求该夜行灯距离地面的高度的长.(参考数据:,,,).【答案】 该夜行灯距离地面高度为米.【解析】 设高度,在中,,在中,,∵,∴,∴,即该夜行灯距离地面高度为米.故答案为:该夜行灯距离地面高度为米.6.“宁波国际山地马拉松赛”于年月日在江北区举行.小林参加了环绕荪湖的迷你马拉松项目(如图),上午起跑,赛道上距离起点处会设置饮水补给站.在比赛中,小林匀速前行,他距离终点的路程与跑步的时间的函数图象的一部分如图所示. ( 1 )求小林从起点跑向饮水补给站的过程中与的函数表达式.( 2 )求小林跑步的速度,以及图中的值.( 3 )当跑到饮水补给站时,小林觉得自己跑得太悠闲了,他想挑战自己在上午之前跑到终点,那么接下来一段路程他的速度至少应为多少?【答案】 (1) .(2) 小林的速度为,.(3) .【解析】 (1) 设,将和代入得:,解得,∴.∴小林从起点站跑到第一个饮料站的过程中与之间的函数表达式为:.(2) ∵,∴小林的速度为,将代入,得,∴.(3) 设接下来一段路程小林的速度为,则,解得.答:要使小林能在之前跑到终点,那么接下来一段路程他的速度至少应为每小时.7.平行四边形的对角线相交于点,的外接圆交于点,且圆心恰好落在边上,连接,若.( 1 )求证:为切线.( 2 )求的度数.( 3 )若,求的长.【答案】 (1) 证明见解析.(2) .(3) .【解析】 (1) 如图,连结,在平行四边形中,.∴.∵,∴.∴.∵,∴,∴,∴为圆切线.(2) 如图,连结,在平行四边形中,.∵,∴.∵,∴.在中,,∴.(3) ∵四边形内接于圆,∴,.∵,∴.∴,∴.过点作.∵,∴.∵,∴,∴,∴.8.等边与正方形如图放置,其中,两点分别在,上,且.( 1 )求的度数.( 2 )当正方形沿着射线方向以每秒个单位长度的速度平移时,的长度随着运动时间变化的函数图象如图所示,且当时,有最小值.① 求等边的边长.② 连接,在平移的过程中,求当与同时为等腰三角形时的值.③ 从平移运动开始,到恰落在边上时,请直接写出外接圆圆心的运动路径的长度.【答案】 (1) .(2) .(3) 当,时与同时为等腰三角形.(4) .【解析】 (1) ∵为等边三角形,∴,∵,∴.(2) 的运动路径为一条平行于的射线,∴当时,的长度最短,由函数图象得:此时正方形移动,即,,,∵,则,∴,∴,∴,即的边长为.(3) 如图,当点在上时,∵,∴若为等腰三角形,则一定,又∵,∴也为等腰三角形,则,如图,当点在延长线上时,∵,∴若为等腰三角形,则一定为等边三角形,∴,又,∴也为等腰三角形,则,综上所述:当,时与同时为等腰三角形.(4) 方法一:如图,当落在边上时,即点运动到了点,过点作,过点作,∵,∴,,∵,∴,∴,即点平移了个单位长度.如图,设为外接圆圆心,当正方形平移时,点沿着射线方向平移,,在射线上任取一定点,连结并将绕点逆时针旋转至,连结,∵,∴,∴为等边三角形,∴,,∴,∴≌,且当点平移时,始终成立,∴始终等于,且所在直线与所在直线夹角为,即点在射线上运动,∴点运动路径等于点的运动路径长,∴当落在边上时,点平移了个单位长度.∴点运动路径长为也为.方法二:如图,以为原点,所在直线为轴建立坐标系,当平移了个单位后,,,,∴与的中垂线分别:与直线,交点即为外接圆圆心,,∴点在直线上运动,当落在边上时,,此时,当时,,∴点运动路径长为.
相关试卷
这是一份[数学][期末]2023~2024学年浙江省宁波市江北区七年级(下)期末数学试卷(有详解),共12页。
这是一份2024年浙江省宁波市江北区中考一模考试数学试卷(含答案),共13页。
这是一份2024年浙江省宁波市江北区中考一模考试数学试卷,文件包含江北一模数学试卷_1714015881984pdf、江北一模数学答案_1714015918186pdf等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。








