初中数学苏科版九年级上册2.2 圆的对称性课文配套课件ppt

这是一份初中数学苏科版九年级上册2.2 圆的对称性课文配套课件ppt，共16页。PPT课件主要包含了问题情境，实践探索一，推理证明，展示交流，议一议，怎样说理，合作交流，实践探索二，典型例题，检测反馈等内容，欢迎下载使用。

圆是中心对称图形,圆心是它的对称中心。
摩天轮绕固定轴心旋转 180度，它都与初始位置重合吗？
圆有旋转不变性：圆绕圆心旋转任何角度后都能与原来的图形重合。
2.思考： 回顾上节课所学内容，什么是等弧？我们用什么方法验证两条弧是等弧？
能够互相重合的弧叫等弧。
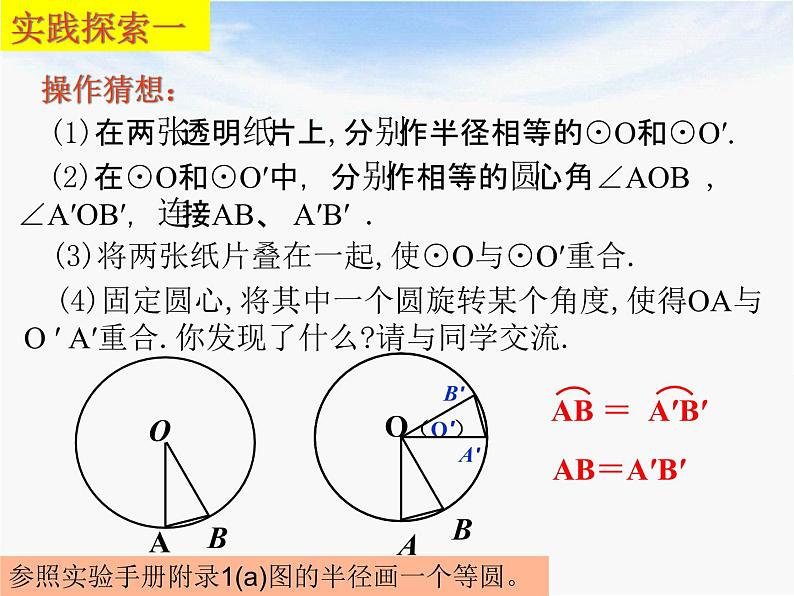
(1)在两张透明纸片上,分别作半径相等的⊙O和⊙O′.
　(2)在⊙O和⊙O′中，分别作相等的圆心角∠AOB ,∠A′OB′，连接AB、 A′B′ .
(3)将两张纸片叠在一起,使⊙O与⊙O′重合.
　(4)固定圆心,将其中一个圆旋转某个角度,使得OA与O ′ A′重合.你发现了什么?请与同学交流.
参照实验手册附录1(a)图的半径画一个等圆。
证明：当OA与O′A′重合时，
∵∠AOB＝∠A′O′B′，
∴OB与O′B′重合.
又∵OA＝O′A′，OB＝O′B′，
∴点A与点A′重合，点B与点B′重合.
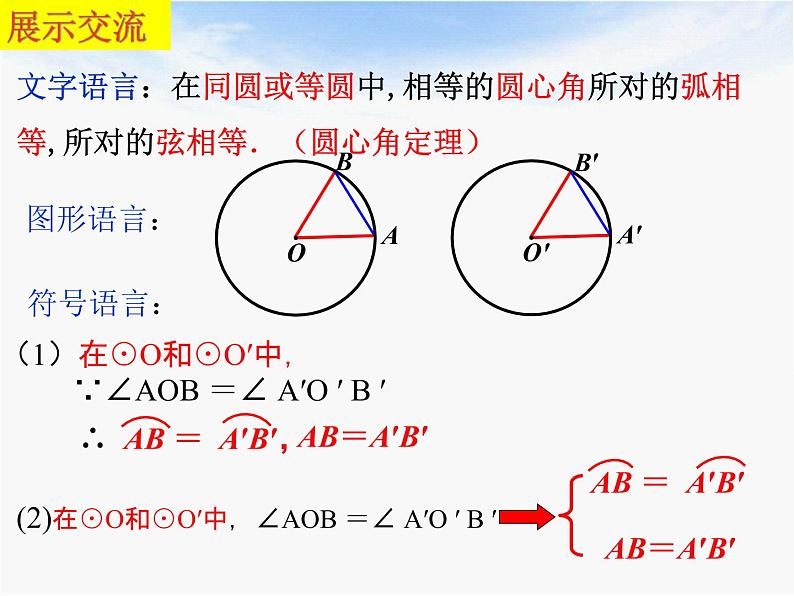
文字语言：在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等．（圆心角定理）
∵∠AOB ＝∠ A′O ′ B ′
（1）在⊙O和⊙O′中，
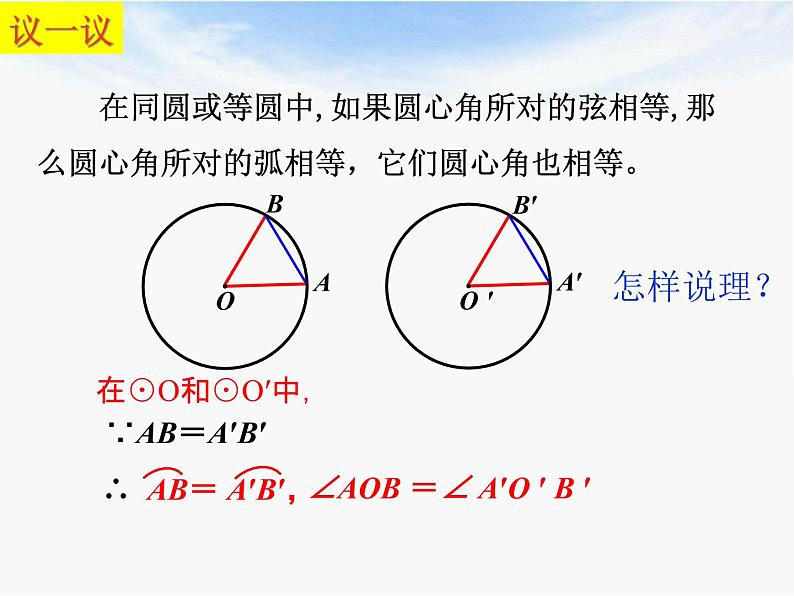
在同圆或等圆中,如果圆心角所对的弧相等,那么它们所对的弦相等，这两个圆心角相等。
∠AOB ＝∠ A′O ′B ′
把圆心角定理的条件与其中一个结论互换，你能得到什么命题？是真命题吗？为什么？
在同圆或等圆中,如果圆心角所对的弦相等,那么圆心角所对的弧相等，它们圆心角也相等。
∠AOB ＝∠ A′O ′ B ′
在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
1．因为∠AOB＝∠ A′O ′B ′，所以
∠AOB＝∠ A′O′ B′.
3．因为AB＝A′B′,所以
圆心角的度数与它所对的弧的度数相等.
判断：圆心角与它所对的弧相等。（ ）
　　例1　如图, AB、AC、BC都是⊙O的弦,∠AOC＝∠BOC.∠ABC与∠BAC相等吗？为什么？
解： ∠ABC与∠BAC相等。
在⊙O中， ∵ ∠AOC＝∠BOC
∴ ∠ABC=∠BAC
（从已知着手，或从问题入手）
　　1．如图1,在⊙O中,AC＝BD,∠AOB＝50º,求∠COD的度数.
　　2．如图2,在⊙O中, AB＝ AC ,∠A＝40º，求∠ABC的度数.
　 3.如图3,在△ABC中, ∠C＝90°, ∠B＝28°,以C为圆心,CA为半径的圆交AB于点D,交BC与点E．求AD、DE的度数.
如图,在同圆中,若AB＝2CD,则AB与2CD的大小关系是( )．
　　A．AB＞2CD B．AB＜2CD 　　C． AB＝2CD D．不能确定
通过这节课的学习，你有哪些收获？又有哪些体会与同学们共享？我知道了……　我学会了……　我体会了……
你感受到什么数学方法？
必做题：教材P48T2, P49T3选做题：教材P49T4