湘教版八年级上册2.3 等腰三角形公开课ppt课件

这是一份湘教版八年级上册2.3 等腰三角形公开课ppt课件，文件包含232等腰三角形的判定-课件pptx、232等腰三角形的判定-教学设计docx、232等腰三角形的判定-试卷docx等3份课件配套教学资源，其中PPT共23页， 欢迎下载使用。

2、等腰三角形都有哪些性质呢？
等腰三角形两边相等（定义）；
等腰三角形两底角相等（性质定理）；
等腰三角形底边上的高、底边上的中线与顶角的平分线互相重合（三线合一）；
等腰三角形是有两边相等的三角形.
1、什么是等腰三角形？
等边三角形每个角都相等并且每个角都等于60°。
等腰三角形是轴对称图形，对称轴是顶角平分线所在的直线；等边三角形有三条对称轴.
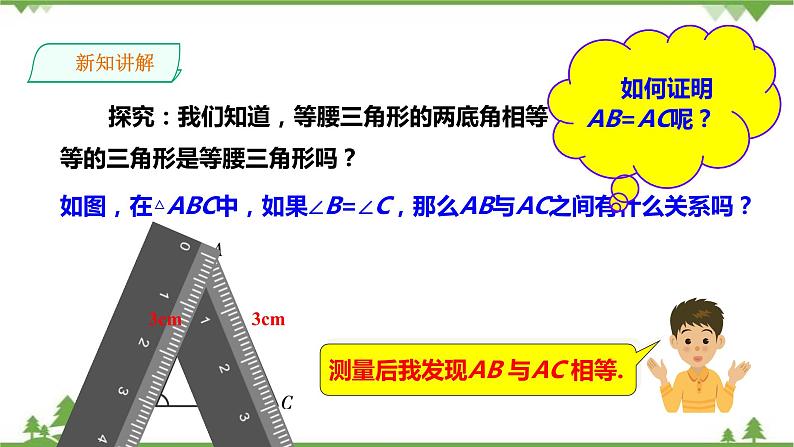
测量后我发现AB 与AC 相等.
探究：我们知道，等腰三角形的两底角相等，反过来，两个角相等的三角形是等腰三角形吗？
如图，在△ABC中，如果∠B=∠C，那么AB与AC之间有什么关系吗？
请用格尺量一量它们的长度，你发现了什么！
如何证明AB=AC呢？
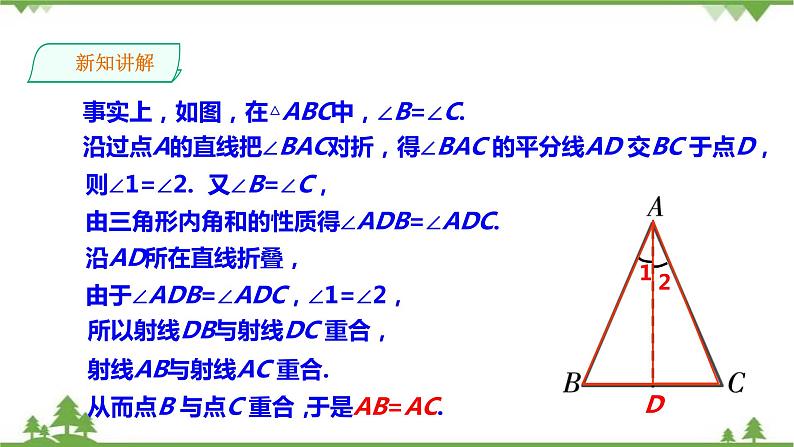
事实上，如图，在△ABC中，∠B=∠C.
沿过点A的直线把∠BAC对折，得∠BAC 的平分线AD 交BC 于点D，
由三角形内角和的性质得∠ADB=∠ADC.
由于∠ADB=∠ADC，∠1=∠2，
所以射线DB与射线DC 重合，
射线AB与射线AC 重合.
从而点B 与点C 重合，
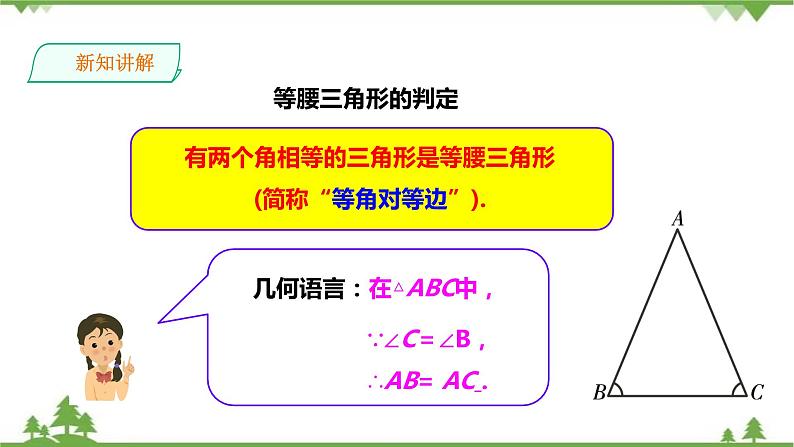
有两个角相等的三角形是等腰三角形(简称“等角对等边”).
∵∠C＝∠B，∴AB= AC .
几何语言：在△ABC中，
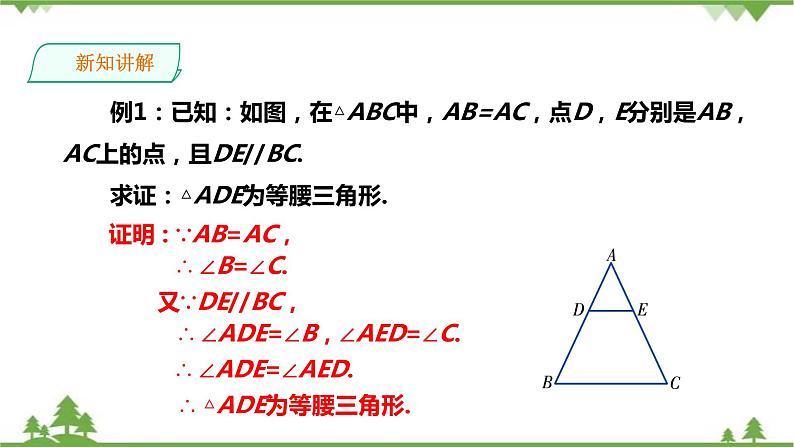
例1：已知：如图，在△ABC中，AB=AC，点D，E分别是AB，AC上的点，且DE//BC.求证：△ADE为等腰三角形.
证明 : ∵AB=AC，
∴ ∠ADE=∠B，∠AED=∠C.
∴ ∠ADE=∠AED.
∴ △ADE为等腰三角形.
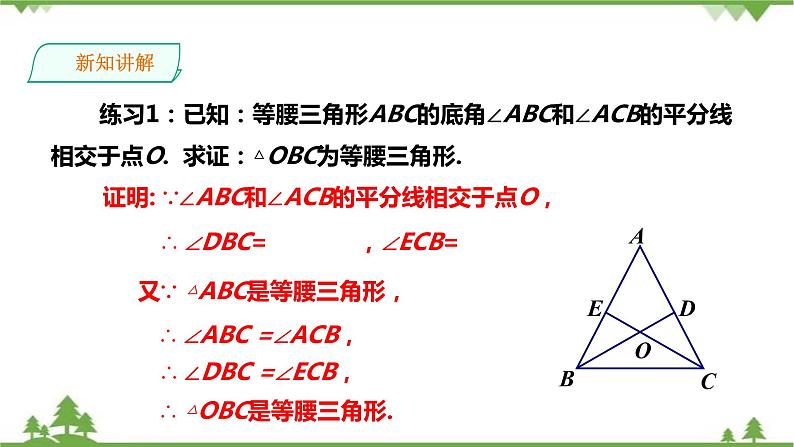
练习1：已知：等腰三角形ABC的底角∠ABC和∠ACB的平分线相交于点O. 求证：△OBC为等腰三角形.
证明: ∵∠ABC和∠ACB的平分线相交于点O，
∴ ∠DBC= ，
又∵ △ABC是等腰三角形，
∴ ∠DBC =∠ECB，
∴ △OBC是等腰三角形.
∴ ∠ABC =∠ACB，
思考1：三个角都是60°的三角形是等边三角形吗？
已知：在△ABC 中， ∠A =∠B =∠C =60°．求证：△ABC是等边三角形．
证明： ∵∠C=∠B =60°， ∴AB =AC ， 同理可证： AB＝BC，AC＝BC， ∴AB=BC =AC． ∴△ABC 是等边三角形．
三个角都是60°的三角形是等边三角形.
∵∠A=∠B =∠C ＝60° ， ∴△ABC 是等边三角形．
练习2：已知：如图，CD平分∠ACB，AE//DC，AE交BC的延长线于点E，且∠ACE= 60°. 求证：△ACE是等边三角形.
∴ ∠CAE= 180°- ∠E -∠ACE =60 °
∴ ∠BCD=∠E=60°，
∴ ∠ACD =∠DCB，
∴ ∠ACD=∠DCB=60°，
∴ ∠CAE = ∠ACE=∠E=60°
∴△ACE是等边三角形.
思考2：一个等腰三角形的一个内角满足什么条件才是等边三角形呢？
已知：在△ABC 中，AB =AC且∠A =60°．求证：△ABC是等边三角形．
证明：∵AB =AC，∴∠B =∠C ，∵∠A =60°，∴∠B =∠C =60°，∴∠A =∠B =∠C，∴AB=BC =AC．∴△ABC 是等边三角形．
有一个角是60°的等腰三角形是等边三角形
∵AB =AC，∠A =60°，∴△ABC 是等边三角形．
有一个角等于60 °的三角形是等边三角形吗？
例2：已知：如图，△ABC是等边三角形，点D，E分别在BA，CA的延长线上，且AD=AE. 求证：△ADE是等边三角形.
证明 ∵△ABC是等边三角形，
∴∠BAC=∠B=∠C= 60°.
∵∠EAD=∠BAC= 60°，
∴△ADE是等边三角形
（ ）
练习3：已知：如图，AB=BC, ∠CDE= 120°, DF∥BA，且DF平分∠CDE，AE交BC的延长线于点E，且∠ACE= 60°. 求证：△ABC是等边三角形.
证明：∵AB=BC，∴ △ABC是等腰三角形，∵∠CDE=120°，且DF平分∠CDE，∴∠CDF= =60° 又∵DF∥BA,∴∠ABC= ∠FDC=60°∴△ABC是等边三角形.
1．如图，在△ABC中，BD⊥AC，∠A＝50°，∠CBD＝25°，若AC＝6 cm，则AB＝________．
证明：∵△ABC 是等边三角形，∴∠A =∠B =∠C =60°．∵DE//BC，∴∠B=∠ADE，∠C =∠AED．∴∠A=∠ADE =∠AED．∴△ADE 是等边三角形．
　　2.如图，△ABC 是等边三角形，DE//BC, 分别交AB，AC 于点D，E． 求证：△ADE 是等边三角形.
如图， △ ABC中,∠ACB的平分线交AB于点E,过点E作FE//BC,交AC于点O,交∠ACD的平分线于点F,求证：EO=FO.
证明： ∵CE平分∠ACB，CF平分∠ACD，
∴∠1=∠2，∠3=∠4.
∴ ∠2=∠5，∠3=∠6,
∴ ∠1=∠5，∠4=∠6,
∴EO=CO,FO=CO,
1. 这节课我们主要研究的是什么？怎么研究的？
等腰三角形的判定、等边三角形的判定.
2. 你有哪些收获？还存在什么困惑？
定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等(等角对等边）。推论1：三个角相等的三角形是等边三角形。推论2：有一个角等于60°的等腰三角形是等边三角形
课题：2.3.2等腰三角形的判定 
1.等腰三角形的判定： 等角对等边。2.推论1：三个角相等的三角形是等边三角形。3.推论2：有一个角等于60°的等腰三角形是等边三角形
基础作业教材第66页习题2.3A组第4、5、6、7题能力作业教材第67页习题2.3B组第10题