



初中数学2.5 全等三角形完整版ppt课件
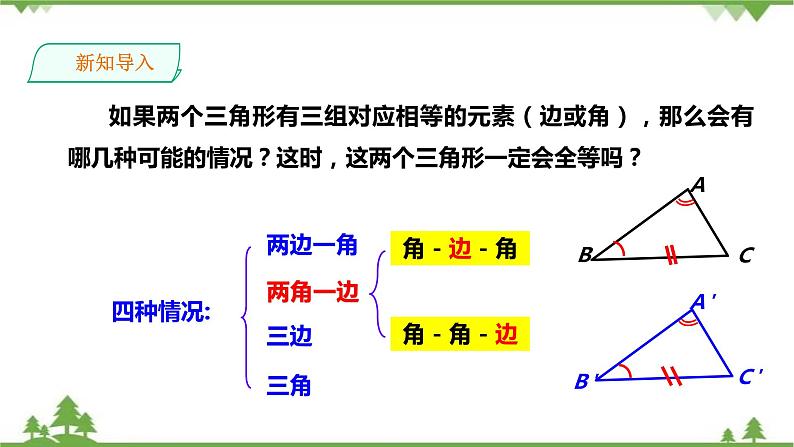
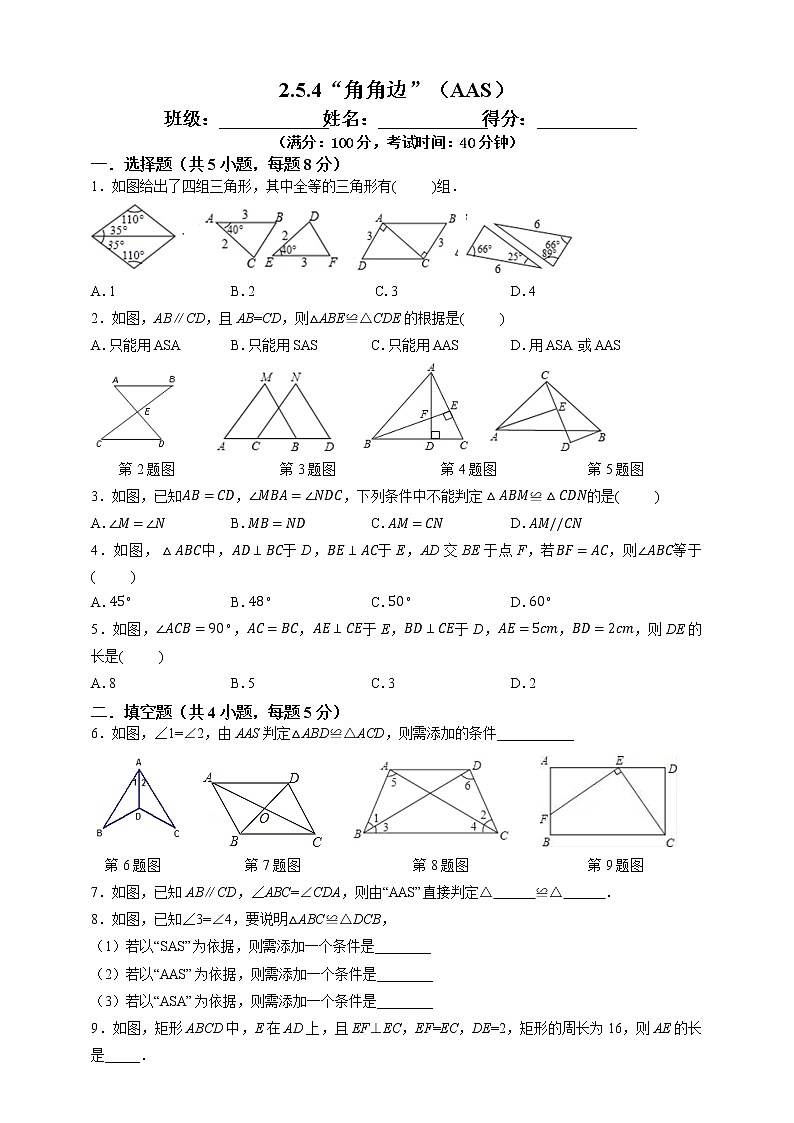
展开说一说全等三角形判定方法?
(1)两边及其夹角分别相等的两个三角形全等.
简写“边角边”或“SAS”.
(2)两角及其夹边分别相等的两个三角形全等.
简写“角边角”或“ASA”.
如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗?
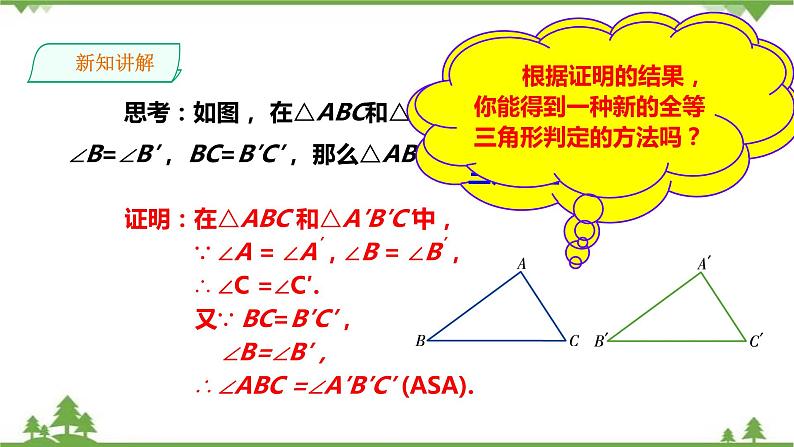
证明:在△ABC 和△A′B′C′中,∵ ∠A = ∠A′,∠B = ∠B′,∴ ∠C =∠C′.又∵ BC=B′C′, ∠B=∠B′,∴ ∠ABC =∠A′B′C′ (ASA).
思考:如图, 在△ABC和△A′B′C′中, 如果∠A=∠A′, ∠B=∠B′, BC=B′C′, 那么△ABC 和△A′B′C′全等吗?
根据三角形内角和定理,你能将上述条件转化为满足“ASA”的条件,从而证明这两个三角形全等吗?
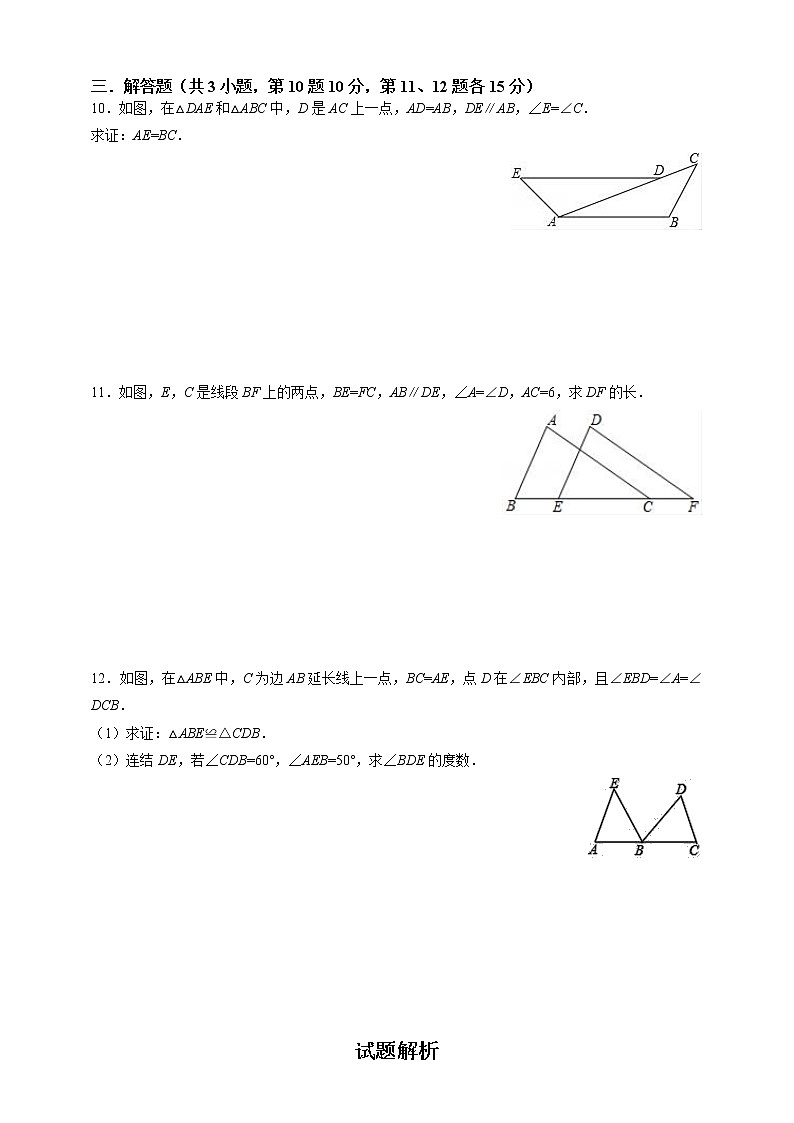
根据证明的结果,你能得到一种新的全等三角形判定的方法吗?
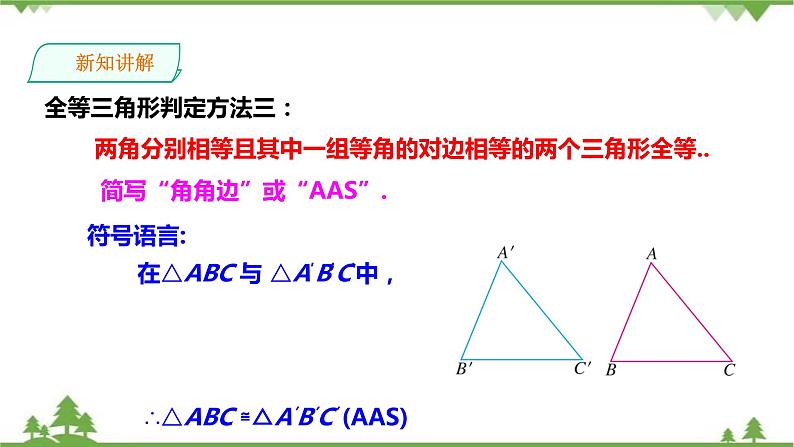
全等三角形判定方法三:
两角分别相等且其中一组等角的对边相等的两个三角形全等..
简写“角角边”或“AAS”.
在△ABC 与 △A′B′C′中,
∴△ABC ≌△A′B′C′ (AAS)
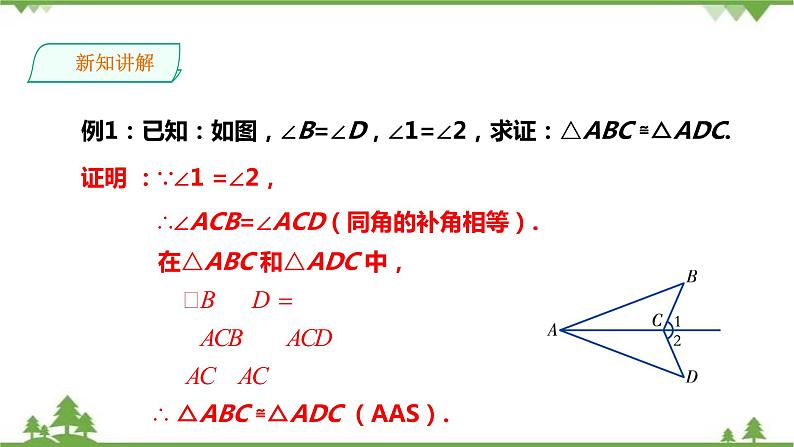
例1:已知:如图,∠B=∠D,∠1=∠2,求证:△ABC ≌△ADC.
证明 :∵∠1 =∠2,
∴∠ACB=∠ACD(同角的补角相等).
在△ABC 和△ADC 中,
∴ △ABC ≌△ADC (AAS).
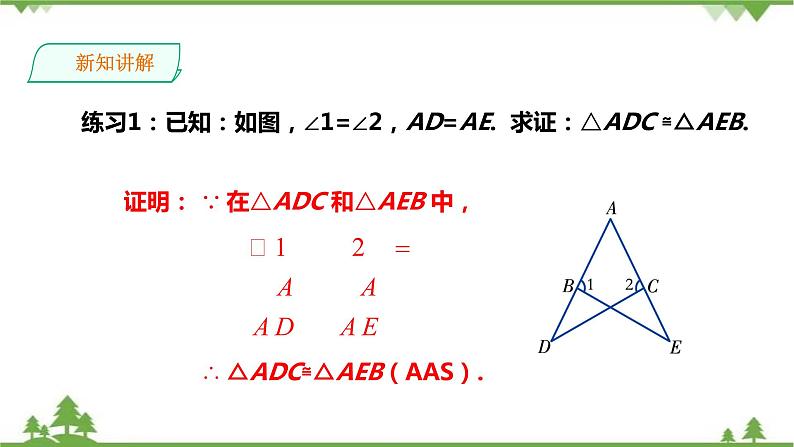
练习1:已知:如图,∠1=∠2,AD=AE. 求证:△ADC ≌△AEB.
∴ △ADC≌△AEB(AAS).
∵ 在△ADC 和△AEB 中,
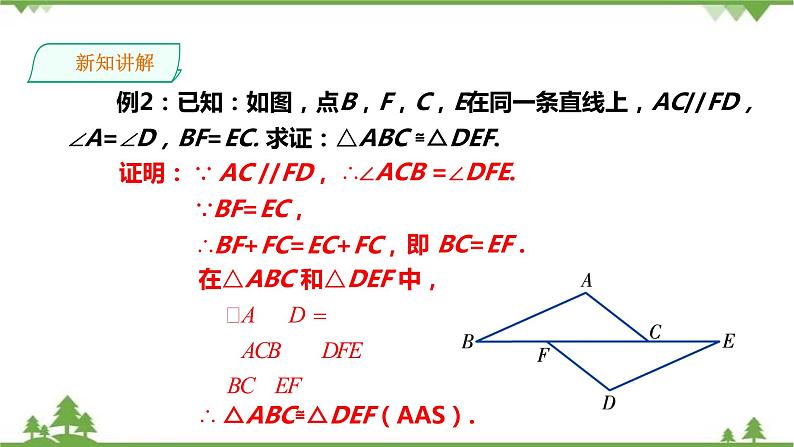
例2:已知:如图,点B,F,C,E在同一条直线上,AC//FD,∠A=∠D,BF=EC. 求证:△ABC ≌△DEF.
证明: ∵ AC //FD,
∴∠ACB =∠DFE.
∴BF+FC=EC+FC,
在△ABC 和△DEF 中,
∴ △ABC≌△DEF(AAS).
练习2:已知:在△ABC中,∠ABC =∠ACB, BD⊥AC于点D,CE⊥AB 于点E. 求证:BD=CE.
证明: 由题意可知△BEC 和△BDC 均为直角三角形,
在Rt△BEC 和Rt△CDB 中,
∴ Rt△BEC≌ Rt△CDB(AAS).
1.如图,∠B=∠DEF,AB=DE,要判断△ABC≌△DEF,(1)若以“ASA”为依据,还需添加的条件为________________ ;(2)若以“AAS”为依据,还需添加的条件为_____________________.
2.如图,在△ABC中,∠B=∠C,D为BC的中点,过点D分别向AB,AC作垂线段,则能够直接判断△BDE≌△CDF的理由是( )A.SSSB.SAS C.ASA D.AAS
3.如图,将长方形纸片ABCD沿BD折叠得到△BDC′,则图中(包括实线、虚线在内)共有全等三角形( )A.2对 B.3对 C.4对 D.5对
4.如图,能够判定全等的两个三角形是( ) A.①和② B.②和④ C.①和③ D.③和④
5.如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC 和△ADE全等吗?为什么?
解: △ABC 和△ADE 全等. 理由如下: ∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC 即∠BAC=∠DAE 在△ABC 和△ADC 中
∴ △ABC≌△ADE(AAS)
如图,BD⊥AC于点D, CE⊥AB于点E, BD=CE. 求证BE=CD.
证明:∵BD⊥AC于点D,CE⊥AB于点E, ∴∠ADB=∠AEC=90°.
∴△ABD≌△ACE(AAS). ∴AB=AC, AD=AE,∴AB-AE=AC-AD,即BE=CD.
在△ABD和△ACE中,
1. 这节课我们主要研究的是什么?怎么研究的?
利用角角边这一定理判定两个三角形全等.
2. 你有哪些收获?还存在什么困惑?
两角和其中一角的对边对应相等的两个三角形全等. 简称“角角边”或“AAS”.判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到.
课题:2.5.4“角角边”(AAS)
三角形全等的判定方法3:两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.
基础作业教材第87页习题2.5A组第5题能力作业教材第88页习题2.5B组第11题
初中数学人教版八年级上册12.2 三角形全等的判定教学ppt课件: 这是一份初中数学人教版八年级上册12.2 三角形全等的判定教学ppt课件,共45页。PPT课件主要包含了学习目标,新课引入,新知学习,课堂小结,SSS,SAS,△ABE≌△ACD,第1题图,第3题图,第4题图等内容,欢迎下载使用。
人教版八年级上册12.1 全等三角形优秀ppt课件: 这是一份人教版八年级上册12.1 全等三角形优秀ppt课件,文件包含1223全等三角形的判定ASAAAS教学课件pptx、人教数学八上122三角形全等的判定第3课时学案+练习docx、第十二章122三角形全等的判定第3课时教学详案docx等3份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
初中数学湘教版八年级上册2.5 全等三角形优秀ppt课件: 这是一份初中数学湘教版八年级上册2.5 全等三角形优秀ppt课件,文件包含湘教版8上数学第二章254《全等三角形判定SSS》课件ppt、湘教版8上数学第二章254《全等三角形判定SSS》教案docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。













