




数学第5章 一次函数综合与测试精品随堂练习题
展开第5章 一次函数
一次函数 章末复习
知识提要
1. 常量与变量:在一个过程中,固定不变的量称为常量,可以取不同数值的量称为变量.
2. 函数:一般地,在某个变化过程中,设有两个变量x,y,如果对于x的每一个确定的
3. 一次函数与正比例函数:一般地,函数y=kx+b(k,b都是常数,且k≠0)叫做一次函数.当b=0时,一次函数y=kx+b就成为y=kx,叫做正比例函数,常数k叫做比例系数.
4. 一次函数的图象及其性质
典型例题
例1:在同一坐标系中,一次函数y=ax+b和一次函数y=bx+a图象可以是 ( B )
A B C D
例2:如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1
解析:由图象可知,当x<1时,直线y1落在直线y2的下方,
故使y1<y2的x的取值范围是:x<1.
例3:已知一次函数y=-x+2.
(1)到x轴距离为1的点的坐标为___________________;
(2)这个图象上的一点M到x轴的距离是它到y轴距离的两倍,则点M的坐标为__________________.
解析:(1)直线y=-x+2,与x轴的距离为1的点的纵坐标为1或-1,∴-x+2=1或-1,∴x=2或6,∴(2,1)或(6,-1).
(2)由题可设该点坐标为(m,2m)或(m,-2m),分别代入直线y=-x+2,得-m+2=2m或-m+2=-2m,∴m=或-,∴或.
练习
一、 选择题
1. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数
y=kx+k的图象经过的象限为( A )
A.二、三、四 B.一、二、四 C.一、三、四 D.一、二、三
【解析】A ∵正比例函数y=kx的函数值y随x的增大而减小,∴k<0,∵b=k<0,∴一次函数y=kx+k的图象经过二、三、四象限.
2.已知:将直线y=x-1向上平移2个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( )
A.经过第一、二、四象限 B.与x轴交于(1,0)
C.与y轴交于(0,1) D.y随x的增大而减小
【解析】 将直线y=x-1向上平移2个单位后得到的直线表达式为y=x-1+2,即y=x+1,当x=0时,y=1,∴与y轴交于点(0,1);当y=0时,x=-1,与x轴交于点(-1,0);图象经过第一、二、三象限;y随x的增大而增大.故选C.
3. 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图1中折线表示小强离开家的路程y(km)和所用时间x(min)之间的函数关系.下列说法中错误的是( D )
A. 小强从家到公共汽车站步行了2 km
B.小强在公共汽车站等小明用了10 min
C.公共汽车的平均速度是30 km/h
D.小强乘公共汽车用了20 min
【解析】 图象的第一段表示小强步行到车站,用时20 min,步行了2 km;第二段表示小强在车站等小明,用时30-20=10(min),此段时间行程为0;第三段表示两个人一起乘公共汽车到学校,用时60-30=30(min)=0.5(h),此段时间的行程为17-2=15(km),公共汽车的平均速度为15÷0.5=30(km/h).故选D.
4. 如图,直线y=kx+b(k≠0)经过点A(-2,4),则不等式kx+b>4的解集为 ( A )
A.x>-2 B.x<-2 C.x>4 D.x<4
5. 若直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为 ( B )
A.(-2,0) B.(2,0) C.(-6,0) D.(6,0)
【解析】B (0,4)关于x轴的对称点为(0,-4),(3,2)关于x轴的对称点为(3,-2),则l1经过(0,4)和(3,-2),l2经过(0,-4)和(3,2),通过待定系数法可得两条直线的表达式分别为y1=-2x+4,y2=2x-4,联立方程组,解得x=2,y=0.∴交点坐标为(2,0).
6. 已知一次函数y=kx+b-x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )
A.k>1,b<0 B.k>1,b>0 C.k>0,b>0 D.k>0,b<0
解析:一次函数y=kx+b-x即为y=(k-1)x+b,∵函数值y随x的增大而增大,∴k-1>0,解得k>1;∵图象与x轴的正半轴相交,∴图象与y轴的负半轴相交,∴b<0.
7. 关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
A.点(0,k)在l上 B.l经过定点(-1,0)
C.当k>0时,y随x的增大而增大 D.l经过第一、二、三象限
解析:A.当x=0时,y=k,即点(0,k)在l上,故此选项正确;B.当x=-1时,y=-k+k=0,此选项正确;C.当k>0时,y随x的增大而增大,此选项正确;D.不能确定l经过第一、二、三象限,此选项错误.
8. 点P1(x1,y1),P2(x2,y2)是一次函数y=kx+b(k<0)图象上的两个点,且x1
9. 如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),直线y=2x过点A,则不等式2x
A.x<-2 B.-2
10. 甲、乙两地相距80 km,一辆汽车上午9:00从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了20 km/h,并继续匀速行驶至乙地,汽车行驶的路程y(km)与时间x(h)之间的函数关系如图所示,该车到达乙地的时间是当天上午 ( B )
A.10:35 B.10:40 C.10:45 D.10:50
【解析】 由图象知,汽车行驶前一半路程(40 km)所用的时间是1 h,
∴速度为40÷1=40(km/h),于是行驶后一半路程的速度是40+20=60(km/h),
∴行驶后一半路程所用的时间为40÷60=(h),∵ h=×60 min=40 min,
∴该车一共行驶了1小时40分钟到达乙地,∴到达乙地的时间是当天上午10:40.
11. [a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”[1,m-]的一次函数是正比例函数,则关于x的方程x+=的解为( C )
A. B.- C. D.-
【解析】 由题意得[1,m-]为正比例函数y=x+m-的“关联数”,即m-=0,解得m=,代入关于x的方程x+=,得x+=,解得x=.
12. 若直线y=-2x-4与直线y=4x+b的交点在第三象限,则b的取值范围是( A )
A.-4<b<8 B.-4<b<0 C.b<-4或b>8 D.-4≤b≤8
解析:,解得:,∵交点在第三象限,∴-<0,<0,
解得:b>-4,b<8,∴-4<b<8.
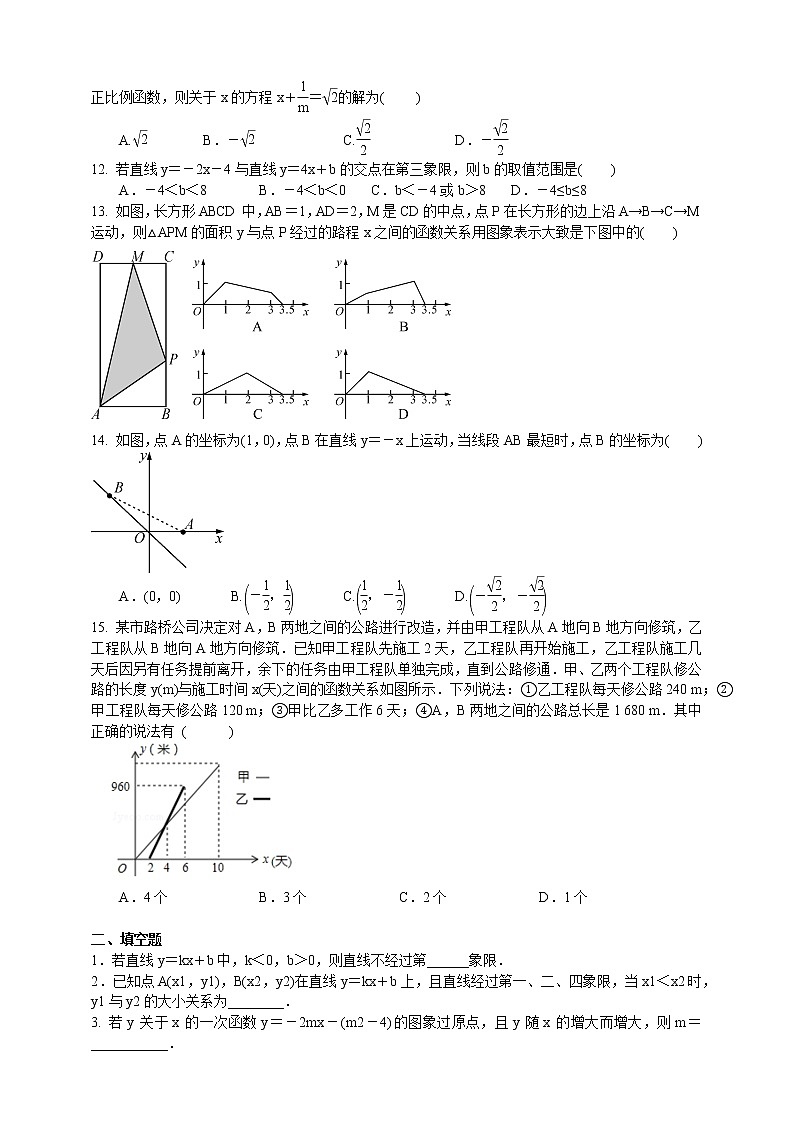
13. 如图,长方形ABCD中,AB=1,AD=2,M是CD的中点,点P在长方形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( A )
解析:点P由A到B这一段中,三角形的AP边上的高不变,因而面积是路程x的正比例函数,当P到达B点时,面积达到最大,值是1.在P由B到C这一段,面积随着路程的增大而减小;到达C点,即路程是3时,最小是;由C到M这一段,面积越来越小;当P到达M时,面积最小变成0.因而应选第一个图象.
14. 如图,点A的坐标为(1,0),点B在直线y=-x上运动,当线段AB最短时,点B的坐标为( )
A.(0,0) B. C. D.
解析:过A点作垂直于直线y=-x的垂线AB,∵点B在直线y=-x上运动,
∴∠AOB=45°,∴△AOB为等腰直角三角形,过B作BC垂直x轴垂足为C,
则点C为OA的中点,则OC=BC=.作图可知B在x轴下方,y轴的右方.
∴横坐标为正,纵坐标为负.所以当线段AB最短时,点B的坐标为.
15. 某市路桥公司决定对A,B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A地方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度y(m)与施工时间x(天)之间的函数关系如图所示.下列说法:①乙工程队每天修公路240 m;②甲工程队每天修公路120 m;③甲比乙多工作6天;④A,B两地之间的公路总长是1 680 m.其中正确的说法有 ( B )
A.4个 B.3个 C.2个 D.1个
【解析】 ①乙工程队每天修公路=240 m,正确;
②甲工程队每天修公路=120 m,正确;
③甲比乙多工作10-4=6天,正确;
④A,B两地之间的公路总长是960+120×10=2 160 m,错误;故选B.
二、填空题
1.若直线y=kx+b中,k<0,b>0,则直线不经过第__三____象限.
2.已知点A(x1,y1),B(x2,y2)在直线y=kx+b上,且直线经过第一、二、四象限,当x1<x2时,y1与y2的大小关系为y1>y2________.
【解析】 由于一次函数图象经过二、四象限,
∴k<0,y随x的增大而减小,
∴当x1<x2时,y1>y2.
3. 若y关于x的一次函数y=-2mx-(m2-4)的图象过原点,且y随x的增大而增大,则m=-2___________.
解析:由题意得
∴m=-2.
4.如图,直线y=kx+b过A(-1,2),B(-2,0)两点,则0≤kx+b≤-2x的解集为-2≤x≤-1________________.
【解析】 由已知得直线OA的表达式为y=-2x,如图,当-2≤x≤-1时,0≤kx+b≤-2x.
5. 函数y1=2x-1与y2=3+x的图象的交点坐标为(4,7)______,当x<4_____时,y1
解不等式2x-1<3+x,得x<4.
6. 在函数y=+中,自变量x的取值范围是x≥0且x≠_______________________.
7.若点P(m-2,m)在直线y=-x上,则点(-|m|,m-1)关于y轴的对称点坐标是_________.
解析:由题意得-(m-2)=m,解得m=1,∴点(-|m|,m-1)为(-1,1),∴关于y轴的对称点为(1,1).
8.已知直线y=2x+(3-a)与x轴的交点在A(2,0),B(3,0)之间(包括A,B两点),则a的取值范围是7≤a≤9 ______________.
解析:∵直线y=2x+(3-a)与x轴的交点在A(2,0)、B(3,0)之间(包括A、B两点),∴2≤x≤3,令y=0,则2x+(3-a)=0,解得x=,则2≤≤3,解得7≤a≤9.
9. 若点M(k-1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(k-1)x+k的图象不经过第一______象限.
【解析】 ∵点M(k-1,k+1)关于y轴的对称点在第四象限内,
∴点M(k-1,k+1)位于第三象限,∴k-1<0且k+1<0,解得k<-1,
∴一次函数y=(k-1)x+k经过第二、三、四象限,不经过第一象限.
10. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则Bn的坐标是
(2n-1,2n-1)______________________________.(n为正整数)
【解析】 当x=0时,y=x+1=1,∴点A1的坐标为(0,1).
∵四边形A1B1C1O为正方形,∴点B1的坐标为(1,1).当x=1时,y=x+1=2,
∴点A2的坐标为(1,2).∵四边形A2B2C2C1为正方形,∴点B2的坐标为(3,2).同理,可得点A3的坐标为(3,4),点B3的坐标为(7,4),…点An的坐标为(2n-1-1,2n-1),点Bn的坐标为(2n-1,2n-1).
三、解答题
1.已知一次函数y=(3-k)x+2k+1.
(1)若图象经过(-1,2),求k;
(2)若图象经过第一、二、四象限,求k的取值范围.
解:(1)∵一次函数y=(3-k)x+2k+1的图象经过(-1,2),∴2=(3-k)×(-1)+2k+1,即2=3k-2,解得k=;
(2) ∵一次函数y=(3-k)x+2k+1的图象经过一、二、四象限,
∴,解得,k>3.故k的取值范围是k>3.
2.如图,直线y=2x+2与x轴相交于点A,与y轴相交于点B.
(1)求A,B两点的坐标;
(2)过点A作直线AP与y轴相交于P,且使OP=OA,求直线AP的表达式.
解:(1)在y=2x+2中,当x=0时,y=2;当y=0时,x=-1.
∴A(-1,0),B(0,2);
(2)∵A(-1,0),∴OA=1,∵OP=OA,∴OP=1,
∵P在y轴上,∴P(0,1)或P(0,-1).
设直线AP的表达式为y=kx+b.则由题意,得或
解得或
∴直线AP的表达式是y=x+1或y=-x-1.
3. 如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的表达式;
(2)求△AOB的面积.
解:(1)把A(-2,-1),B(1,3)代入y=kx+b,得解得
∴一次函数的表达式为y=x+;
(2)把x=0代入y=x+,得y=,∴D点坐标为,
∴S△AOB=S△AOD+S△BOD=××2+××1=.
4.在直角坐标系中,点A,点B,点C坐标分别为A(4,0),B(8,0),C(0,-4).
(1)求过B,C两点的一次函数解析式;
(2)若直线BC上有一动点P(x,y),以点O,A,P为顶点的三角形面积和以点O,C,P为顶点的三角形面积相等,求P点坐标.
解:(1)设直线BC的解析式为:y=kx+b,
∵点B、点C坐标分别为(8,0)、(0,-4).
∴,解得:,
故过B、C两点的一次函数解析式为:y=x-4;
(2)设P的坐标为:,∵点A、点C坐标分别为(4,0)、(0,-4).∴OA=OC=4,∵以点O、A、P为顶点的三角形面积和以点O、C、P为顶点的三角形面积相等,
∴=|x|,即x-4=x或x-4=-x,
解得:x=-8或x=,故P的坐标为:(-8,-8)或.
5.如图直线m与x轴、y轴分别交于点B(-4,0)和A(0,3).
(1)请求出直线m的表达式;
(2)在坐标轴上是否存在一点C,使△ABC为等腰三角形?若存在,请直接写出点C的坐标(不需要具体的解题过程)(至少3个);若不存在,请说明理由.
解:(1)设y=kx+b(k≠0),由题意,得得,∴y=0.75x+3.
(2)当C在x轴上时,设C(x,0).∵△ABC是等腰三角形,
∴①当CA=CB时,=,解得x=-,∴C;
②当AB=AC时,=,解得x=±4,∵C点与B点不重合,∴C(4,0);
③当AB=BC时,=,解得,x=-9或x=1,∴C(-9,0)或(1,0).当C在y轴上时,设C(0,y),同理可以求得C(0,8),(0,-3),(0,-2),(0,-).∴所有符合条件的点C的坐标是(-,0),(4,0),(-9,0),(1,0),(0,8),(0,-3),(0,-2),(0,-).
6.小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲跑步中途改为步行,到达图书馆恰好用30 min.小东骑自行车以300 m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示.
(1)家与图书馆之间的路程为4000________m,小玲步行的速度为_100______m/min;
(2)求小东离家的路程y关于x的函数表达式,并写出自变量的取值范围;
(3)求两人相遇的时间.
解:(2)∵小东从图书馆到家的时间x==(h),∴D.设CD的表达式为y=kx+b(k≠0),
∵图象经过C(0,4 000),D两点,∴解得
∴y=-300x+4 000,
∴小东离家的路程y与x的表达式为y=-300x+4 000;
(3)设OA的表达式为y=mx(m≠0),
∵图象过点A(10,2 000),∴10m=2 000,解得m=200,
∴OA的表达式为y=200x(0≤x≤10),
∴解得
答:两人出发8 min相遇.
7.如图,直线l1:y1=-x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=x+b过点P.
(1)求点P坐标和b的值;
(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t s.
①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;
②求出t为多少时,△APQ的面积小于3;
③是否存在t的值,使△APQ为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
解:(1)∵点P(m,3)为直线l1上一点,∴3=-m+2,解得m=-1,
∴点P的坐标为(-1,3),把点P的坐标代入y2=x+b,得3=×(-1)+b,解得b=,
(2)∵b=,∴直线l2的表达式为y=x+,∴C点的坐标为(-7,0),
①由直线l1:y1=-x+2可知A(2,0),∴当Q在A,C之间时,AQ=2+7-t=9-t,
∴S=AQ·|yP|=×(9-t)×3=-t;
当Q在A的右边时,AQ=t-9,∴S=AQ·|yP|=×(t-9)×3=t-;
即△APQ的面积S与t的函数关系式为S=
②∵S<3,∴-t+<3或t-<3,解得7<t<9或9<t<11.
③存在.设Q(t-7,0),
当PQ=PA时,则(t-7+1)2+(0-3)2=(2+1)2+(0-3)2,
∴(t-6)2=32,解得t=3或t=9(舍去);
当AQ=PA时,则(t-7-2)2=(2+1)2+(0-3)2,
∴(t-9)2=18,解得t=9+3或t=9-3;
当PQ=AQ时,则(t-7+1)2+(0-3)2=(t-7-2)2,
∴(t-6)2+9=(t-9)2,解得t=6.
故当t的值为3或9+3或9-3或6时,△APQ为等腰三角形.
初中数学5.3 一次函数精品课后作业题: 这是一份初中数学5.3 一次函数精品课后作业题,文件包含第5章一次函数章末复习答案版docx、第5章一次函数章末复习原卷版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
初中数学浙教版八年级上册第5章 一次函数5.5 一次函数的简单应用优秀一课一练: 这是一份初中数学浙教版八年级上册第5章 一次函数5.5 一次函数的简单应用优秀一课一练,文件包含浙教版数学八上同步提高55一次函数的简单应用原卷版docx、浙教版数学八上同步提高55一次函数的简单应用答案版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
浙教版八年级上册5.4 一次函数的图象优秀一课一练: 这是一份浙教版八年级上册5.4 一次函数的图象优秀一课一练,文件包含浙教版数学八上同步提高54一次函数的图象原卷版docx、浙教版数学八上同步提高54一次函数的图象答案版docx等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。













