数学人教A版 (2019)8.6 空间直线、平面的垂直优秀教学设计

这是一份数学人教A版 (2019)8.6 空间直线、平面的垂直优秀教学设计，共20页。教案主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

学习目标 1.理解直线与平面垂直的定义；2.掌握直线与平面垂直的判定定理的内容及其应用；3.应用直线与平面垂直的判定定理解决问题．
知识点一 直线与平面垂直的定义
思考1 在阳光下观察直立于地面的旗杆及它在地面上的影子，随着时间的变化，影子的位置在移动，在各个时刻旗杆所在的直线与其影子所在的直线夹角是否发生变化，为多少？
答案 不变，90°.
知识点二 直线和平面垂直的判定定理
将一块三角形纸片ABC沿折痕AD折起，将翻折后的纸片竖起放置在桌面上(BD，DC与桌面接触)．观察折痕AD与桌面的位置关系．
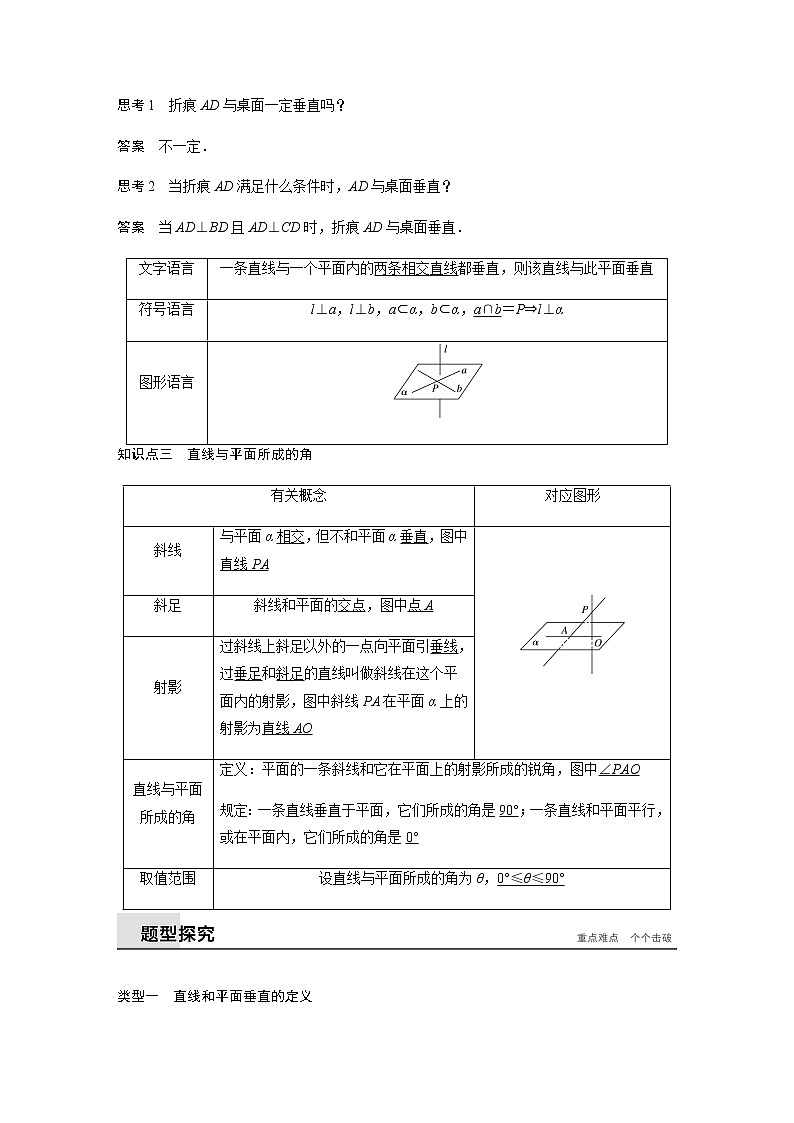
思考1 折痕AD与桌面一定垂直吗？
答案 不一定．
思考2 当折痕AD满足什么条件时，AD与桌面垂直？
答案 当AD⊥BD且AD⊥CD时，折痕AD与桌面垂直．
知识点三 直线与平面所成的角
类型一 直线和平面垂直的定义
例1 下列命题中，正确的序号是________．
①若直线l与平面α内的无数条直线垂直，则l⊥α；
②若直线l与平面α内的一条直线垂直，则l⊥α；
③若直线l不垂直于平面α，则α内没有与l垂直的直线；
④若直线l不垂直于平面α，则α内也可以有无数条直线与l垂直；
⑤过一点和已知平面垂直的直线有且只有一条．
答案 ④⑤
解析 当直线l与平面α内的无数条平行直线垂直时，l与α不一定垂直，所以①不正确；当l与α内的一条直线垂直时，不能保证l与平面α垂直，所以②不正确；当l与α不垂直时，l可能与α内的无数条平行直线垂直，所以③不正确，④正确；过一点有且只有一条直线垂直于已知平面，所以⑤正确．故填④⑤.
反思与感悟 1.直线和平面垂直的定义是描述性定义，对直线的任意性要注意理解．实际上，“任何一条”与“所有”表达相同的含义．当直线与平面垂直时，该直线就垂直于这个平面内的任何直线．由此可知，如果一条直线与一个平面内的一条直线不垂直，那么这条直线就一定不与这个平面垂直．
2．由定义可得线面垂直⇒线线垂直，即若a⊥α，b⊂α，则a⊥b.
跟踪训练1 下面叙述中：
①若直线垂直于平面内的两条直线，则这条直线与平面垂直；
②若直线与平面内的任意一条直线都垂直，则这条直线与平面垂直；
③若直线垂直于梯形的两腰所在的直线，则这条直线垂直于两底边所在的直线；
④若直线垂直于梯形的两底边所在的直线，则这条直线垂直于两腰所在的直线．
其中正确的有( )
A．1个 B．2个 C．3个 D．4个
答案 B
解析 ①中若两条直线为平行直线，则这条直线不一定与平面垂直，所以不正确；②由定义知正确；③中直线与梯形的两腰所在直线垂直，则与梯形所在平面垂直，由定义知也与两底边所在直线垂直，所以正确；④中直线与梯形两底边所在直线垂直，则不一定与梯形所在平面垂直，故不一定与两腰所在直线垂直，不正确．故选B.
类型二 线面垂直的判定
例2 在平面α内有直角∠BCD，AB⊥平面α，求证CD⊥平面ABC.
解 如图所示．
eq \b\lc\ \rc\}(\a\vs4\al\c1(\b\lc\ \rc\}(\a\vs4\al\c1(AB⊥α,CD⊂α))⇒AB⊥CD,∠BCD＝90°⇒BC⊥CD,AB∩BC＝B))⇒CD⊥平面ABC.
反思与感悟 1.使用直线与平面垂直的判定定理的关键是在平面内找到两条相交直线都与已知直线垂直，即把线面垂直转化为线线垂直来解决．
2．线面垂直的定义具有双重作用：判定和性质，证题时常用它作为性质使用，即“如果一条直线垂直于一个平面，那么这条直线就垂直于平面内的任意一条直线”．
跟踪训练2 如图，在三棱锥S－ABC中，∠ABC＝90°，D是AC的中点，且SA＝SB＝SC.
(1)求证：SD⊥平面ABC；
(2)若AB＝BC，求证：BD⊥平面SAC.
证明 (1)因为SA＝SC，D是AC的中点，
所以SD⊥AC.在Rt△ABC中，AD＝BD，
由已知SA＝SB，
所以△ADS≌△BDS，
所以SD⊥BD.又AC∩BD＝D，
所以SD⊥平面ABC.
(2)因为AB＝BC，D为AC的中点，
所以BD⊥AC.由(1)知SD⊥BD.
又因为SD∩AC＝D，所以BD⊥平面SAC.
类型三 直线与平面所成的角
例3 如图，在正方体ABCD­A1B1C1D1中，
(1)求A1B与平面AA1D1D所成的角；
(2)求A1B与平面BB1D1D所成的角．
解 (1)∵AB⊥平面AA1D1D，
∴∠AA1B就是A1B与平面AA1D1D所成的角，
在Rt△AA1B中，∠BAA1＝90°，AB＝AA1，
∴∠AA1B＝45°，
∴A1B与平面AA1D1D所成的角是45°.
(2)连接A1C1交B1D1于点O，连接BO，
∵A1O⊥B1D1，BB1⊥A1O，
∴A1O⊥平面BB1D1D，
∴∠A1BO就是A1B与平面BB1D1D所成的角，
设正方体的棱长为1，∴A1B＝eq \r(2)，A1O＝eq \f(\r(2),2).
又∵∠A1OB＝90°，
∴sin ∠A1BO＝eq \f(A1O,A1B)＝eq \f(1,2)，
∴∠A1BO＝30°.
∴A1B与平面BB1D1D所成的角是30°.
反思与感悟 求斜线与平面所成角的步骤
(1)作图：作(或找)出斜线在平面内的射影，作射影要过斜线上一点作平面的垂线，再过垂足和斜足作直线，注意斜线上点的选取以及垂足的位置要与问题中已知量有关，才能便于计算．
(2)证明：证明某平面角就是斜线与平面所成的角．
(3)计算：通常在垂线段、斜线和射影所组成的直角三角形中计算．
跟踪训练3 如图，在三棱锥ABC­A1B1C1中，∠BAC＝90°，AB＝AC＝2，AA1＝4，A1在底面ABC的射影为BC的中点，D为B1C1的中点．
(1)证明：A1D⊥平面A1BC.
(2)求直线A1B和平面BB1C1C所成的角的正弦值．
解 (1)取BC的中点E，连接A1E，DE，AE，由题意得A1E⊥平面ABC，所以A1E⊥AE，
因为AB＝AC，所以AE⊥BC，故AE⊥平面A1BC，
由D，E分别是B1C1，BC的中点，得DE∥B1B且DE＝B1B，所以DE∥A1A，
所以四边形A1AED是平行四边形，故A1D∥AE，
又因为AE⊥平面A1BC，所以A1D⊥平面A1BC.
(2)作A1F⊥DE，垂足为F，连接BF.因为A1E⊥平面ABC，所以BC⊥A1E.因为BC⊥AE，所以BC⊥平面AA1DE.
所以BC⊥A1F，
A1F⊥平面BB1C1C.
所以∠A1BF为直线A1B与平面BB1C1C所成的角．
由AB＝AC＝2，∠CAB＝90°，
得EA＝EB＝eq \r(2).
由∠A1EA＝∠A1EB＝90°，
得A1A＝A1B＝4，A1E＝eq \r(14).
由DE＝BB1＝4，DA1＝EA＝eq \r(2)，∠DA1E＝90°，
得A1F＝eq \f(\r(7),2).
所以sin ∠A1BF＝eq \f(\r(7),8).
1．空间中直线l和三角形的两边AC，BC同时垂直，则这条直线和三角形的第三边AB的位置关系是( )
A．平行 B．垂直
C．相交 D．不确定
答案 B
解析 由于直线l和三角形的两边AC，BC同时垂直，而这两边相交于点C，所以直线l和三角形所在的平面垂直，又因三角形的第三边AB在这个平面内，所以l⊥AB.
2．直线l⊥平面α，直线m⊂α，则l与m不可能( )
A．平行 B．相交
C．异面 D．垂直
答案 A
解析 若l∥m，l⊄α，m⊂α，
∴l∥α，
这与已知l⊥α矛盾．
所以直线l与m不可能平行．
3．如图①，在正方形SG1G2G3中，E、F分别是边G1G2，G2G3的中点，D是EF的中点，现沿SE、SF及EF把这个正方形折成一个如图②所示的几何体，使G1、G2、G3三点重合于点G，则下面结论成立的是( )
A．SG⊥平面EFG B．SD⊥平面EFG
C．GF⊥平面SEF D．GD⊥平面SEF
答案 A
解析 在图①中，SG1⊥G1E，SG3⊥G3F，因此在图②中，SG⊥GE，SG⊥GF，又GE∩GF＝G，∴SG⊥平面EFG.
4.如图，Rt△BMC中，斜边BM＝5，它在平面ABC上的射影AB长为4，∠MBC＝60°，求MC与平面CAB所成角的正弦值．
解 由题意知，A是M在平面ABC内的射影，
∴MA⊥平面ABC，∴MC在平面CAB内的射影为AC.
∴∠MCA即为直线MC与平面CAB所成的角．
又∵在Rt△BMC中，BM＝5，∠MBC＝60°，
∴MC＝BMsin ∠MBC＝5sin 60°＝5×eq \f(\r(3),2)＝eq \f(5,2)eq \r(3).
在Rt△MAB中，MA＝eq \r(BM2－BA2)＝eq \r(52－42)＝3.
在Rt△MAC中，sin∠MCA＝eq \f(MA,MC)＝eq \f(3,\f(5,2)\r(3))＝eq \f(2,5)eq \r(3).
故MC与平面CAB所成角的正弦值为eq \f(2,5)eq \r(3).
5.如图，已知PA⊥圆O所在平面，AB为圆O的直径，C是圆周上的任意一点，过A作AE⊥PC于E.
求证：AE⊥平面PBC.
证明 ∵PA⊥平面ABC，BC⊂平面ABC，∴PA⊥BC.
∵AC⊥BC，AC∩PA＝A，
∴BC⊥平面PAC.∵AE⊂平面PAC，
∴BC⊥AE.
又∵PC⊥AE，BC∩PC＝C，
PC⊂平面PBC，BC⊂平面PBC，
∴AE⊥平面PBC.
1．线线垂直和线面垂直的相互转化
2．证明线面垂直的方法
(1)线面垂直的定义．
(2)线面垂直的判定定理．
(3)如果两条平行直线的一条直线垂直于一个平面，那么另一条直线也垂直于这个平面．
(4)如果一条直线垂直于两个平行平面中的一个平面，那么它也垂直于另一个平面．
一、选择题
1．下列条件中，能判定直线l⊥平面α的是( )
A．l与平面α内的两条直线垂直
B．l与平面α内的无数条直线垂直
C．l与平面α内的某一条直线垂直
D．l与平面α内的任意一条直线垂直
答案 D
解析 根据线面垂直的定义可知，l垂直于α内的所有直线时，l⊥α.
2．如果一条直线垂直于一个平面内的下列各种情况，能保证该直线与平面垂直的是( )
①三角形的两边；②梯形的两边；③圆的两条直径；④正六边形的两条边．
A．①③ B．② C．②④ D．①②④
答案 A
解析 由线面垂直的判定定理知，直线垂直于①③图形所在的平面．而②④图形中的两边不一定相交，故该直线与它们所在的平面不一定垂直．
3．空间四边形ABCD的四边相等，则它的两对角线AC、BD的关系是( )
A．垂直且相交
B．相交但不一定垂直
C．垂直但不相交
D．不垂直也不相交
答案 C
解析 如图，取BD中点O，
连接AO，CO，
则BD⊥AO，BD⊥CO，
∴BD⊥面AOC，
又AC⊂面AOC，
BD⊥AC.
又BD、AC异面，∴不相交．
故选C.
4.如图所示，定点A和B都在平面α内，定点P∉α，PB⊥α，C是平面α内异于A和B的动点，且PC⊥AC，则△ABC为( )
A．锐角三角形
B．直角三角形
C．钝角三角形
D．无法确定
答案 B
解析 易证AC⊥面PBC，所以AC⊥BC.
5．下列说法中错误的个数是( )
①若直线m∥平面α，直线l⊥m，则l⊥α.
②若直线l和平面α内的无数条直线垂直，则直线l与平面α必相交．
③过平面α外一点有且只有一条直线和平面α垂直．
④过直线a外一点有且只有一个平面和直线a垂直．
A．0 B．1 C．2 D．3
答案 C
解析 ①错误．若直线m∥平面α，直线l⊥m，则l与α平行、相交或l在α内、l⊥α都有可能．
②错误．若直线l和平面α内的无数条直线垂直，则直线l与平面α平行、相交或l在α内都有可能．
③正确．如图，假如l1与l2都过点P，且都与平面α垂直，设垂足分别为A与B.在平面PAB内，过一点有两条直线l1，l2与已知直线垂直，这是不可能的．所以l1和l2重合．
④正确．不论点A是否在直线a上(如图)，设过点A与直线a垂直的平面为α.如果还有一个平面β过点A与直线a垂直，且α∩β＝l，设过点A和直线a且不过l的平面为γ，且α∩γ＝b，β∩γ＝c.因为a⊥α，a⊥β，所以a⊥b，a⊥c，这样在同一平面γ内，过一点A就有两条直线b，c都与a垂直，这是不可能的．所以，过点A和直线a垂直的平面只有一个．
6.如图，三棱锥V－ABC中，VO⊥平面ABC，O∈CD，VA＝VB，AD＝BD，则下列结论中不一定成立的是( )
A．AC＝BC
B．VC⊥VD
C．AB⊥VC
D．S△VCD·AB＝S△ABC·VO
答案 B
解析 因为VA＝VB，所以VD⊥AB.
因为VO⊥平面ABC，AB⊂平面ABC，
所以VO⊥AB.
又VO∩VD＝V，VO⊂平面VCD，VD⊂平面VCD，
所以AB⊥平面VCD，
又CD⊂平面VCD，VC⊂平面VCD，
所以AB⊥VC，AB⊥CD.
又AD＝BD，所以AC＝BC(线段垂直平分线的性质)．
因为VO⊥平面ABC，所以VV－ABC＝eq \f(1,3)S△ABC·VO.
因为AB⊥平面VCD，
所以VV－ABC＝VB－VCD＋VA－VCD
＝eq \f(1,3)S△VCD·BD＋eq \f(1,3)S△VCD·AD
＝eq \f(1,3)S△VCD·(BD＋AD)
＝eq \f(1,3)S△VCD·AB，
所以eq \f(1,3)S△ABC·VO＝eq \f(1,3)S△VCD·AB，
即S△VCD·AB＝S△ABC·VO.综上知，A，C，D正确．
二、填空题
7.如图，在空间四边形ABCD中，AB，BC，CD，DA的长和两条对角线AC，BD都相等，且E为AD的中点，F为BC的中点，则直线BE和平面ADF所成的角的正弦值为________．
答案 eq \f(\r(3),3)
解析 由已知得，△BDC和△ABC是全等的等边三角形且F是BC的中点，所以BF⊥FD，BF⊥AF.
又FD∩AF＝F，故BF⊥平面AFD.
连接EF，则EF是BE所在平面AFD内的射影，∠BEF是BE与平面AFD所成的角．
设空间四边形ABCD边长为a，则在等边三角形ABD中BE＝eq \f(\r(3),2)a；在Rt△BFE中，BF＝eq \f(1,2)BC＝eq \f(1,2)a.
故sin∠BEF＝eq \f(BF,BE)＝eq \f(\r(3),3).
8.如图所示，在正方体ABCD－A1B1C1D1中，M、N分别是棱AA1和AB上的点，若∠B1MN是直角，则∠C1MN＝______.
答案 90°
解析 ∵B1C1⊥面ABB1A1，
∴B1C1⊥MN.
又∵MN⊥B1M，∴MN⊥面C1B1M，
又C1M⊂面C1B1M，
∴MN⊥C1M.∴∠C1MN＝90°.
9．在直三棱柱ABC—A1B1C1中，BC＝CC1，当底面A1B1C1满足条件________时，有AB1⊥BC1.(注：填上你认为正确的一种条件即可，不必考虑所有可能的情况)
答案 ∠A1C1B1＝90°
解析 如图所示，连接B1C，由BC＝CC1，可得BC1⊥B1C，因此，要证AB1⊥BC1，则只要证明BC1⊥平面AB1C，即只要证AC⊥BC1即可，由直三棱柱可知，只要证AC⊥BC即可．因为A1C1∥AC，B1C1∥BC，故只要证A1C1⊥B1C1即可．(或者能推出A1C1⊥B1C1的条件，如∠A1C1B1＝90°等)
10.如图，四棱锥S­ABCD底面为正方形，SD⊥底面ABCD，则下列结论中正确的有________个．
①AC⊥SB；
②AB∥平面SCD；
③SA与平面ABCD所成的角是∠SAD；
④AB与SC所成的角等于DC与SC所成的角．
答案 4
解析 ∵SD⊥平面ABCD，
∴SD⊥AC，∵ 四边形ABCD为正方形，
∴BD⊥AC，∴AC⊥平面SBD，
∴AC⊥SB，故①正确.
∵AB∥CD，AB⊄平面SDC，
∴AB∥平面SCD，故②正确．
∵SD⊥平面ABCD，
SA在底面上的射影为AD，
SA与底面ABCD所成的角为∠SAD，
③正确．
∵AB∥CD，故④也正确．
三、解答题
11.如图，正方体ABCD­A1B1C1D1的棱长为2.
(1)求证：AC⊥B1D；
(2)求三棱锥C­BDB1的体积．
(1)证明 如图，∵ABCD­A1B1C1D1为正方体，∴BB1⊥平面ABCD.
∵AC⊂平面ABCD，∴BB1⊥AC.
又∵底面ABCD为正方形，
∴AC⊥BD.
∵BB1∩BD＝B，
∴AC⊥平面BB1D.
∵B1D⊂平面BDB1，
∴AC⊥B1D.
(2)解 由(1)知AC⊥B1D，
又AC⊥BD，
∴AC⊥平面BDB1，
设AC与BD交于点O，则CO为三棱锥C­BDB1的高，
∴＝eq \f(1,3)CO·
＝eq \f(1,3)×eq \r(2)×eq \f(1,2)×2eq \r(2)×2＝eq \f(4,3)，
∴三棱锥C­BDB1的体积为eq \f(4,3).
12．如图，四棱锥P­ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD＝PD，E，F分别为CD，PB的中点．
(1)求证：EF⊥平面PAB.
(2)设AB＝eq \r(2)BC，求AC与平面AEF所成角的正弦值．
解 (1)连接BE，EP.由题意知∠PDE＝∠BCE＝90°，
因为ED＝CE，PD＝AD＝BC，
所以Rt△PDE≌Rt△BCE，
所以PE＝BE.
因为F为PB中点，
所以EF⊥PB.
因为PD⊥底面ABCD，所以PD⊥AB，
因为DA⊥AB，PD∩AD＝D，
所以AB⊥平面PAD，所以PA⊥AB.
在Rt△PAB中，因为PF＝BF，所以PF＝AF.
又因为PE＝BE＝EA，所以△EFP≌△EFA，
所以EF⊥FA.
因为PB∩AF＝F，
所以EF⊥平面PAB.
(2)不妨设BC＝1，则AB＝eq \r(2)，AC＝eq \r(3).
所以△PAB为等腰直角三角形，且PB＝2.
因为F是PB的中点，所以BF＝1，
又AF⊥PB，EF⊥PB，
AF∩EF＝F，∴PB⊥平面AEF，
连接BE交AC于G，
∵eq \f(EC,AB)＝eq \f(EG,GB)＝eq \f(1,2)，
∴在EF上取点H，使eq \f(EH,HF)＝eq \f(EG,GB)＝eq \f(1,2)，
连接AH，则GH∥BF，GH⊥面AEF，
∴∠HAG为AC与平面AEF所成的角，
∴GH＝eq \f(1,3)BF＝eq \f(1,3)，
AG＝eq \f(2,3)AC＝eq \f(2\r(3),3)，
sin∠HAG＝eq \f(GH,AG)＝eq \f(\r(3),6).
13.如图，PA⊥矩形ABCD所在的平面，M、N分别是AB、PC的中点．
(1)求证：MN∥平面PAD；
(2)若PD与平面ABCD所成的角为45°，求证：MN⊥平面PCD.
证明 (1)取PD的中点E，连接NE、AE，如图．
又∵N是PC的中点，
∴NE綊eq \f(1,2)DC.
又∵DC綊AB，AM＝eq \f(1,2)AB，
∴AM綊eq \f(1,2)CD，∴NE綊AM，
∴四边形AMNE是平行四边形，∴MN∥AE.
∵AE⊂平面PAD，MN⊄平面PAD，
∴MN∥平面PAD.
(2)∵PA⊥平面ABCD，
∴∠PDA即为PD与平面ABCD所成的角，
∴∠PDA＝45°，∴AP＝AD，∴AE⊥PD.
又∵MN∥AE，∴MN⊥PD.
∵PA⊥平面ABCD，∴PA⊥CD.
又∵CD⊥AD，∴CD⊥平面PAD.
∵AE⊂平面PAD，∴CD⊥AE.
∴CD⊥MN，又CD∩PD＝D，
∴MN⊥平面PCD.定义
如果直线l与平面α内的任意一条直线都垂直，我们就说直线l与平面α互相垂直
记法
l⊥α
有关概念
直线l叫做平面α的垂线，平面α叫做直线l的垂面，它们唯一的公共点P叫做垂足
图示
画法
画直线与平面垂直时，通常把直线画成与表示平面的平行四边形的一边垂直
文字语言
一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直
符号语言
l⊥a，l⊥b，a⊂α，b⊂α，a∩b＝P⇒l⊥α
图形语言
有关概念
对应图形
斜线
与平面α相交，但不和平面α垂直，图中直线PA
斜足
斜线和平面的交点，图中点A
射影
过斜线上斜足以外的一点向平面引垂线，过垂足和斜足的直线叫做斜线在这个平面内的射影，图中斜线PA在平面α上的射影为直线AO
直线与平面所成的角
定义：平面的一条斜线和它在平面上的射影所成的锐角，图中∠PAO
规定：一条直线垂直于平面，它们所成的角是90°；一条直线和平面平行，或在平面内，它们所成的角是0°
取值范围
设直线与平面所成的角为θ，0°≤θ≤90°