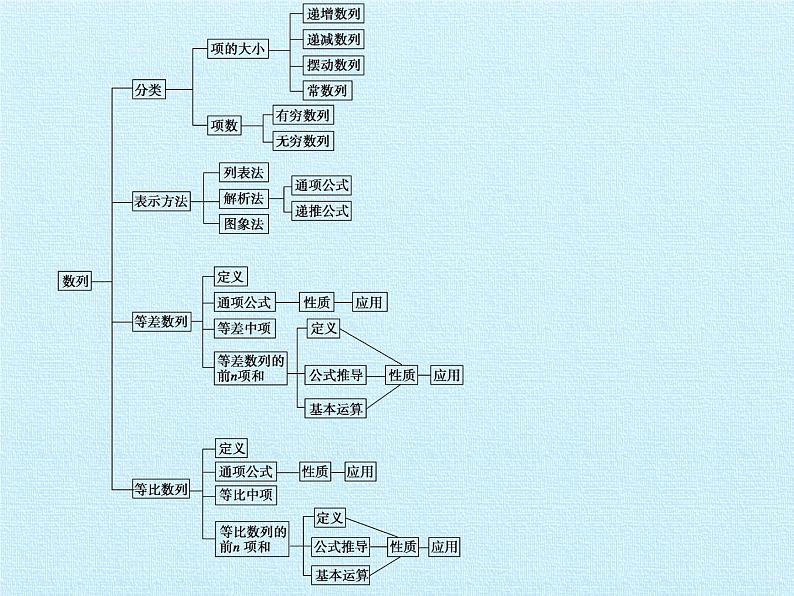
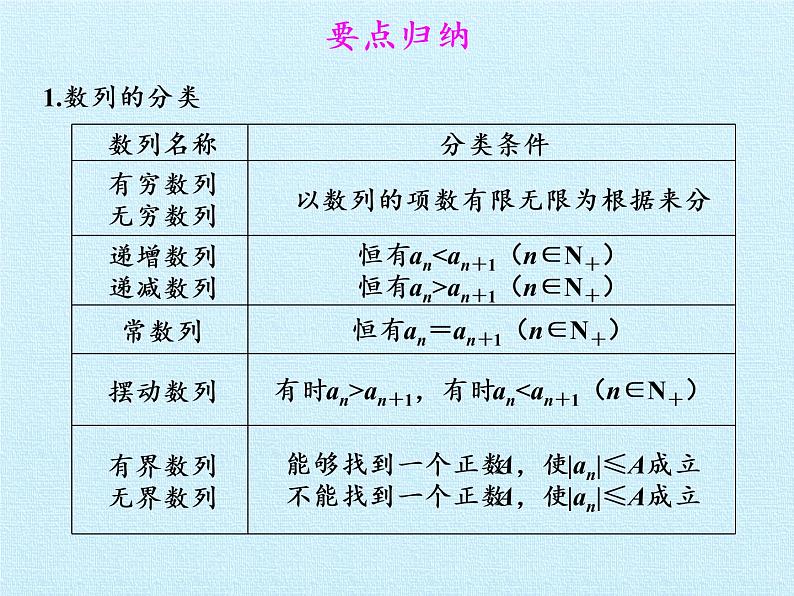
高中数学湘教版必修4第9章 数列综合与测试复习ppt课件

这是一份高中数学湘教版必修4第9章 数列综合与测试复习ppt课件，共33页。PPT课件主要包含了数列的分类，要点归纳，专题二数列求和，专题三数列应用题等内容，欢迎下载使用。

2.学习数列应注意的问题（1）在学习时，应多结合实例，通过实例去理解数列的有关概念。数列与函数密切相关，多角度比较两者之间的异同，加深对两方面内容的理解。在解题或复习时，应自觉地运用函数的思想方法去思考和解决数列问题，特别是对等差或等比数列的问题。运用函数思想方法以及利用它所得到的许多结论，不仅可以深化对数列知识的理解。而且可使这类问题的解答更为快速、合理。（2）善于对比学习。学习等差数列后，再学等比数列时，可以等差数列为模型，从等差数列研究过的问题入手，再探求出等比数列的相应问题，两相对照，
可以发现，在这两种数列的定义、一般形式、通项形式、中项及性质中，用了一些相类似的语句和公式形式，但内容却不相同，之所以有这样的区别，原因在于“差”与“比”不同。通过对比学习，加深了对两种特殊数列本质的理解，会收到事半功倍的效果。（3）要重视数学思想方法的指导作用。本章蕴含丰富的数学观点、数学思想和方法，学习时应给予充分注意，解题时多考虑与之相联系的数学思想方法。
专题一　求数列的通项公式
数列的通项公式是数列的核心之一，它如同函数中的解析式一样，有了解析式就可以研究函数的性质，而有了数列的通项公式便可以求出任何一项。所以研究数列的通项往往是解题的关键点和突破口，常用的求数列通项公式的方法有：观察法，就是观察数列特征，找出各项共同的构成规律，归纳出通项公式；
2.递推公式法，就是根据数列的递推公式，采用迭代、叠加、累乘、转化等方法产生an与a1（或Sn）的关系，得出通项公式；
方法点评　已知数列的前n项和与数列通项的关系求通项时，要注意n＝1与n≥2两种情况的分类讨论。
已知数列{an}满足a1＝1，an＝3n－1＋an－1（n≥2）。（1）解　∵a1＝1，∴a2＝3＋1＝4，a3＝32＋4＝13。（2）证明　由已知an－an－1＝3n－1，令n分别取2，3，4，…，n得a2－a1＝31，a3－a2＝32，a4－a3＝33，…an－an－1＝3n－1，
以上n－1个式子相加，得an－a1＝31＋32＋…＋3n－1方法点评　如果给出数列{an}的递推公式为an＝an－1＋f（n）型时，并且{f（n）}容易求和，这时可采用迭加法。
即an＝n（n＋1）。当n＝1时，a1＝2适合上式。故an＝n（n＋1）（n∈N*）。
方法点评　根据已知条件构造一个与an有关的新的数列，通过新数列通项公式的求解求得{an}的通项公式。新的数列往往是等差数列或是等比数列。例如形如an＝pan－1＋q（p，q为常数）的形式，往往变为an－λ＝p（an－1－λ），构成等比数列。求an－λ通项公式，再求an。
数列求和问题，是历年高考重点考查的内容之一，当然最基本的还是等差、等比数列的求和，直接利用前n项和公式来解决，我们一般称之为公式法。在此基础上，对于一些特殊的数列。我们有如下几种常用的求和方法：1.分组法：若数列{an}的通项公式形如an＝bn＋cn（也可是多项之和），而数列{ bn}，{cn}是等差或等比数列，那么，数列{an}的前n项和不就迎刃而解了吗！2.错位相减法：若数列{an}是通项公式形如an＝bn·cn，而{bn}是等差数列，{cn}是等比数列，则可采用此法。
3.并项法：一般用于摆动数列的求和问题。4.裂项相消法：把数列的通项拆成两项之差求和，正负项相消剩下首尾若干项；常见的拆项公式有：
5.倒序相加法 将一个数列倒过来排列（反序），当它与原数列相加时，若有公因式可提，并且剩余的项的和易于求得，则这样的数列可用倒序相加法求和，它是等差数列求和公式的推广。 以上是我们常用的几种求和方法，而每一种方法各有其适合的数列，观察通项公式的特点，是正确选用求和方法的关键。
等比数列{an}的前n项和为Sn，已知对任意的n∈N*，点（n，Sn）均在函数y＝bx＋r（b>0且b≠1，b，r均为常数）的图象上。（1）求r的值；解　（1）由题意，Sn＝bn＋r，当n≥2时，Sn－1＝bn－1＋r，所以an＝Sn－Sn－1＝bn－1（b－1），由于b>0且b≠1，所以当n≥2时，{an}是以b为公比的等比数列。又a1＝b＋r，a2＝b（b－1），
等差数列{an}的各项均为正数，a1＝3，前n项和为Sn，{bn}为等比数列，b1＝1，且b2S2＝64，b3S3＝960。（1）求an与bn；解　（1）设{an}的公差为d，{bn}的公比为q，则d为正数，an＝3＋（n－1）d，bn＝qn－1，
数列应用问题的学习已成为高中数学学习与研究的一个重要内容，现实生活中涉及银行利率、企业股金、产品利润、人口增长、工作效率、图形面积、曲线长度、堆积物品总数等实际问题，都需要用数列的知识加以解决。解答数列应用问题的核心是建立模型。 解数列模型的应用题，要做到以下几点： （1）认真审题，准确理解题意，认真筛选，收集和处理问题中提供的信息，善于把问题数学化。 （2）弄清题目中的主要已知事项，明确所求的结论是什么。 （3）将实际问题抽象为数列问题，将已知与所求联系起来，根据题意引出满足题意的数学关系式。 （4）在解数列应用题时，一般要经历“设—列—解—答” 四个环节。
1．与等差数列有关的实际应用题 有30根水泥电线杆，要运往1000米远的地方安装，在1000米处放一根，以后每50米放一根，一辆汽车每次只能运三根，如果用一辆汽车完成这项任务（完成任务后回到原处），那么这辆汽车的行程共为多少千米？
解　如图所示， 假定30根水泥电线杆存放在M处，则a1＝MA＝1000，a2＝MB＝1050，a3＝MC＝1100，a6＝a3＋50×3＝1250，……a30＝a3＋150×9，
由于一辆汽车每次只能装3根，故每运一次只能到a3，a6，a9，…，a30，这些地方，这样组成公差为150，首项为1100的等差数列，令汽车的行程为S，则S＝2（a3＋a6＋…＋a30）＝2（a3＋a3＋150×1＋…＋a3＋150×9）即这辆汽车的行程为35.5千米。方法点评　对于与等差数列有关的应用题，要善于发现“等差”的信息，如“每一年比上一年多（少）”“一个比一个多（少）”等，此时可化归为等差数列，明确已知a1，an，n，d，Sn中的哪几个量，求哪几个量，选择哪一个公式。
2.与等比数列有关的实际应用题 某人贷款5万元，分5年等额还清，贷款年利率为5%，按复利计算，每年需还款多少元？（精确到1元）解　设每年还款x万元。第一年偿还的x万元，还清贷款时升值为x（1＋0.05）4万元。第二年偿还的x万元，还清贷款时升值为x（1＋0.05）3万元。第三年偿还的x万元，还清贷款时升值为x（1＋0.05）2万元。第四年偿还的x万元，还清贷款时升值为x（1＋0.05）万元，第五年偿还的x万元，还清贷款时仍为x万元。
于是x（1＋0.05）4＋x（1＋0.05）3＋x（1＋0.05）2＋x（1＋0.05）＋x＝5（1＋0.05）5，方法点评　一般地，当出现下列信息时，可化归为等比数列：（1）增长率；（2）几倍；（3）几番；（4）几分之几等，此时应明确已知a1，an，Sn，q，n中的哪几个量，求哪几个量，一般是知三求二。
实际上数列也是一种特殊的函数，很多数列的问题，往往可以从函数的观点去研究，求解数列中的量如a1，an，Sn和n（或d）等常通过解方程或方程组来解。
专题四　函数与方程思想在数列中的体现