高中数学北师大版 (2019)必修 第二册4.2 平面向量及运算的坐标表示教案配套课件ppt

这是一份高中数学北师大版 (2019)必修 第二册4.2 平面向量及运算的坐标表示教案配套课件ppt，文件包含北师大版2019高中数学必修第二册242平面向量及运算的坐标表示课件共37张PPTppt、24．2平面向量及运算的坐标表示doc、课时作业20doc等3份课件配套教学资源，其中PPT共37页， 欢迎下载使用。
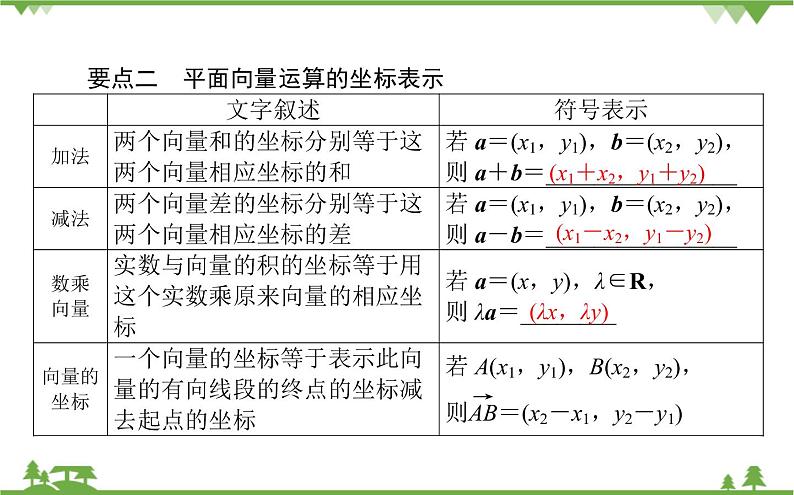
4．2　平面向量及运算的坐标表示 [教材要点]要点一　平面向量的坐标表示在平面直角坐标系中，分别取与x轴，y轴方向相同的两个单位向量i，j作为标准正交基．对于坐标平面内的任意向量a，以坐标原点O为起点作＝a(通常称为________向量)．由平面向量基本定理可知，有且仅有一对实数x，y，使＝xi＋yj.因此a＝xi＋yj，把________称为向量a在标准正交基{i，j}下的坐标，记作a＝________.　1.对平面向量坐标的几点认识(1)设 ＝x＋y(O为坐标原点)，则向量 的坐标(x，y) 就是终点A的坐标；反过来，终点A的坐标就是向量的坐标(x，y)．因此，在直角坐标系内，每一个平面向量都可以用一个有序实数对唯一表示，即以原点为起点的向量与实数对是一一对应的．(2)两向量相等的等价条件是它们对应的坐标相等．(3)要把点的坐标与向量的坐标区别开来，相等的向量的坐标是相同的，但起点和终点的坐标却可以不同．2．符号(x，y)的意义符号(x，y)在直角坐标系中有两重意义，它既可以表示一个固定的点，又可以表示一个向量，为了加以区分，在叙述中，就常说点(x，y)或向量(x，y)．要点二　平面向量运算的坐标表示  文字叙述符号表示加法两个向量和的坐标分别等于这两个向量相应坐标的和若a＝(x1，y1)，b＝(x2，y2)，则a＋b＝________________减法两个向量差的坐标分别等于这两个向量相应坐标的差若a＝(x1，y1)，b＝(x2，y2)，则a－b＝________________数乘向量实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标若a＝(x，y)，λ∈R，则λa＝________向量的坐标一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标若A(x1，y1)，B(x2，y2)，则＝(x2－x1，y2－y1)　(1)向量的坐标与表示向量的有向线段的起点、终点的具体位置没有关系，只与其相对位置有关系，即两向量的坐标相同时，两个向量相等，但它们的起点和终点的坐标却不一定相同．例如，若A(3,5)，B(6,8)，C(－5,3)，D(－2,6)，则 ＝(3,3)， ＝(3,3)，显然 ＝，但A，B，C，D各点的坐标都不相同．(2)运算时，注意向量的起点与终点的顺序不要颠倒．要点三　中点坐标公式设点A(x1，y1)，B(x2，y2)，M是线段AB的中点，则要点四　平面向量平行的坐标表示a＝(x1，y1)，b＝(x2，y2)向量a，b(b≠0)共线的充要条件是____________．   　已知＝(x1，y1)，＝(x2，y2)，(1)当≠0时，＝λ.这是几何运算，体现了向量与的长度及方向之间的关系．(2)x1y2－x2y1＝0.这是代数运算，用它解决向量共线问题的优点在于不需要引入参数“λ”，从而减少未知数个数，而且使问题的解决具有代数化的特点、程序化的特征．(3)当x2y2≠0时，＝，即两向量的对应坐标成比例．通过这种形式较易记忆向量共线的坐标表示，而且不易出现搭配错误．[基础自测]1．判断正误(正确的画“√”，错误的画“×”)(1)两个向量的终点不同，则这两个向量的坐标一定不同．(　　)(2)向量的坐标就是向量终点的坐标．(　　)(3)在平面直角坐标系中，两个相等向量的坐标相同．(　　)(4)两向量差的坐标与两向量的顺序无关．(　　)(5)点的坐标与向量的坐标相同．(　　)(6)若a＝(x1，y1)，b＝(x2，y2)，a∥b，则x1y2＝x2y1.(　　)2．已知M(2,3)，N(3,1)，则的坐标是(　　)  A．(2，－1)  B．(－1,2)C．(－2,1)  D．(1，－2)3．已知a＝(－6,2)，b＝(m，－3)，且a∥b，则m＝(　　)  A．－9  B．9C．3  D．－34．已知A(1,2)，B(4,5)．若＝2，则点P的坐标为________.题型一　平面向量的坐标表示——师生共研例1　(1)设i＝(1,0)，j＝(0,1)，a＝3i＋4j，b＝－i＋j，求a＋b与a－b的坐标．(2)如图，在边长为1的正方形ABCD中，AB与x轴正半轴成30 °角．求点B，D的坐标和，的坐标．                   方法归纳在向量的坐标表示中，一定要分清表示向量的有向线段的起点与终点的坐标，同时注意区分点的坐标与向量的坐标写法的不同． 跟踪训练1　(1)已知e1，e2是平面内两个相互垂直的单位向量，且a＝4e1－3e2，则向量a的坐标为(　　)  A．(4e1,3e2)  B．(4e1，－3e2)C．(4,3)  D．(4，－3)(2)已知O是坐标原点，点A在第二象限，||＝6，∠xOA＝150°，向量的坐标为________．题型二　平面向量的坐标运算——自主完成已知A(－2,4)，B(3，－1)，C(－3，－4)．设＝a，＝b，＝c，且＝3c，＝－2b.(1)求3a＋b－3c；(2)求满足a＝mb＋nc的实数m，n；(3)求点M，N的坐标及向量的坐标．       
方法归纳1．向量的坐标运算主要是利用加、减、数乘运算法则进行的，若已知有向线段两端点的坐标，则应先求出向量的坐标，然后再进行向量的坐标运算，另外，解题过程中要注意方程思想的运用．2．利用向量的坐标运算解题，主要根据相等的向量坐标相同这一原则，通过列方程(组)进行求解．  题型三　平面向量共线的坐标表示——微点探究微点1　向量共线的判定与证明例2　已知A，B，C三点的坐标分别为(－1,0)，(3，－1)，(1,2)，＝，＝，求证：∥.            方法归纳向量共线的判定方法(1)利用向量共线定理，由a＝λb(b≠0)推出a∥b.(2)利用向量共线的坐标表达式x1y2－x2y1＝0(a＝(x1，y1)，b＝(x2，y2))直接判断a与b是否平行． 微点2　利用向量共线的坐标表示求参数例3　已知向量a＝(1,2)，b＝(λ，1)．若(a＋2b)∥(2a－2b)，则λ的值为(　　)A.  B.C．1  D．2 方法归纳根据向量共线的条件求参数问题的两种思路(1)利用向量共线定理，由a＝λb(b≠0)列方程组求解．(2)利用向量共线的坐标表达式x1y2－x2y1＝0求解． 微点3　三点共线问题例4　已知向量＝i－2j，＝2i＋μj，其中i，j分别是x轴、y轴正方向上的单位向量，试确定实数μ的值，使A，B，C三点共线．      方法归纳利用向量解决三点共线问题的一般思路：(1)利用三点构造出两个向量，求出唯一确定的实数λ；(2)利用向量运算的坐标表示得出两向量共线，再结合两向量过同一点，可得两向量所在的直线必重合，即三点共线．  跟踪训练2　(1)已知A(2,1)，B(0,4)，C(1,3)，D(5，－3)，判断与是否共线，如果共线，它们的方向相同还是相反？ (2)已知向量a＝(1,1)，b＝(－1,3)，c＝(2,1)，且(a－λb)∥c，则λ＝(　　)A．3  B．－3C.  D．－(3)已知A(1，－3)，B，且A，B，C三点共线，则点C的坐标可以是(　　)A．(－9,1)  B．(9，－1)C．(9,1)  D．(－9，－1)易错辨析　误把向量的坐标当作点的坐标运算致误例5　已知点A(2,3)，B(5,4)，C(7,10)，若＝＋λ(λ∈R)，试求当点P在第三象限时λ的取值范围．解析：由已知得＝＋λ＝(5－2,4－3)＋λ(7－2,10－3)＝(3,1)＋λ(5,7)＝(3＋5λ，1＋7λ)，设点P(x，y)，则＝(x－2，y－3)．于是(x－2，y－3)＝(3＋5λ，1＋7λ)，即又点P在第三象限，所以解得λ<－1.故λ的取值范围为(－∞，－1)．易错警示易错原因纠错心得误把向量的坐标当作点P的坐标运算致错，得到错误答案.向量的坐标反映的是向量的长度和向量的方向，与终点坐标无关，只有当向量的起点是坐标原点时，向量的坐标与终点的坐标才是一致的.4．2　平面向量及运算的坐标表示新知初探·课前预习[教材要点]要点一位置　(x，y)　(x，y)要点二(x1＋x2，y1＋y2)　(x1－x2，y1－y2)　(λx，λy)要点三　要点四x1y2－x2y1＝0[基础自测]1．(1)×　(2)×　(3)√　(4)×　(5)×　(6)√2．解析：＝(2－3,3－1)＝(－1,2)．答案：B3．解析：因为a＝(－6,2)，b＝(m，－3)，若a∥b，则－6×(－3)－2m＝0，解得m＝9.答案：B4．解析：设P(x，y)，所以＝(x－1，y－2)，＝(4－x,5－y)，又＝2，所以(x－1，y－2)＝2(4－x,5－y)，即解得答案：(3,4)题型探究·课堂解透题型一例1　解析：(1)∵a＝3i＋4j，b＝－i＋j，∴a＋b＝(3i＋4j)＋(－i＋j)＝2i＋5j，a－b＝(3i＋4j)－(－i＋j)＝4i＋3j.又∵i＝(1,0)，j＝(0,1)，∴a＋b与a－b的坐标分别是(2,5)与(4,3)．(2)由题意知，点B，D分别是30°，120°角的终边与单位圆的交点．设B(x1，y1)，D(x2，y2)．由三角函数的定义，得x1＝cos 30°＝，y1＝sin 30°＝，x2＝cos 120°＝－，y2＝sin 120°＝，∴B，D.∴＝，＝.跟踪训练1　解析：(1)∵e1，e2是互相垂直的单位向量，且a＝4e1－3e2，∴a＝(4，－3)．(2)设点A(x，y)则x＝||cos 150°＝6cos 150°＝－3，y＝||sin 150°＝6sin 150°＝3即A(－3，3)，∴＝(－3，3)．答案：(1)D　(2)(－3，3)题型二解析：由已知得a＝(5，－5)，b＝(－6，－3)，c＝(1,8)．(1)3a＋b－3c＝3(5，－5)＋(－6，－3)－3(1,8)＝(15－6－3，－15－3－24)＝(6，－42)．(2)∵mb＋nc＝(－6m＋n，－3m＋8n)，∴解得∴实数m的值为－1，n的值为－1.(3)设O为坐标原点．∵＝－＝3c，∴＝3c＋＝(3,24)＋(－3，－4)＝(0,20)，∴M(0,20)．又∵＝－＝－2b，∴＝－2b＋＝(12,6)＋(－3，－4)＝(9,2)，∴N(9,2)．∴＝(9，－18)．题型三例2　解析：设E(x1，y1)，F(x2，y2)．由题意知＝(2,2)，＝(－2,3)，＝(4，－1)，∴＝＝，＝＝，∴(x1，y1)－(－1,0)＝，(x2，y2)－(3，－1)＝.∴(x1，y1)＝，(x2，y2)＝.∴＝(x2，y2)－(x1，y1)＝.∵4×－(－1)×＝0，∴∥.例3　解析：方法一：由题意得a＋2b＝(1,2)＋2(λ，1)＝(1＋2λ，4)，2a－2b＝2(1,2)－2(λ，1)＝(2－2λ，2)．∵(a＋2b)∥(2a－2b)，∴2(1＋2λ)－4(2－2λ)＝0，解得λ＝.方法二：假设a，b不共线，则由(a＋2b)∥(2a－2b)可得a＋2b＝μ(2a－2b)，∴方程组显然无解，∴a＋2b与2a－2b不共线，这与(a＋2b)∥(2a－2b)矛盾，∴假设不成立，∴a，b共线，∴＝2，解得λ＝.答案：A例4　解析：方法一：∵A，B，C三点共线，即，共线，∴存在实数λ，使＝λ，即i－2j＝λ(2i＋μj)．可得解得故当μ＝－4时，A，B，C三点共线．方法二：依题意得i＝(1,0)，j＝(0,1)，∴＝(1,0)－2(0,1)＝(1，－2)，＝2(1,0)＋μ(0,1)＝(2，μ)．∵A，B，C三点共线，即，共线，∴1×μ－2×(－2)＝0，解得μ＝－4.故当μ＝－4时，A，B，C三点共线．跟踪训练2　解析：(1)∵＝(0,4)－(2,1)＝(－2,3)，＝(5，－3)－(1,3)＝(4，－6)，(－2)×(－6)－3×4＝0，∴，共线．又∵CD＝－2，∴，方向相反．综上，与 共线且方向相反．解析：(2)a－λb＝(1＋λ，1－3λ)．∵(a－λb)∥c，∴2(1－3λ)＝1＋λ，解得λ＝.答案：C 解析：(3)设点C的坐标是(x，y)，因为A，B，C三点共线，所以∥.因为＝－(1，－3)＝，＝(x，y)－(1，－3)＝(x－1，y＋3)，所以7(y＋3)－(x－1)＝0，整理得x－2y＝7，经检验可知点(9,1)符合要求，故选C.答案： C