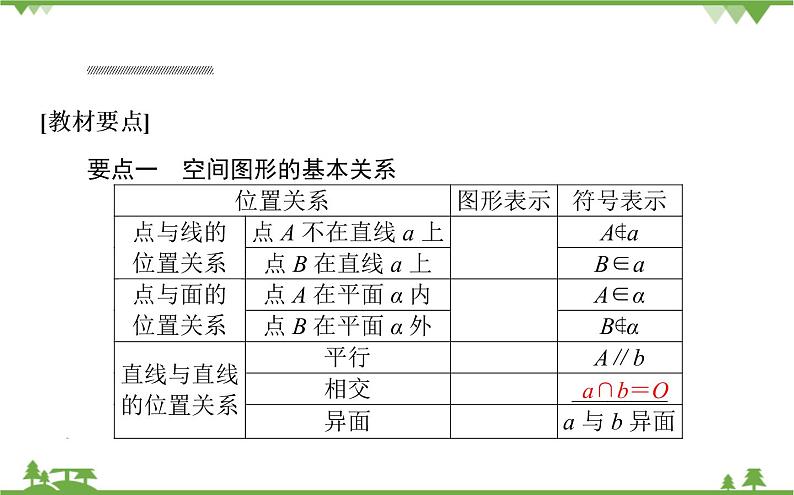
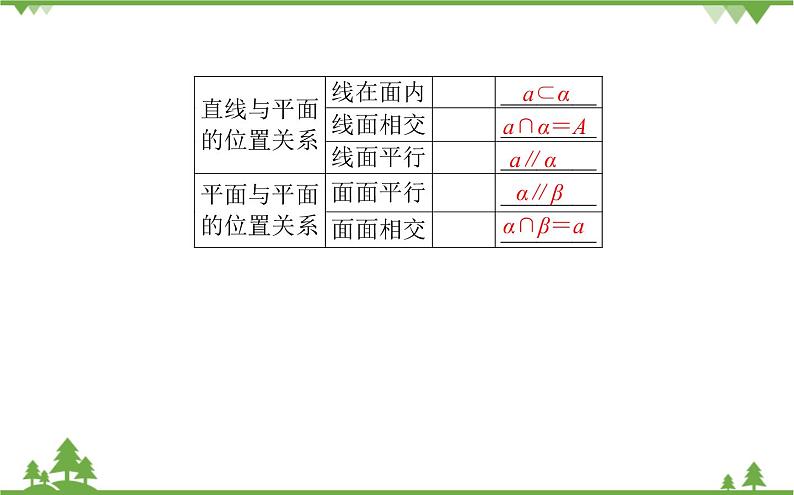
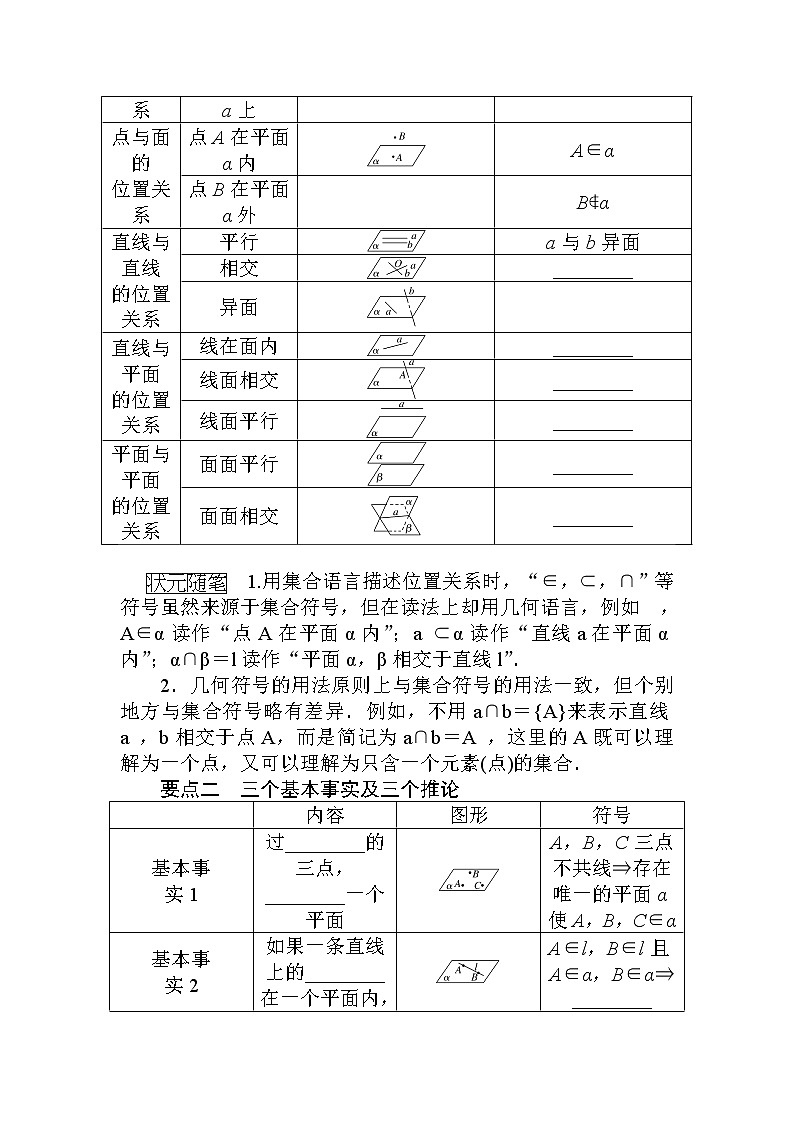
高中数学北师大版 (2019)必修 第二册3.1 空间图形基本位置关系的认识课前预习课件ppt

课时作业41　空间图形基本位置关系的认识　空间图形的基本事实1、2、3

[练基础]

1．给出下面四个命题：

①三个不同的点确定一个平面；

②一条直线和一个点确定一个平面；

③空间两两相交的三条直线确定一个平面；

④两条平行直线确定一个平面．

其中正确的命题是(　　)

A．①  B．②

C．③  D．④

2．空间中四点可确定的平面有(　　)

A．1个  B．3个

C．4个  D．1个或4个或无数个

3．给出以下四个命题：

①不共面的四点中，其中任意三点不共线；

②若点A，B，C，D共面，点A，B，C，E共面，则点A，B，C，D，E共面；

③若直线a，b共面，直线a，c共面，则直线b，c共面；

④依次首尾相接的四条线段必共面．

其中正确命题的个数是(　　)

A．0  B．1

C．2  D．3

4．设平面α与平面β相交于直线l，直线a⊂α，直线b⊂β，a∩b＝M，则点M与l的位置关系为________．

5．把下列符号叙述所对应的图形的序号填在题后的横线上：

(1)A∉α，a⊂α：________.

(2)α∩β＝a，P∉α，且P∉β：________.

(3)a⊄α，a∩α＝A：________.

(4)α∩β＝a，α∩γ＝c，β∩γ＝b，a∩b∩c＝O：________.

6.

如图所示，已知直线a∥b∥c，l∩a＝A，l∩b＝B，l∩c＝C.求证：直线a，b，c和l共面．

[提能力]

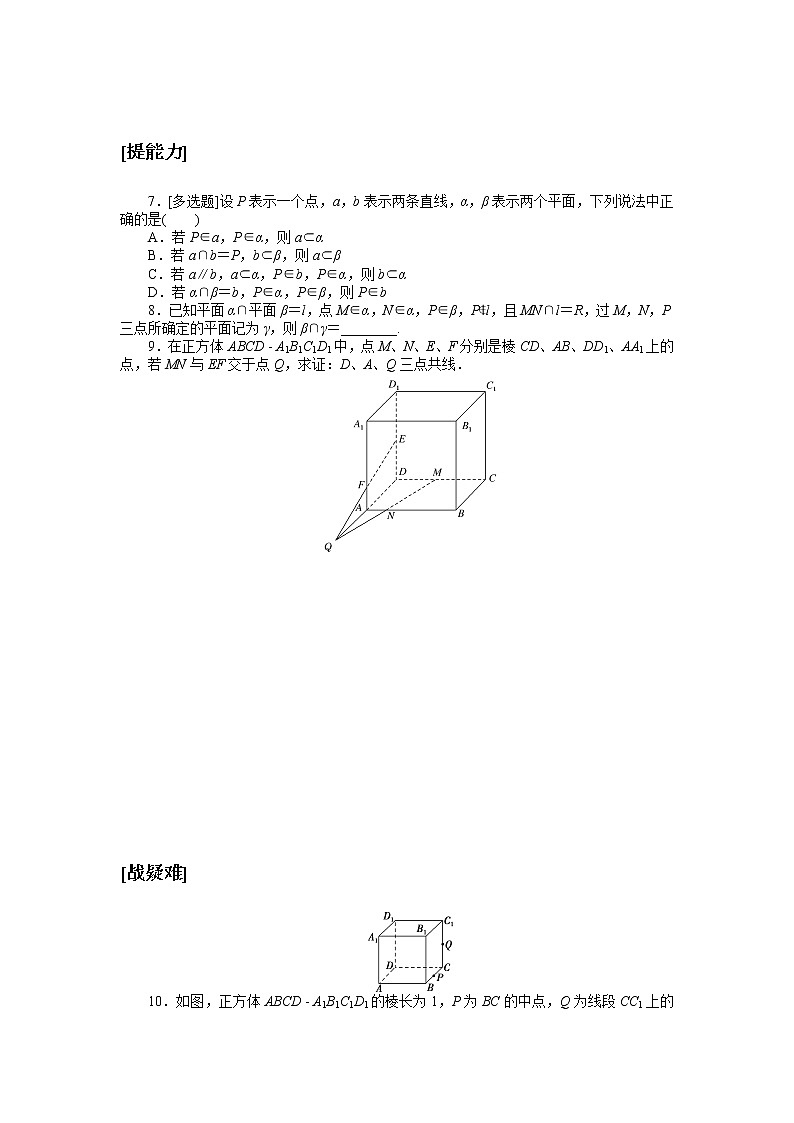
7．[多选题]设P表示一个点，a，b表示两条直线，α，β表示两个平面，下列说法中正确的是(　　)

A．若P∈a，P∈α，则a⊂α

B．若a∩b＝P，b⊂β，则a⊂β

C．若a∥b，a⊂α，P∈b，P∈α，则b⊂α

D．若α∩β＝b，P∈α，P∈β，则P∈b

8．已知平面α∩平面β＝l，点M∈α，N∈α，P∈β，P∉l，且MN∩l＝R，过M，N，P三点所确定的平面记为γ，则β∩γ＝________.

9．在正方体ABCD ­ A1B1C1D1中，点M、N、E、F分别是棱CD、AB、DD1、AA1上的点，若MN与EF交于点Q，求证：D、A、Q三点共线．

[战疑难]

10．如图，正方体ABCD ­ A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S，则下列命题中正确的是______(写出所有正确命题的编号)．

①当0＜CQ＜时，S为四边形；

②当CQ＝时，S为等腰梯形；

③当CQ＝时，S与C1D1的交点R满足C1R＝；

④当＜CQ＜1时，S为六边形；

⑤当CQ＝1时，S的面积为.

课时作业41　空间图形基本位置关系的认识　

空间图形的基本事实1、2、31.解析：对于①，三个不共线的点确定一个平面，故错；对于②，一条直线和直线外一个点确定一个平面，故错；对于③，空间两两相交的三条直线，且不能交于同一点，确定一个平面，故错；对于④，两条平行直线确定一个平面，正确．

答案：D

2．解析：当四个点共线时，确定无数个平面；当四个点不共线时，若四点共面，可确定1个平面，若四点不共面，可确定4个平面，∴空间中四点可确定的平面有1个或4个或无数个．

答案：D

3.

解析：①假设其中有三点共线，则该直线和直线外的另一点确定一个平面，这与四点不共面矛盾，故其中任意三点不共线，所以①正确；②如图，两个相交平面有三个公共点A，B，C，但A，B，C，D，E不共面；③显然不正确；④不正确，因为此时所得的四边形的四条边可以不在一个平面上，如空间四边形．

答案：B

4．解析：因为a∩b＝M，a⊂α，b⊂β，所以M∈α，M∈β.又平面α与平面β相交于直线l，所以点M在直线l上，即M∈l.

答案：M∈l

5．答案：(1)③　(2)④　(3)①　(4)②

6．证明：∵a∥b，∴a，b确定一个平面α.

∵A∈a，B∈b，∴A∈α，B∈α.

则a，b，l都在平面α内，即b在a，l确定的平面内．

同理可证c在a，l确定的平面内．

∵过a与l只能确定一个平面，

∴a，b，c，l共面于a，l确定的平面．

7．解析：当a∩α＝P时，P∈a，P∈α，但a⊄α，故A错；当a∩β＝P时，B错；∵a∥b，P∈b，∴P∉a，∴由直线a与点P确定唯一平面α，又a∥b，由a与b确定唯一平面β，但β经过直线a与点P，∴β与α重合，∴b⊂α，故C正确；两个平面的公共点必在其交线上，故D正确，故选CD.

答案：CD

8．解析：

如图所示，MN⊂γ，R∈MN，

∴R∈γ.

又R∈l，∴R∈β.

∵P∈γ，P∈β，

∴β∩γ＝PR.

答案：PR

9．解析：∵MN∩EF＝Q，∴Q∈直线MN，Q∈直线EF，

∵M∈直线CD，N∈直线AB，CD⊂平面ABCD，AB⊂平面ABCD，

∴M、N∈平面ABCD，∴MN⊂平面ABCD，

∴Q∈平面ABCD.

同理，EF⊂平面ADD1A1，∴Q∈平面ADD1A1，

又∵平面ABCD∩平面ADD1A1＝AD，

∴Q∈直线AD，即D，A，Q三点共线．

10．解析：①当0＜CQ＜时，如图(1)．

在平面AA1D1D内，作AE∥PQ.

显然点E在棱DD1上，连接EQ，

则S是四边形APQE.

②当CQ＝时，如图(2)．

显然PQ∥BC1∥AD1，连接D1Q，

则S是等腰梯形．

③当CQ＝时，如图(3)．

作BF∥PQ，交线段CC1的延长线于点F，则C1F＝.

作AE∥BF，交线段DD1的延长线于点E，则D1E＝，AE∥PQ.

连接EQ交C1D1于点R，易知Rt△RC1Q∽Rt△RD1E，

则C1QD1E＝C1RD1R＝12，可得C1R＝.

④当＜CQ＜1时，如图(4)．

同③可作BF∥PQ，交线段CC1的延长线于点F.

作AE∥BF，交线段DD1的延长线于点E.

连接EQ交C1D1于点R.

连接RM(点M为AE与A1D1的交点)，

显然S为五边形APQRM.

⑤当CQ＝1时，如图(5)．

同③可作AE∥PQ交线段DD1的延长线于点E，交A1D1于点M，显然点M为线段A1D1的中点，所以S为菱形APQM，其面积为MP·AQ＝××＝.

答案：①②③⑤