

北师大版九年级上册2 平行线分线段成比例学案设计
展开1.探索并掌握基本事实“平行线分线段成比例”及其推论.
2.会熟练运用平行线分线段成比例定理及其推论计算线段的长度。
3.体会特殊到一般的归纳推理的思想和方法.
温故知新
若线段a,b,c,d是成比例线段,则可列比例式为 ;
若a=3㎝,b=4㎝,c=6㎝,则d=___________㎝.
3.如果把ad=bc写成线段的比例式,那么正确的比例式是 你能写出几个?他们之间什么关系?
三、自主探究:阅读课本p82—85
探究(一)如图,小方格的边长均为1,直线∥∥,
分别交直线m,n于点
1.利用勾股定理计算:
; ; ; ; ; .
2.计算: , ; , ; , .
由上可知,你有什么发现?请把你的发现写出来.
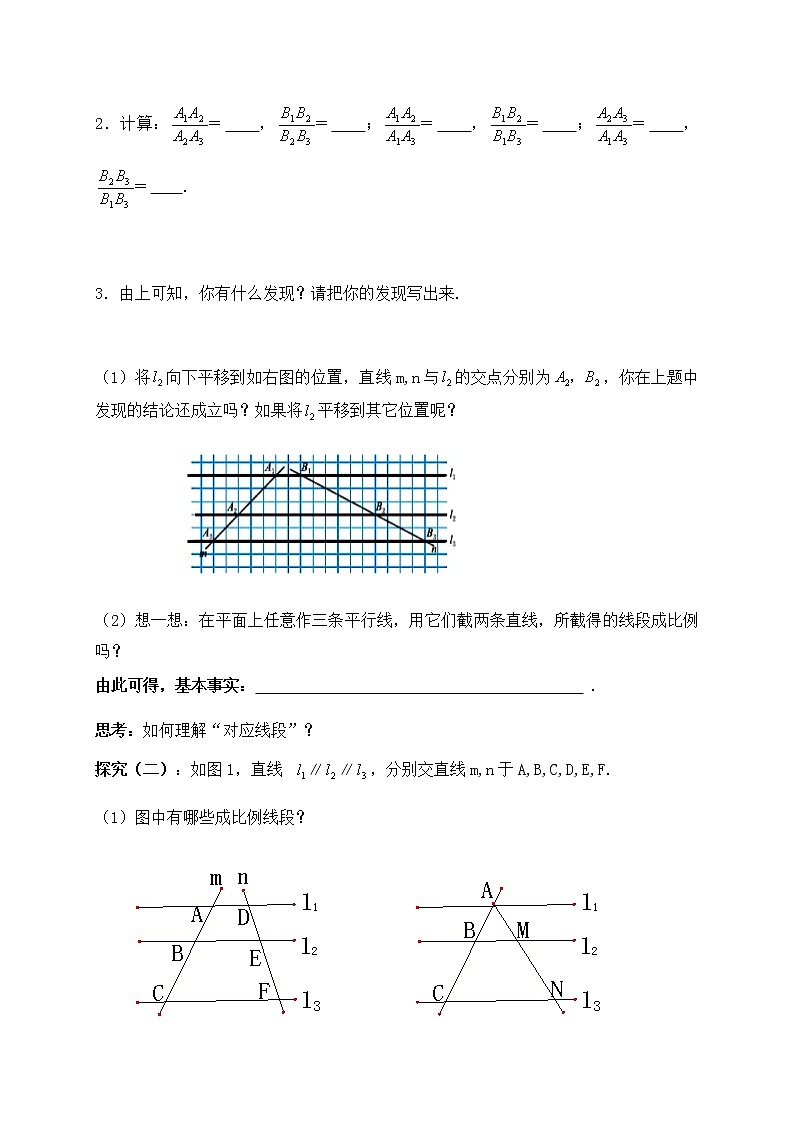
(1)将向下平移到如右图的位置,直线m,n与的交点分别为,你在上题中发现的结论还成立吗?如果将平移到其它位置呢?
(2)想一想:在平面上任意作三条平行线,用它们截两条直线,所截得的线段成比例吗?
由此可得,基本事实: .
思考:如何理解“对应线段”?
探究(二):如图1,直线∥∥,分别交直线m,n于A,B,C,D,E,F.
(1)图中有哪些成比例线段?
(1) (2)
(2)如图2,平移直线n,使点D与点A重合,与,分别交于点M,N,图中有哪些成比例线段?
(3)由此可得,推论: .
几何语言表示为 .
例1:如图,在△ABC中,E, F分别是AB和AC上的点,且 EF∥BC.
(1)如果AE = 7, EB=5,FC = 4,那么AF的长是多少?
(2)如果AB = 10, AE=6,AF = 5,那么FC的长是多少?
例2:如图,在△ABC中,D,E分别是AB和BC上的点,且DE//AC,
ABBE=ACEC,ABAC=53,求ABBD.
四、随堂练习 :
1.已知两条直线被三条平行线所截,截得线段的长度如图所示,则x= .
2.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若AD∶AB=3∶4,AE=6,则AC等于( )
A. 3 B. 4 .C. 6 D.8
(第1题) (第2 题) (第3题)
3.如图所示,直线∥∥,下列比例式中错误的是( )
五:本课小结:
本节课知识点:
你还有什么收获或困惑?
六:当堂检测:
1.如图,已知 DE∥BC, AB = 5, AC = 7,AD= 2,求AE的长.
2.如图,已知直线∥∥,DE = 6, EF = 7,AB=5,求AC的长.
3.如图,在△ABC中,D,E,F分别是AB,AC,BC上的点,且DE//BC,EF//AB,AD:DB=2:3,BC=20cm,求BF的长度。
课堂作业:P84: 习题4.3 。1、2、
答案:
四、随堂练习 :
1.
2.D.
3. B.
六:当堂检测:
1.
2.
3.8
初中数学北师大版九年级上册第四章 图形的相似2 平行线分线段成比例学案设计: 这是一份初中数学北师大版九年级上册第四章 图形的相似2 平行线分线段成比例学案设计,共7页。学案主要包含了问题引入,基础训练,例题展示,课堂检测等内容,欢迎下载使用。
北师大版九年级上册2 平行线分线段成比例导学案: 这是一份北师大版九年级上册2 平行线分线段成比例导学案,共3页。学案主要包含了学习准备,学习目标,学习过程,作业布置,学习小结等内容,欢迎下载使用。
初中数学北师大版九年级上册2 平行线分线段成比例导学案: 这是一份初中数学北师大版九年级上册2 平行线分线段成比例导学案,共5页。学案主要包含了学习目标,学习过程,学习反思等内容,欢迎下载使用。













