数学九年级上册2 矩形的性质与判定导学案

这是一份数学九年级上册2 矩形的性质与判定导学案，共8页。学案主要包含了学习目标，温故知新，自主探究，随堂练习 ，小结等内容，欢迎下载使用。
一、学习目标
1、掌握矩形的性质定理及判定方法，
2、能用矩形的性质判定解决相关的数学问题。
二、温故知新
1、矩形的定义： 的平行四边形叫做矩形。
2、矩形的性质：⑴矩形具有平行四边形的的一切性质； ⑵矩形的四个角都是 ；⑶矩形的对角线 。
3、矩形的判定
⑴定义： 的平行四边形叫做矩形。
⑵定理： 的平行四边形叫做矩形；
⑶定理：三个角是 的四边形叫做矩 .
4.如图1，矩形ABCD的两条对角线相交于点O，已知∠AOD= 120°，AB=2.5cm，则
∠DAO= ,AC= cm，_______。

5.如图2，四边形ABCD是平行四边形，添加一个条件 ，可使它成为矩形。
三、自主探究：阅读课本p16—18
探究（一）、（以下几例看懂会讲）
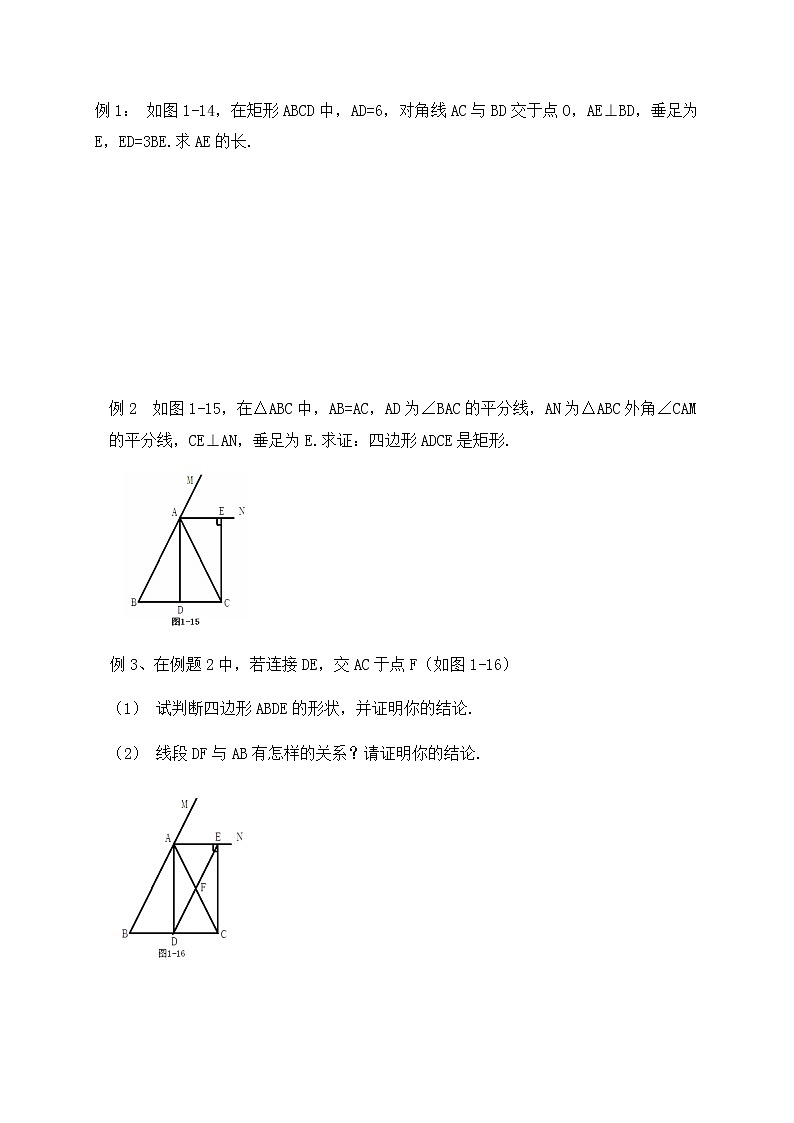
例1： 如图1-14，在矩形ABCD中，AD=6，对角线AC与BD交于点O，AE⊥BD，垂足为E，ED=3BE.求AE的长.
例2 如图1-15，在△ABC中，AB=AC，AD为∠BAC的平分线，AN为△ABC外角∠CAM的平分线，CE⊥AN，垂足为E.求证：四边形ADCE是矩形.
例3、在例题2中，若连接DE，交AC于点F（如图1-16）
试判断四边形ABDE的形状，并证明你的结论.
线段DF与AB有怎样的关系？请证明你的结论.
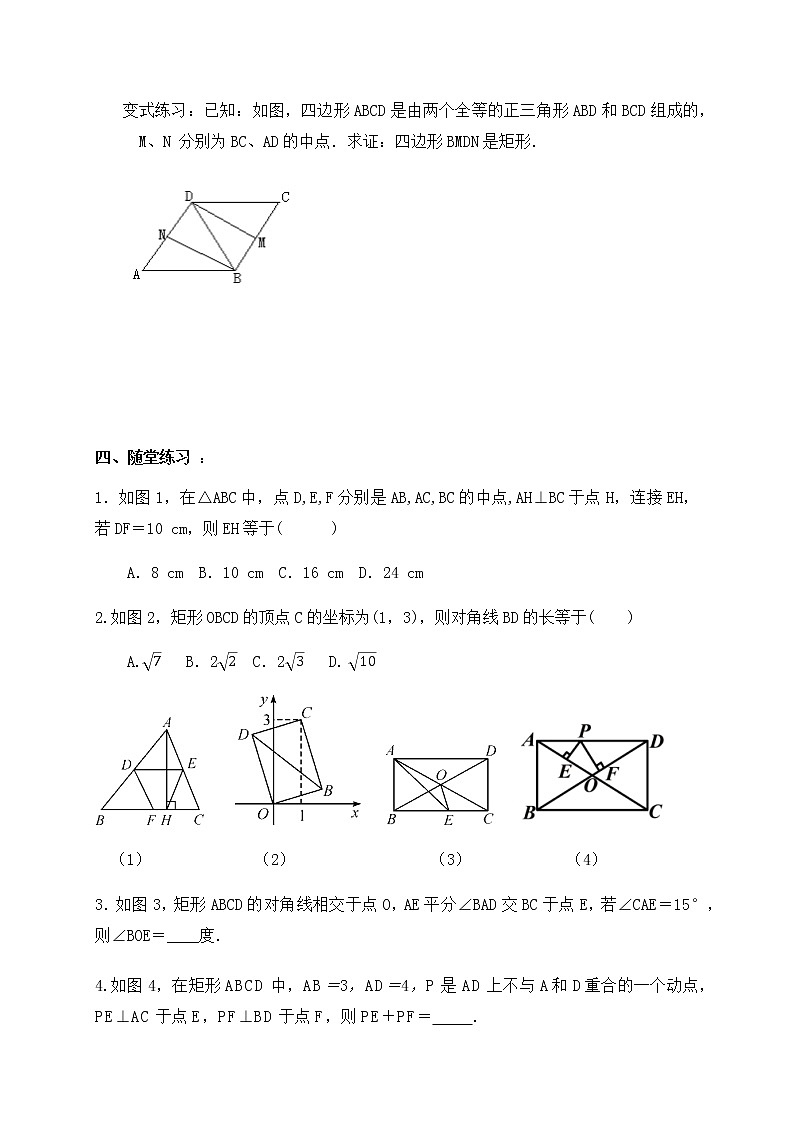
变式练习：已知：如图，四边形ABCD是由两个全等的正三角形ABD和BCD组成的，M、N分别为BC、AD的中点．求证：四边形BMDN是矩形．
四、随堂练习 ：
1．如图1，在△ABC中，点D,E,F分别是AB,AC,BC的中点,AH⊥BC于点H，连接EH，若DF＝10 cm，则EH等于( )
A．8 cm B．10 cm C．16 cm D．24 cm
2.如图2，矩形OBCD的顶点C的坐标为(1，3)，则对角线BD的长等于( )
A.7 B．22 C．23 D. 10

（1） （2） （3） （4）
3．如图3，矩形ABCD的对角线相交于点O，AE平分∠BAD交BC于点E，若∠CAE＝15°，则∠BOE＝____度．
4.如图4，在矩形ABCD中，AB＝3，AD＝4，P是AD上不与A和D重合的一个动点，PE⊥AC于点E，PF⊥BD于点F，则PE＋PF＝ .
五、小结：本课知识：
说说你的收获
说说你的困惑。
说说你的方法。
六：当堂检测：
1．如图1，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1，S2，则S1，S2的大小关系是( )
A．S1>S2 B．S1＝S2 C．S1