2021年广东省初中学业水平考试冲刺9练习题

这是一份2021年广东省初中学业水平考试冲刺9练习题，共31页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
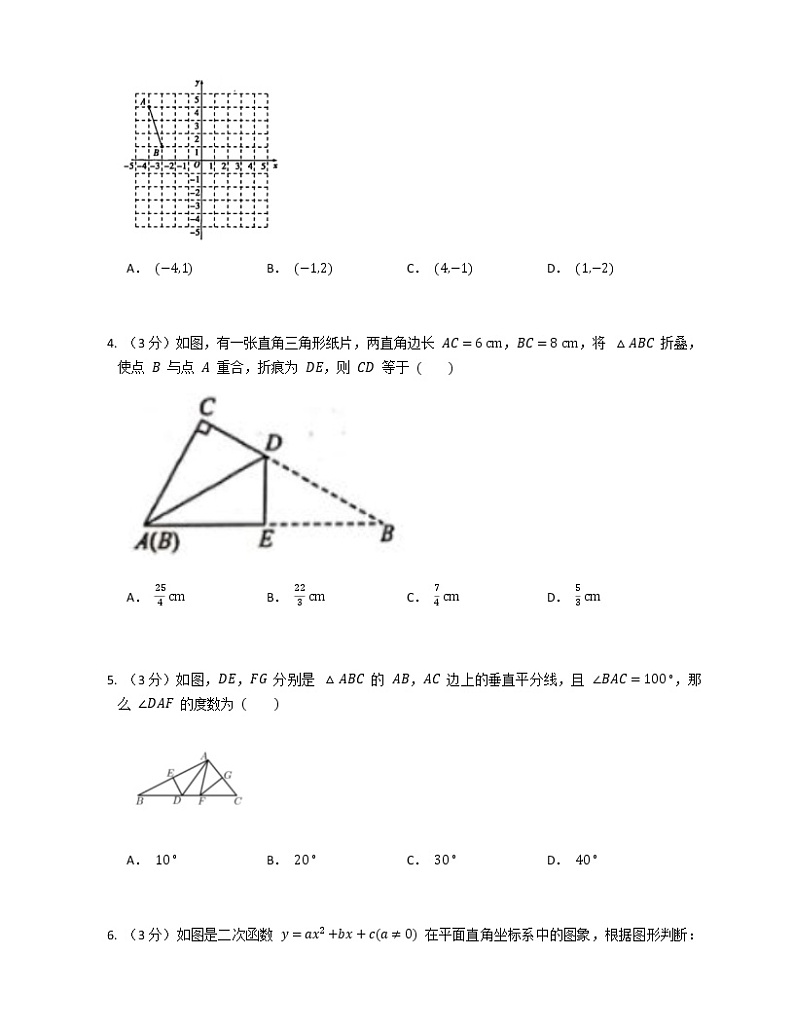
2021年广东省初中学业水平考试冲刺9一、选择题（30分）（3分）如图，在 中，，，则 的度数为  A．  B．  C．  D．  （3分）如图， 为正方形 边 上一动点（不与 重合），，将 绕点 逆时针旋转 得到 ，再将 沿直线 折叠得到 ．下列结论：①连接 ，则 ；②连接 ，当 ，， 三点共线时，；③连接 ，，，若 是等腰三角形，则 ；④连接 ，设 ， 交于点 ，若 平分 ，则 是 的中点，且 ；其中正确的个数有 个． A．  B．  C．  D．  （3分）如图，将线段 先向右平移 个单位，再将所得线段绕原点按顺时针方向旋转 ，得到线段 ，则点 的对应点 的坐标是  A．  B．  C．  D．  （3分）如图，有一张直角三角形纸片，两直角边长 ，，将 折叠，使点 与点 重合，折痕为 ，则 等于  A．  B．  C．  D．  （3分）如图，， 分别是 的 ， 边上的垂直平分线，且 ，那么 的度数为  A．  B．  C．  D．  （3分）如图是二次函数 在平面直角坐标系中的图象，根据图形判断：① ；② ；③ ；④ 中正确的是     A．①② B．①③ C．③④ D．②④ （3分）如图，在正方形 中，对角线 ， 相交于点 ，点 在 边上，且 ，连接 交 于点 ，过点 作 于点 ，连接 并延长，交 于点 ，过点 作 交 于点 ，．现给出下列结论：① ；② ；③ ；④ ；其中正确的结论有  A．①②③ B．②③④ C．①②④ D．①③④ （3分）如图，动点 在平面直角坐标系中按图中箭头所示方向运动，第 次从原点运动到点 ，第 次接着运动到点 ，第 次接着运动到点 ， 按这样的运动规律，经过第 次运动后，动点 的坐标是  A．  B．  C．  D．  （3分）已知点，关于轴的对称点'在反比例函数的图象上，则实数的值为　　 A．3 B． C． D． （3分）某地一周前四天每天的最高气温与最低气温如表，则这四天中温差最大的是　　\(\begin{array}{|c|c|c|c|c|}\hline 星期&一&二&三&四\\\hline 最高气温&10^{\circ} C&12^{\circ} C&11^{\circ} C&9^{\circ} C\\\hline 最低气温&3^{\circ} C&0^{\circ} C&-2^{\circ} C&-3^{\circ} C\\\hline\end{array}\) A．星期一 B．星期二 C．星期三 D．星期四 二、填空题（28分）（4分）如果 的小数部分为 ， 的整数部分为 ，小数部分为 ，则 的值为    （精确到 ）． （4分）如图（）所示，在 中，，，，将 沿着 翻折得到 ，如图（），将 绕着点 旋转到 ，连接 ，当 时，四边形 的面积为    ． （4分）某种新式服装原先的利润率为 ，为了促销，现降价 元销售，此时利润率下降为 ，则该种服装每件的进价是     元． （4分）已知数轴上有两点 ，， 表示的数为 ， 表示的数为 ，若动点 从点 出发，经过 次跳动，回到 点，要求从 到 的每个整数点都跳到一次（包括 ， 两点），且每次跳跃均尽可能最大，设跳过的所有路程之和为 ，则     ． （4分）如图，点 ， 在双曲线 上，连接 ，，以 ， 为边作平行四边形 ．若点 恰落在双曲线 上，此时平行四边形 的面积为    ． （4分）已知正方形 与正 都内接于圆 ，若正方形边长为 ，则     ． （4分）如图，在平行四边形 中，， 是 的中点，作 ，垂足 在线段 上，连接 ，，则下列结论：（）；（）；（）；（）若 ，则 ．其中一定成立的是    （把所有正确结论的序号都填在横线上） 三、解答题（62分）（6分）新成药业集团研究开发了一种新药，在实验药效时发现，如果儿童按规定剂量服用，那么 的时候血液中含药量最高，接着逐步衰减，每毫升血液中含药量 （微克）随时间 的变化如图所示，当儿童按规定剂量服药后：(1)  何时血液中含药量最高？是多少微克？(2)  点 表示什么意义？(3)  每毫升血液中含药量为 微克以上时在治疗疾病时是有效的，那么这个有效期是多长？(4)  你建议儿童首次服药后几小时再服药？为什么？ （6分）计算：(1)   ；(2)   ． （6分）计算：． （8分）为响应国家节能减排的号召，鼓励人们节约用电，保护能源，某市实施用电“阶梯价格”收费制度．收费标准如表：已知小刚家上半年的用电情况如下表（以 度为标准，超出 度记为正、低于 度记为负）：根据上述数据，解答下列问题：(1)  小刚家用电量最多的是    月份，实际用电量为    度；(2)  小刚家一月份应交纳电费    元；(3)  若小刚家七月份用电量为 度，求小刚家七月份应交纳的电费（用含 的代数式表示）． （8分）如图，矩形 在平面直角坐标系中，并且 、 的长满足：．(1)  求 、 、 三点的坐标．(2)  把 沿 对折，点 落在点 处， 与 轴交于点 ，求直线 的解析式．(3)  在直线 上是否存在点 使 的值最小？若存在，请找出点 的位置，并求出 的最小值；若不存在，请说明理由．(4)  在直线 上是否存在点 使 的值最大？若存在，请找出点 的位置，并求出 的最大值． （8分）如图，在四边形 中，，以 为直径的 交 于点 ，交 于点 ，．(1)  求证： 与 相切；(2)  若 ．①求证：；②若 ，，则     ． （10分）如图，四边形 是矩形，点 是对角线 上一动点（不与点 和点 重合），连接 ，过点 作 交射线 于点 ，连接 ．已知 ，，设 的长为 ．(1)  线段 的最小值    ，当 时，     ；(2)  如图，当动点 运动到 的中点时， 与 的交点为 ， 的中点为 ，求线段 的长度；(3)  当点 在运动的过程中：①试探究 是否会发生变化？若不改变，请求出 大小；若改变，请说明理由；②当 为何值时， 是等腰三角形？ （10分）阅读下列两则材料，回答问题．材料一：我们将 与 称为一对“对偶式”． ，  构造“对俩式”相乘可以有效地将 和 中的“”去掉．例如：已知 ，求 的值．解：． ， ．材料二：如图，点 ，点 ，以 为斜边作 ，则 ，于是 ，， ．反之，可将代数式 的值看作点 到点 的距离．例如    可将代数式 的值看作点 到点 的距离．(1)  利用材料一，解关于 的方程：，其中 ；(2)  ①利用材料二，求代数式 的最小值，并求出此时 与 的函数关系式，写出 的取值范围；②将①所得的 与 的函数关系式和 的取值范围代入 中解出 ，直接写出 的值．
答案一、选择题（30分）1.  【答案】B【解析】 ， ， ， ， ．【知识点】圆周角定理及其推理 2.  【答案】A【解析】①如图 中，连接 ，延长 交 于 ．由旋转的性质得：， ，， ，， ， ， ，由翻折可知：，，，  垂直平分线段 ， ，故①正确， ②如图 中，当 ，， 共线时， ，， ， ，在 上取一点 ，使得 ，连接 ， ， ， ，设 ，则 ，则有 ， ， ，故②正确，③如图 中，连接 ，，当 时，设 ，则有：，  或 （舍弃）， ，故③正确，④如图 中，当 时，设 ． ，， ， ， ， ， ，或 （舍去）， ，故④正确．故选：．【知识点】旋转及其性质 3.  【答案】D【解析】将线段 向右平移 个单位，得点 的对应点的坐标为 ，将所得线段绕原点按顺时针方向旋转 ，得 的坐标为 ．【知识点】坐标平面内图形的旋转变换、图形的平移 4.  【答案】C【知识点】勾股定理之折叠问题、图形成轴对称 5.  【答案】B【解析】 ， ，  是 边上的垂直平分线， ， ，同理，， ， ，故选 ．【知识点】垂直平分线的性质 6.  【答案】C【解析】由题意可知：，，．当 时，． ， ，即 ．  当 时，此时 ， ，即 ，．【知识点】二次函数的图象与性质 7.  【答案】D【知识点】一般三角形面积公式、勾股定理、正方形的性质、角边角、正弦 8.  【答案】D【解析】分析图象可以发现，点 的运动每 次位置循环一次．每循环一次向右移动四个单位． ，当第 循环结束时，点 位置在 ，在此基础之上运动三次到 ，故选D．【知识点】平面直角坐标系及点的坐标 9.  【答案】A【解析】【分析】先根据关于轴对称的点的坐标特征确定'的坐标为，，然后把的坐标代入中即可得到的值． 【解析】解：点，关于轴的对称点'的坐标为，，把，代入得．故选：． 【点评】本题考查了反比例函数图象上点的坐标特征：反比例函数为常数，的图象是双曲线，图象上的点，的横纵坐标的积是定值，即．【知识点】k对反比例函数的图象及性质的影响 10.  【答案】C【解析】【分析】用最高温度减去最低温度，结果最大的即为所求； 【解析】解：星期一温差℃；星期二温差℃；星期三温差℃；星期四温差℃；故选：． 【点评】本题考查有理数的减法；能够理解题意，准确计算有理数减法是解题的关键．【知识点】有理数的减法法则及计算 二、填空题（28分）11.  【答案】 【解析】因为 ，，所以 ，即 的小数部分 ．因为 ，所以 的整数部分 ，小数部分 ，则  【知识点】实数的简单运算 12.  【答案】 【解析】如图（），过点 作 交 的延长线于 ．由翻折得 ． ， ， ， ， ， ，  是矩形，， ，，， ， ，  【知识点】勾股定理 13.  【答案】 【解析】设该种服装每件的进价是 元，则原来的销售价为 ，根据题意得：，解得：，答：该种服装每件的进价是 元．故答案是：．【知识点】利润问题 14.  【答案】 【解析】将 ， 之间的各个整点记为 ，，  则跳跃规律为 ，而 表示 又 表示的为 ， 表示的数为 ，每次路程递减 ，则 ．【知识点】有理数加法的应用 15.  【答案】 【解析】如图，连接 ，过 作 轴于 ，过 作 轴于 ，过 作 于 ，则 ，设 ，，则 ，，   ，又 点 在双曲线 上，   ，   ，设 ，则方程 可化为 ，解得 或 （舍去），   ，，   【知识点】反比例函数系数k的几何意义、平行四边形及其性质、反比例函数的解析式 16.  【答案】  【解析】如图，连接 ，，，，  四边形 是正方形， ，，  和 是 的直径， ，  正方形边长为 ， ， ，过 作 于 ， ，  是等边三角形， ， ， ．【知识点】垂径定理、正多边形的有关计算 17.  【答案】（）（）（）【解析】（） 是 的中点， ，  在平行四边形 中，， ， ， ， ，， ， ， ，故（）正确；（）延长 ，交 延长线于 ，如图所示：  四边形 是平行四边形， ， ，  为 中点， ，在 和 中，   ， ，， ， ， ， ， ， ， ，故（）正确；（）， ， ， ．故（）错误；（）， ， ， ， ， ， ，故（）正确．【知识点】性质与判定综合(D) 三、解答题（62分）18.  【答案】(1)  由图可知，服药 后，含药量最高为 微克． (2)   表示 后药效为 ．(3)  由图可知，当服药 至 之间，含药量在 微克以上，因此有效期为 ． (4)  建议首次服药 后再服用，这样保证持续药效． 【知识点】用函数图象表示实际问题中的函数关系 19.  【答案】(1)   (2)   【知识点】二次根式的混合运算 20.  【答案】 【知识点】有理数加减乘除混合运算 21.  【答案】(1)  五； (2)   (3)  当 时，电费为 元；当 时，电费为 元；当 时，电费为  【解析】(1)  由表格可知，五月份用电量最多，实际用电量为：（度）．(2)  小刚家一月份用电：（度），小刚家一月份应交纳电费：（元）．【知识点】简单列代数式、有理数乘法的应用、有理数加法的应用 22.  【答案】(1)  因为 ．所以 ，，所以 ，，因为四边形 为矩形，所以 ，所以 ；(2)  设直线 的解析式为 ，把 、 坐标代入可得 ，解得 所以直线 的解析式为 ．由折叠的性质可知 ，所以可设直线 的解析式为 ，把 点坐标代入可得 ，解得 ，所以直线 的解析式为 ；(3)  存在.由（2）可知 和 关于直线 对称，如图，连接 交 于点 ，则 ，所以 ，所以此时 最小，由折叠的性质可知 ，，在 和 中，，所以 （），所以 ，，设 ，则 ，且 ，在 中，由勾股定理可得 ，即 ，解得 ，所以 ，在 中，由勾股定理可得 ，综上可知存在使 的值最小的点 ， 的最小值为 ；(4)  存在.如图，连接 、 、 ，当 在点 时 最大， 与 对称，，根据三角形三边关系 小于或等于 ，故 的最大值等于 ．因为 ，，所以 ，所以在直线 上，存在点 使 的值最大，最大值为 ．【知识点】三角形的三边关系、一次函数的解析式、轴对称图形、k,b对一次函数图象及性质的影响、轴对称之最短路径、矩形的性质 23.  【答案】(1)  连接 ．  是 的直径， ， ，即 ，且 ， ， ，即 ，且 点 在 上，  与 相切．(2)  ①连接 ． ， 是 的直径， ， ，，  垂直平分 ， ， ， ， ， ， ，且 ， ， ， ．② 【解析】(2)  ②连接 ． ， ． ． ． ， ． ． ， ． ．【知识点】圆周角定理及其推理、两角分别相等、切线的判定 24.  【答案】(1)   ；  (2)  在 中，， ， ，  为等边三角形， ，在 和 中，   ， ，， ，在 中，， ． (3)  ① ．理由如下：由（）可知，， ， ， ；②当 时，，  为等边三角形， ， ，当 时，，不合题意；当 时，， ， ，即 ．综上所述， 时， 是等腰三角形． 【解析】(1)   四边形 是矩形， ， ，当 时，线段 的值最小， ，即 ，解得，，过点 作 交 于 ，交 于 ，则 ， ， ，即 ，解得 ，， ，， ，， ， ， ， ．【知识点】基本定理、矩形的性质、解直角三角形、斜边、直角边、正切、对应边成比例、直角三角形斜边的中线、等腰三角形的判定、两角分别相等 25.  【答案】(1)  根据材料一： ， ， ， ，，  解得：， ． (2)  ①由材料二知：      可将 的值看作点 到点 的距离，  的值看作点 到点 的距离，    当代数式 取最小值，即点 与点 ， 在同一条直线上，并且点 位点 ， 的中间，  的最小值 ，且 ，设过 ，， 的直线解析式为：   解得：  ．② 的值为 ． 【解析】(2)  ② 中， ，  又    由① ②式得：，解得：（舍），，  的值为 ．【知识点】无理方程的解法