初中数学人教版八年级上册14.2.1 平方差公式教案

这是一份初中数学人教版八年级上册14.2.1 平方差公式教案，共8页。教案主要包含了课时安排，教学对象，授课教师，教学目标，教学重点，教学难点，教学方法，教学手段等内容，欢迎下载使用。

【教材】 人教版八年级数学上册第107页至108页. 【课时安排】 1个课时.
【教学对象】 八年级（上）学生.【授课教师】 扶沟县曹里初中 顾兴军.
【教学目标】
知识与技能
（1）理解平方差公式的本质，即结构的不变性，字母的可变性；
（2）达到正用公式的水平，形成正向产生式：
“﹙□+△﹚﹙□– △﹚”→“□² – △²”.
过程与方法
（1）使学生经历公式的独立建构过程，构建以数的眼光看式子的数学素养；
（2）培养学生抽象概括的能力；
（3）培养学生的问题解决能力，为学生提供运用平方差公式来研究等周问题的探究空间。
情感态度价值观
纠正片面观点： “数学只是一些枯燥的公式、规定，没有什么实际意义！学了数学没有用！”体会数学源于实际，高于实际，运用于实际的科学价值与文化价值。
【教学重点】 1.平方差公式的本质的理解与运用；2.数学是什么。
【教学难点】 平方差公式的本质，即结构的不变性，字母的可变性。
【教学方法】 讲练结合、讨论交流。【教学手段】计算机、PPT、flash。
【教学过程设计】
设计意图：根据著名心理学家桑代克的试误学习理论中的“准备律”，运用该情境，能够让学生在动机上做好准备，对所学内容产生兴趣，使学生在学习前处于对知识的“饥饿状态”，产生一个心理“缺口”，从而激发学生产生弥合心理缺口的学习动力。
教学流程设计
速算王的
“绝招”
通过不同类别的典型例题强化所学的知识，例题安排合理，有层次感，符合学生的认知发展水平。同时给出一组简单练习，让学生体会并且掌握公式的结构，突出重点。
该环节按照分层递进的教学原则，设计A、B、C 三组练习；可以让学生从会做的题开始做起，让每个学生都有可以做的题目，都有发展自己能力的题目，使不同程度的学生通过例题，练习，习题得到不同程度的发展和提高。
设计意图：新课程改革的理念之一就是学习方式的转变。现代学习方式的基本特征包括“体验性”，强调学生亲身去经历、去感悟。让学生从听老师讲推导转向学生自己动手进行数学表示、推导演算，体现“做数学（d mathematics）”的现代数学教育理念。
动手操作
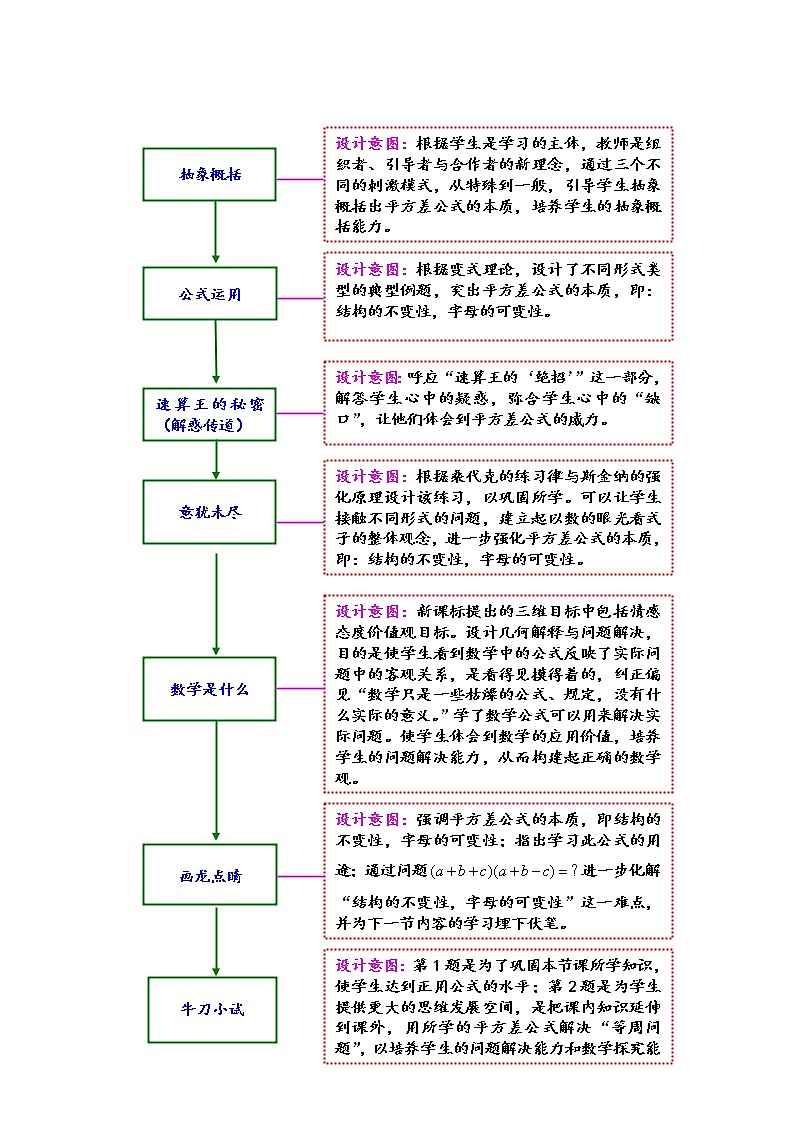
设计意图：根据学生是学习的主体，教师是组织者、引导者与合作者的新理念，通过三个不同的刺激模式，从特殊到一般，引导学生抽象概括出平方差公式的本质，培养学生的抽象概括能力。
抽象概括
设计意图：根据变式理论，设计了不同形式类型的典型例题，突出平方差公式的本质，即：结构的不变性，字母的可变性。
公式运用
速算王的秘密（解惑传道）
设计意图：呼应“速算王的‘绝招’”这一部分，解答学生心中的疑惑，弥合学生心中的“缺口”，让他们体会到平方差公式的威力。
意犹未尽
设计意图：根据桑代克的练习律与斯金纳的强化原理设计该练习，以巩固所学。可以让学生接触不同形式的问题，建立起以数的眼光看式子的整体观念，进一步强化平方差公式的本质，即：结构的不变性，字母的可变性。
设计意图：新课标提出的三维目标中包括情感态度价值观目标。设计几何解释与问题解决，目的是使学生看到数学中的公式反映了实际问题中的客观关系，是看得见摸得着的，纠正偏见“数学只是一些枯燥的公式、规定，没有什么实际的意义。”学了数学公式可以用来解决实际问题。使学生体会到数学的应用价值，培养学生的问题解决能力，从而构建起正确的数学观。
数学是什么
设计意图：强调平方差公式的本质，即结构的不变性，字母的可变性；指出学习此公式的用途；通过问题进一步化解“结构的不变性，字母的可变性”这一难点，并为下一节内容的学习埋下伏笔。
同时为下节课埋下伏笔。
画龙点睛
设计意图：第1题是为了巩固本节课所学知识，使学生达到正用公式的水平；第2题是为学生提供更大的思维发展空间，是把课内知识延伸到课外，用所学的平方差公式解决“等周问题”，以培养学生的问题解决能力和数学探究能力。
牛刀小试
二、教学过程设计
闪光之点
1. 目标创新
(1)理解平方差公式的本质，即结构的不变性，字母的可变性. 这也是数学公式的本质，初步化解了今后大量数学公式学习的难点；
(2)培养“以数的眼光看式子的整体观念”的数学素养;培养学生的问题解决能力和数学探究能力；
(3)纠正片面观点： “数学只是一些枯燥的公式、规定，没有什么实际意义！学了数学没有用！”.
2. 教法创新
从低认知水平的模仿套公式转向高认知水平的学生动手操作,教师引导发现,师生共同抽象概括，形成正向产生式：“﹙□+△﹚﹙□– △﹚”→“□² – △²”.
3. 数学创新
设计了运用平方差公式来解决实际问题解决的例子, 为学生提供运用平方差公式来研究等周问题的探究问题，以培养学生的问题解决能力和数学探究能力,体现了现代数学教育的价值取向.
教学
环节
教 学 内 容
教师
活动
学生
活动
设 计
意 图
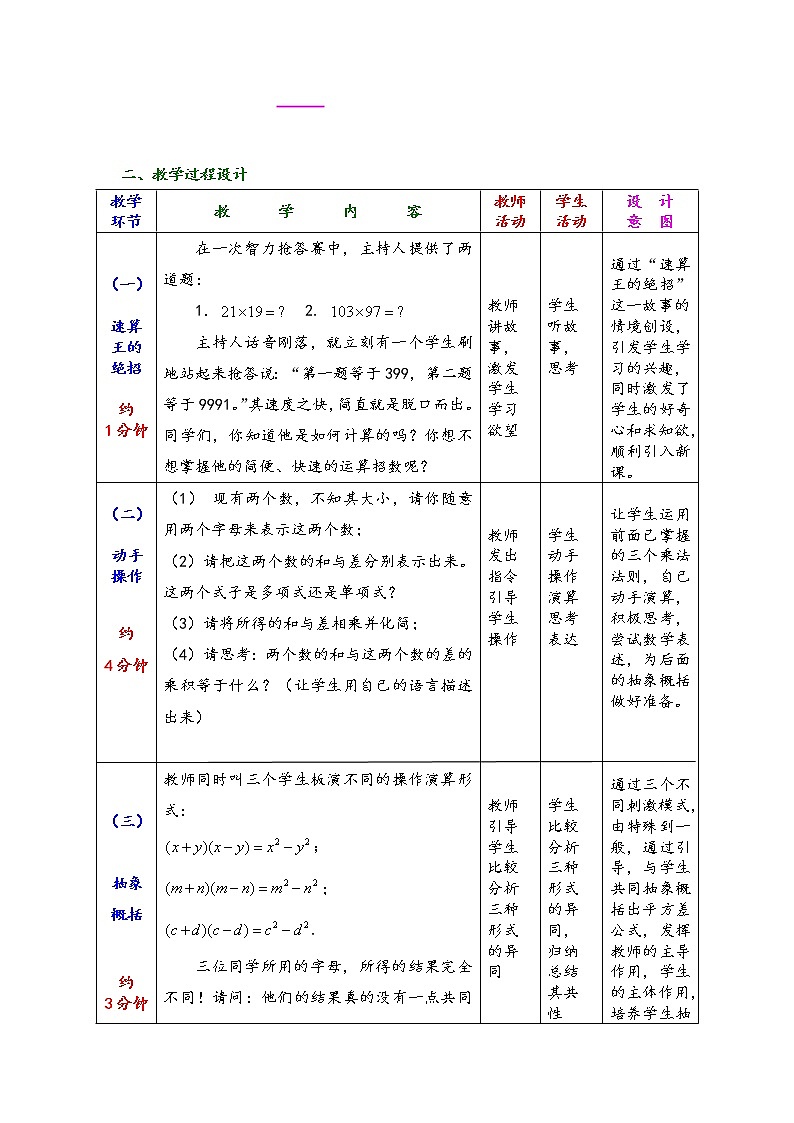
（一）
速算
王的
绝招
约
1分钟
在一次智力抢答赛中，主持人提供了两道题：
1． 2.
主持人话音刚落，就立刻有一个学生刷地站起来抢答说：“第一题等于399，第二题等于9991。”其速度之快，简直就是脱口而出。同学们，你知道他是如何计算的吗？你想不想掌握他的简便、快速的运算招数呢？
教师
讲故
事，
激发
学生
学习
欲望
学生
听故
事，
思考
通过“速算王的绝招”这一故事的
情境创设，引发学生学习的兴趣，
同时激发了学生的好奇心和求知欲，
顺利引入新课。
（二）
动手
操作
约
4分钟
（三）
抽象
概括
约
3分钟
（1） 现有两个数，不知其大小，请你随意用两个字母来表示这两个数；
（2）请把这两个数的和与差分别表示出来。这两个式子是多项式还是单项式？
（3）请将所得的和与差相乘并化简；
（4）请思考：两个数的和与这两个数的差的乘积等于什么？（让学生用自己的语言描述出来）
教师同时叫三个学生板演不同的操作演算形式：
；
；
.
三位同学所用的字母，所得的结果完全不同！请问：他们的结果真的没有一点共同之处吗？引导学生横向比较三个结果，抽象概括出它们的共同结构：“两个数的和与这两个数的差的乘积等于这两个数的平方之差.”
它就是整式乘法的一个乘法公式——平方差公式（frmula fr the difference f squares）：
教师
发出
指令
引导
学生
操作
教师
引导
学生
比较
分析
三种
形式
的异
同
学生
动手
操作
演算
思考
表达
学生
比较
分析
三种
形式
的异
同，
归纳
总结
其共
性
让学生运用前面已掌握的三个乘法法则，自己动手演算，积极思考，尝试数学表述，为后面的抽象概括做好准备。
通过三个不同刺激模式，由特殊到一般，通过引导，与学生共同抽象概括出平方差公式，发挥教师的主导作用，学生的主体作用，培养学生抽象概括能力。
（四）
公式
运用
约
10分钟
（五）
速算
王的
秘密
解
惑
传 道
约
1分钟
（六）
意犹
未尽
约
8分钟
例1 运用平方差公式计算：
（1）；（2）；
（3）；
（4）.
分析：引导学生识别出它们都是两个数的和与这两个数的差的乘积的形式。
练习：第153页的练习第1题.
1.下面各式的计算对不对？如果不对，应当怎样改正？
（1）；
.
2.
解：103×97
=（100+3）（100-3）
=
=9991.
课堂练习: P153练习第2题
2.运用平方差公式计算：
（1）；
（2）；
（3）；
（4）.
教师
引导
学生
以数
的眼
光去
看式
子，
进行
分析
讲解
教师
引导
教师
引导
讲解
教师
巡视
观察
进行
个别
辅导
学生
思考
识别
解决
问题
学生
思考
回答
问题
学生
听讲
思考
学生
自己
思考
做题
1. 根据变式理论，设计了不同形式类型的典型例题，强化平方差公式的本质：即结构的不变性，字母的可变性。
2.这组练习主要是要考察学生有没有掌握平方差公式的结构。
呼应“速算王的‘绝招’”这一部分，解答学生心中的疑惑，弥合学生心中的“缺口”，让他们体会到平方差公式的威力。
根据桑代克的练习律与斯金纳的强化原理设计该练习，以巩固所学。可以让学生接触不同形式的问题，建立起以数的眼光看式子的整体观念，进一步强化平方差公式的本质，即：结构的不变性，字母的可变性。
(七)
数学是
什么
约
8分钟
有人说，数学只是一些枯燥的公式、规定，没有什么实际意义！请问数学真的没有什么实际意义吗？ 请看下面的问题：
1.几何解释：
（1）请表示图(1)中阴影部分的面积.
（2）将阴影部分拼成了一个长方形（图2），这个长方形的长和宽分别是多少？你能表示出它的面积吗？
（3）比较前两问的结果，你有什么发现?
（1） （2）
还有人说，学了数学没有用！果真如此吗？请看
2. 问题解决
宏业住宅小区的花园，起初被设计为边长
为米的正方形，后因道路的原因，设计修改为：北边往南平移2.5米，而东边往东平移2.5米. 试问修改后的花园面积和原先设计的花园面积相差多少？
解：如图（1），原花园的面积.

（1） （2）
修改后的花园如图（2）所示，其面积
.
所以，(m²).
答：修改后的花园面积比修改前少了6.25平方米.
教师
引导
分析
讲解
演示
教师
引导
分析
讲解
演示
学生
观察
思考
领悟
学生
听讲
思考
观察
新课标提出的三维目标中包括情感态度价值观目标。
设计几何解释，目的是使学生看到数学中的公式反映了实际问题中的客观关系，是看得见摸得着的，纠正 “数学只是一些枯燥的公式、规定，没有什么实际的意义。”这样的偏见。
设计问题解决的目的，一是培养学生的问题解决能力；二是使学生知道，学了数学公式，可以用来解决实际问题，从而体会到数学的应用价值，并构建起正确的数学观。
（八）
画龙
点睛
约
4分钟
1.平方差公式的本质：
（1）结构是稳定不变的，即：只要是两个数的和与这两个数的差的乘积，就一定等于这两个数的平方之差.
（2）公式中的字母和却可以变脸！可以是其它字母，可以是正数，也可以是负数；可以是单项式，也可以多项式.
2.我们为什么要学习平方差公式，学了它我们能做什么呢？
在进行某些乘法运算时，利用平方差公式，可以进行简便、快速运算.
计算：
解：
那么如何计算也就是说，如何计算两数和的完全平方呢？让我们共同期待下一次数学课的到来！
教师
引导
总结
教师
启发
学生
以数
的眼
光看
字母
式子
学生
思考
体会
学生
识别
出这
是
两数
和与
两数
差的
乘积
的结
构
让学生看到公式的本质所在，能突破公式字面意义的局限性，建立起较高层次的有意义条件反射，而不是机械的记忆公式。
点明学习平方差公式的必要性。
进一步化解“结构的稳定性，字母的可变性”这一难点，并为下一节内容的学习埋下伏笔。
（九）
牛刀
小试
即
布置
家庭
作业
约
1分钟
家庭作业: P156
1. 牛刀小试
运用平方差公式计算：
（1）；（2）；
（3）；（4）；
（5）；（6）.
2. 数学探究——等周问题
宏业住宅小区的花园，起初被设计为边长
为米的正方形，后因道路的原因，设计修改为：北边往南平移米，而西边往西平移米. 试问：
（1）修改后的花园面积和原先设计的花园面积相差多少？
（2）上述两种设计的面积之差与的大小有什么关系？
（3）在周长为定值4的矩形中，什么时候其面积最大？
（4）计算周长均为4的圆的面积，正六边形的面积。由此你有什么新的发现？
教师
布置
作业
教师
解释
问题
学生
认真
纪录
学生
思考
问题
由浅入深的练习和灵活的变式练习，能够强化本节课所学知识。
该环节为学生提供更大的思维发展空间，是把课内知识延伸到课外，用所学的平方差公式解决“等周问题”，以培养学生的问题解决能力和数学探究能力。