2020-2021学年8.6 空间直线、平面的垂直优秀学案

这是一份2020-2021学年8.6 空间直线、平面的垂直优秀学案，共6页。
1．设m，n是不同的直线，α，β是不同的平面，已知m∥α，n⊥β，下列说法正确的是( )
A．若m⊥n，则α⊥β B．若m∥n，则α⊥β
C．若m⊥n，则α∥β D．若m∥n，则α∥β
2.
如图所示，在三棱锥P ­ ABC中，PA⊥平面ABC，∠BAC＝90°，则二面角B ­ PA ­ C的大小为( )
A．90° B．60°
C．45° D．30°
3.
如图，设P是正方形ABCD外一点，且PA⊥平面ABCD，则平面PAB与平面PBC、平面PAD的位置关系是( )
A．平面PAB与平面PBC、平面PAD都垂直
B．它们两两垂直
C．平面PAB与平面PBC垂直，与平面PAD不垂直
D．平面PAB与平面PBC、平面PAD都不垂直
4．正四棱锥的底面边长为2，侧棱长为eq \r(3)，则侧面与底面所成二面角的大小为________．
5．已知a，b，c为三条不同的直线，α，β，γ为三个不同的平面，给出下列命题：
①若α⊥β，β⊥γ，则α∥γ；②若a⊂α，b⊂β，c⊂β，a⊥b，a⊥c，则α⊥β；③若a⊥α，b⊂β，a∥b，则α⊥β.
其中不正确的命题是________．
6．如图，在圆锥PO中，AB是⊙O的直径，C是上的点，D为AC的中点．证明：平面POD⊥平面PAC.
[提能力]
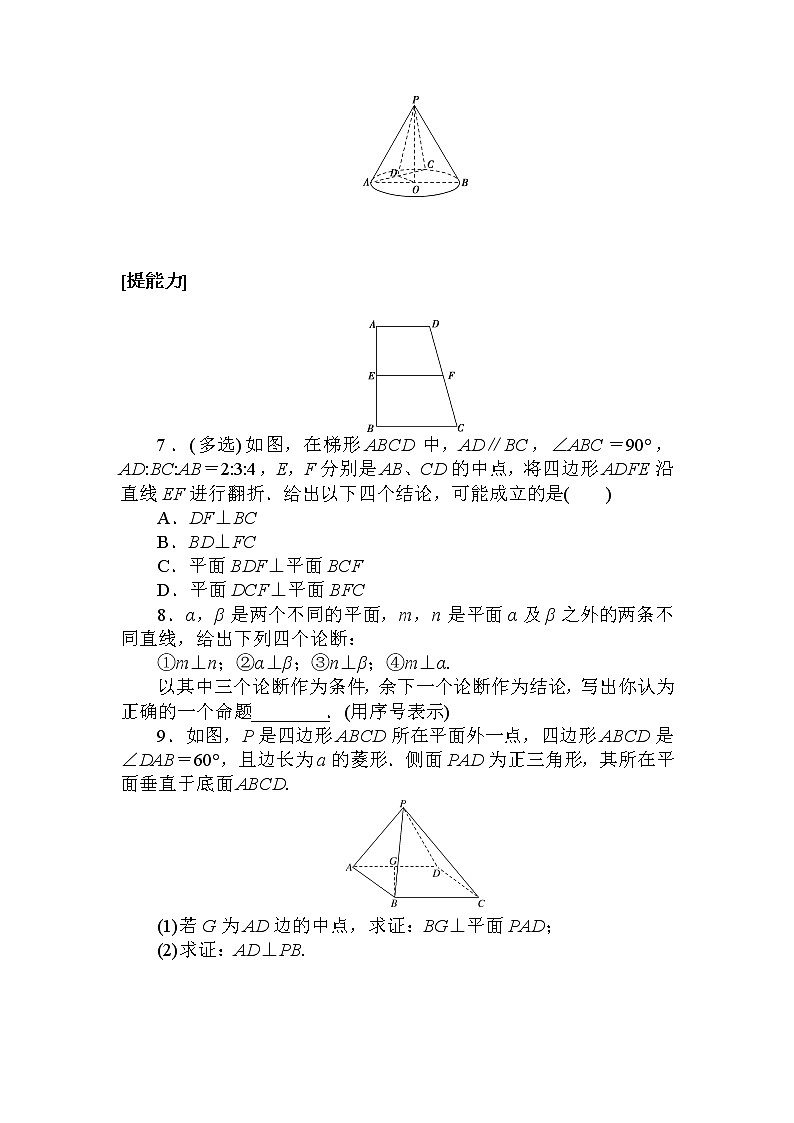
7．(多选)如图，在梯形ABCD中，AD∥BC，∠ABC＝90°，AD:BC:AB＝2:3:4，E，F分别是AB、CD的中点，将四边形ADFE沿直线EF进行翻折．给出以下四个结论，可能成立的是( )
A．DF⊥BC
B．BD⊥FC
C．平面BDF⊥平面BCF
D．平面DCF⊥平面BFC
8．α，β是两个不同的平面，m，n是平面α及β之外的两条不同直线，给出下列四个论断：
①m⊥n；②α⊥β；③n⊥β；④m⊥α.
以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题________．(用序号表示)
9．如图，P是四边形ABCD所在平面外一点，四边形ABCD是∠DAB＝60°，且边长为a的菱形．侧面PAD为正三角形，其所在平面垂直于底面ABCD.
(1)若G为AD边的中点，求证：BG⊥平面PAD；
(2)求证：AD⊥PB.
[战疑难]
10．如图，在三棱锥P ­ ABC中，△PAC，△ABC都是边长为6的等边三角形，若二面角P ­ AC ­ B的大小为120°，则三棱锥P ­ ABC的外接球的表面积为________．
课时作业解析
1．解析：若m⊥n，则α与β可以平行或相交，故A，C错误；若m∥n，则α⊥β，D错，选B.
答案：B
2．解析：∵PA⊥平面ABC，BA，CA⊂平面ABC，
∴BA⊥PA，CA⊥PA，因此，∠BAC即为二面角B ­ PA ­ C的平面角．又∠BAC＝90°，故选A.
答案：A
3．解析：∵PA⊥平面ABCD，BC，AD⊂平面ABCD，
∴PA⊥BC，PA⊥AD.
又∵BC⊥AB，PA∩AB＝A，∴BC⊥平面PAB.
∵BC⊂平面PBC，∴平面PBC⊥平面PAB.
由AD⊥PA，AD⊥AB，PA∩AB＝A，得AD⊥平面PAB.
∵AD⊂平面PAD，∴平面PAD⊥平面PAB.显然平面PAD与平面PBC不垂直．故选A.
答案：A
4．解析：如图，设S在底面内的射影为O，
取AB的中点M，
连接OM，SM，
则∠SMO为所求二面角的平面角，
在Rt△SOM中，
OM＝eq \f(1,2)AD＝1，
SM＝ eq \r(SA2－\f(1,4)AB2)＝eq \r(2)，
所以cs∠SMO＝eq \f(OM,SM)＝eq \f(\r(2),2)，
所以∠SMO＝45°.
答案：45°
5.
解析：如图，在长方体ABCD ­ A1B1C1D1中，记平面ADD1A1为α，平面ABCD为β，平面ABB1A1为γ，显然①错误；②只有在直线b，c相交的情况下才成立；易知③正确．
答案：①②
6．证明：如图，连接OC，因为OA＝OC，
D是AC的中点，所以AC⊥OD.
又PO⊥底面AOC，AC⊂底面AOC，所以AC⊥PO.因为OD，PO是平面POD内的两条相交直线，所以AC⊥平面POD.又AC⊂平面PAC，所以平面POD⊥平面PAC.
7.
解析：对于A，因为BC∥AD，AD与DF相交，不垂直，所以BC与DF不垂直，故A不可能成立；对于B，如图，设点D在平面BCF上的射影为点P，当BP⊥CF时，有BD⊥FC，而AD:BC:AB＝2:3:4可使条件满足，故B可能成立；对于C，当点P落在BF上时，DP⊂平面BDF，从而平面BDF⊥平面BCF，故C可能成立；对于D，因为点D的射影不可能在FC上，所以D不可能成立．故选BC.
答案：BC
8．解析：m⊥n，将m和n平移到相交的位置，此时确定一平面，
∵n⊥β，m⊥α，
∴该平面与平面α和平面β的交线也互相垂直，
从而平面α和平面β形成的二面角的平面角为90°，∴α⊥β.
故①③④⇒②.
答案：①③④⇒②(答案不唯一)
9.
证明：(1)如图所示，连接BD.
因为四边形ABCD是菱形，且∠DAB＝60°，
所以△ABD是正三角形，
因为G是AD的中点，
所以BG⊥AD.
又因为平面PAD⊥平面ABCD，
平面PAD∩平面ABCD＝AD，BG⊂平面ABCD.
所以BG⊥平面PAD.
(2)连接PG.
因为△PAD为正三角形，G为AD的中点，
所以PG⊥AD.
由(1)知BG⊥AD，
而PG∩BG＝G，
PG⊂平面PBG，
BG⊂平面PBG，
所以AD⊥平面PBG.
又因为PB⊂平面PBG，
所以AD⊥PB.
10.
解析：如图，取AC的中点D，连接DP，DB.
由△PAC，△ABC都是边长为6的等边三角形，得PD⊥AC，BD⊥AC，所以∠PDB为二面角P ­ AC ­ B的平面角，则∠PDB＝120°.
设O为三棱锥P ­ ABC外接球的球心，O1，O2分别为△ABC，△PAC的中心，
则OO1⊥平面ABC，OO2⊥平面PAC，且O2D＝O1D＝eq \f(1,3)×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)×6))＝eq \r(3)，OO2＝OO1.
易知O，O2，D，O1四点共面，连接OD，则∠ODO1＝60°，OO1＝eq \r(3)DO1＝3.
连接OB，则三棱锥P ­ ABC的外接球半径R＝OB＝eq \r(OO\\al(2,1)＋O1B2)＝eq \r(32＋2\r(3)2)＝eq \r(21).
所以三棱锥P ­ ABC的外接球的表面积为4πR2＝84π.
答案：84π