数学七年级下册第五章 相交线与平行线综合与测试单元测试同步测试题

这是一份数学七年级下册第五章 相交线与平行线综合与测试单元测试同步测试题，共14页。试卷主要包含了 选择题， 填空题， 解答题等内容，欢迎下载使用。

一、 选择题 （本题共计 7 小题 ，每题 4 分 ，共计28分 ， ）

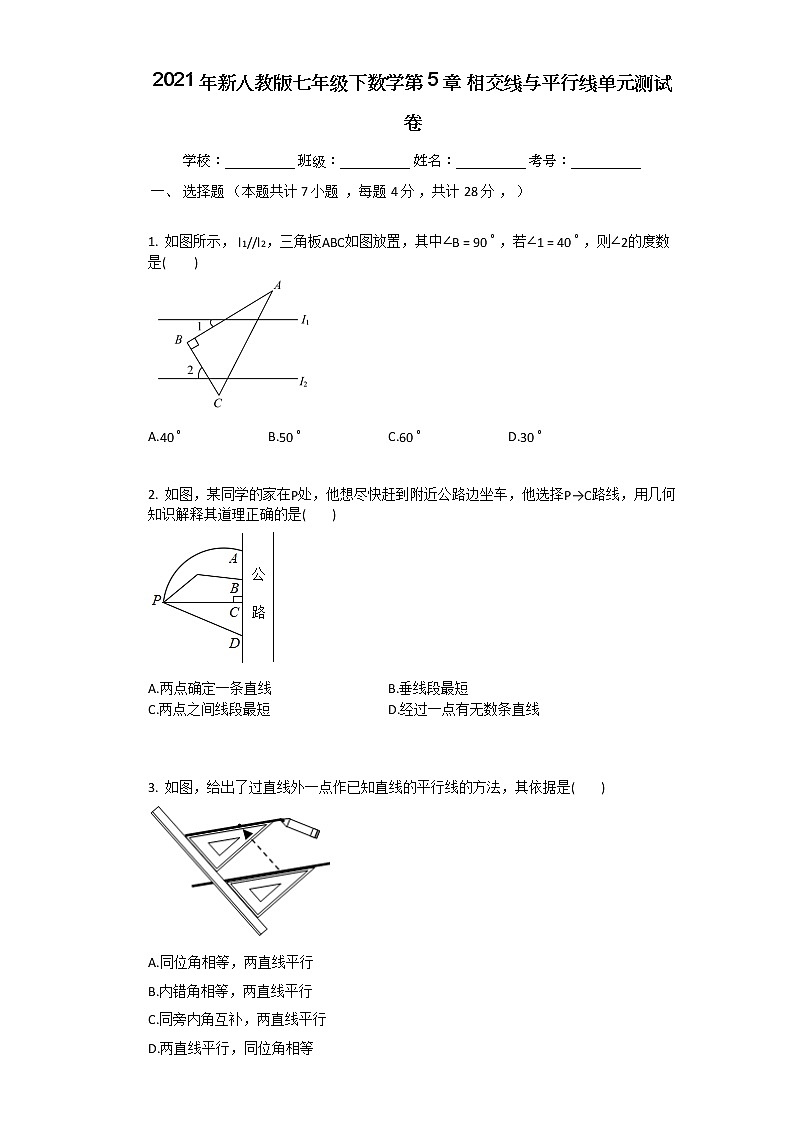
1. 如图所示， l1//l2，三角板ABC如图放置，其中∠B=90∘ ，若∠1=40∘ ，则∠2的度数是( )

A.40∘B.50∘C.60∘D.30∘

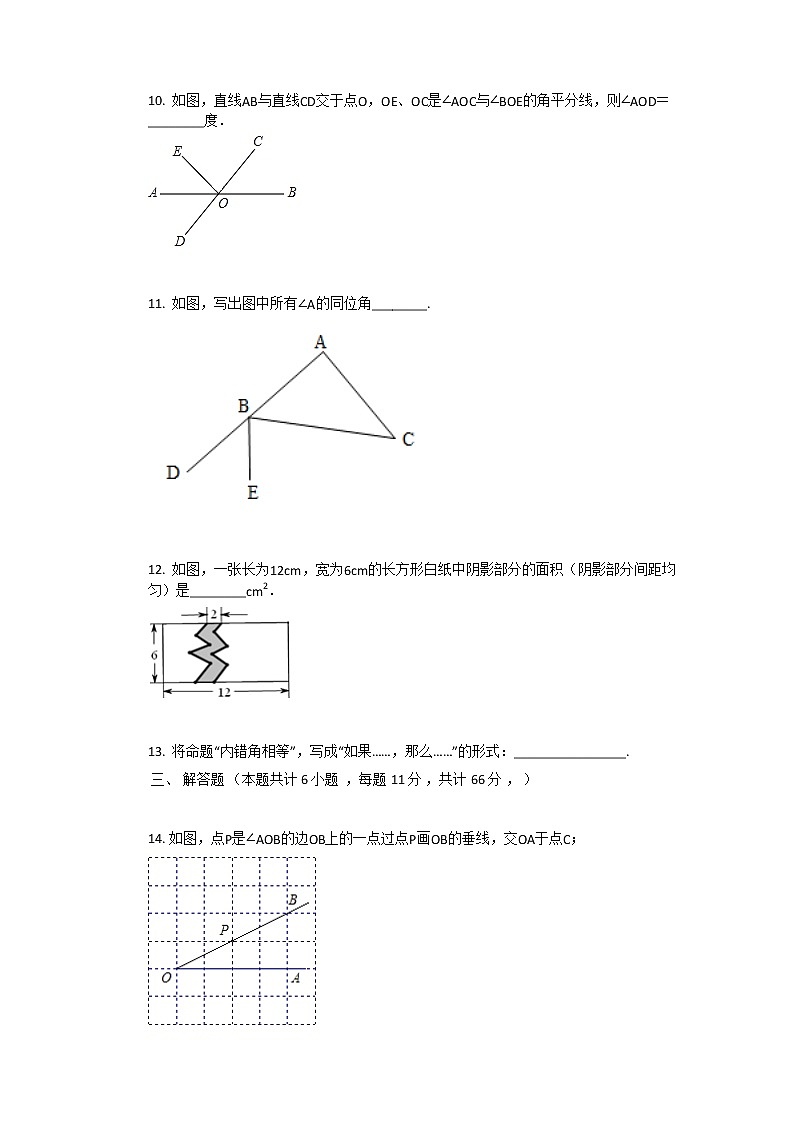
2. 如图，某同学的家在P处，他想尽快赶到附近公路边坐车，他选择P→C路线，用几何知识解释其道理正确的是( )

A.两点确定一条直线B.垂线段最短
C.两点之间线段最短D.经过一点有无数条直线

3. 如图，给出了过直线外一点作已知直线的平行线的方法，其依据是( )

A.同位角相等，两直线平行
B.内错角相等，两直线平行
C.同旁内角互补，两直线平行
D.两直线平行，同位角相等

4. 如图，直线AC和直线BD相交于点O，若∠1+∠2=90∘，则∠BOC的度数是( )

A.100∘B.115∘C.135∘D.145∘

5. 平面内有两两相交的4条直线，如果最多有m个交点，最少有n个交点，那么m−n=( )
A.3B.4C.5D.6

6. 在同一平面内，下列说法正确的是( )
A.两直线的位置关系是平行、垂直和相交
B.不平行的两条直线一定互相垂直
C.不垂直的两条直线一定互相平行
D.不相交的两条直线一定互相平行

7. 在同一平面内，两直线的位置关系必是( )
A.相交B.平行C.相交或平行D.垂直
二、 填空题 （本题共计 6 小题 ，每题 4 分 ，共计24分 ， ）

8. 如图所示，将直角三角形ABC沿BC方向平移4cm，得到直角三角形DEF，连接AD，若AB=5cm，则图中阴影部分的面积为________．

9. 如图，直线AB与直线CD垂直于点O，直线EF过点O，已知∠1=29∘，则∠2=________．


10. 如图，直线AB与直线CD交于点O，OE、OC是∠AOC与∠BOE的角平分线，则∠AOD＝________度．


11. 如图，写出图中所有∠A的同位角________.


12. 如图，一张长为12cm，宽为6cm的长方形白纸中阴影部分的面积（阴影部分间距均匀）是________cm2．


13. 将命题“内错角相等”，写成“如果……，那么……”的形式：________________.
三、 解答题 （本题共计 6 小题 ，每题 11 分 ，共计66分 ， ）

14. 如图，点P是∠AOB的边OB上的一点过点P画OB的垂线，交OA于点C；
（1）过点P画OA的垂线，垂足为H；

（2）线段PH的长度是点P到________的距离，________是点C到直线OB的距离．线段PC、PH、OC这三条线段大小关系是________（用“<”号连接）

15. 观察下面的变形规律：
11×2=1−12；12×3=12−13；13×4=13−14；…
解答下面的问题：
1计算15×6=________；

2若n为正整数，请你猜想1n(n+1)=________；

3利用你的结论求：11×2+12×3+13×4+...+19×10．

16. 如图，在△ABC中，AB>AC，点D在边上.

(1)过点D，作平行线DE//BC，交AC于点E.(尺规作图，不写作法，保留作图痕迹)

(2)在上(1)中，若∠B=50∘，∠A=60∘，求∠ADE的度数.

17. 如图所示，有两条宽均为1米的小路穿过长方形的草地ABCD，若AB=60m，BC=84m，若要硬化这两条小路，且每平方米造价50元，则硬化这两条小路需要多少钱？


18. 某学校准备在升旗台的台阶上铺设一种红色的地毯（含台阶的最上层），已知这种地毯的批发价为每平方米40元，升旗台的台阶宽为3米，其侧面如图所示请你帮助测算一下，买地毯至少需要多少元？

19.
(1)问题发现：如图①，直线AB//CD，E是AB与CD之间的一点，连接BE，CE，可以发现∠B+∠C=∠BEC.
请把下面的证明过程补充完整：
证明：过点E作EF//AB，
∵ AB//CD（已知），EF//AB（已作），
∴ EF//CD（________），
∴ ∠C=∠CEF（________）.
∵ EF//AB，
∴ ∠B=________（________），
∵ ∠CEF+∠BEF=∠BEC，
∴ ∠B+∠C=∠BEC（等量代换）．

(2)拓展探究：如果点E运动到图②所示的位置，其他条件不变，进一步探究发现：∠B，∠C，∠BEC之间的关系是________.

(3)解决问题：如图③，AB//DC，∠C=120∘，∠AEC=80∘，请求出∠A的度数．
参考答案与试题解析
2021年新人教版七年级下数学第5章 相交线与平行线单元测试卷
一、 选择题 （本题共计 7 小题 ，每题 4 分 ，共计28分 ）
1.
【答案】
B
【考点】
平行线的判定与性质
【解析】
此题暂无解析
【解答】
解：作BD//l1，如图所示，
∵ BD//l1，∠1=40∘，
∴ ∠1=∠ABD=40∘.
又∵ l1//l2，
∴ BD//l2，
∴ ∠CBD=∠2.
∵ ∠B=∠CBD+∠ABD=90∘，
∴ ∠CBD=50∘，
∴ ∠2=50∘.
故选B.
2.
【答案】
B
【考点】
垂线段最短
【解析】
根据垂线段的性质解答即可．
【解答】
解：某同学的家在P处，他想尽快赶到附近公路边搭顺风车，他选择P→C路线，是因为垂直线段最短.
故选B.
3.
【答案】
A
【考点】
作图—几何作图
平行线的判定
【解析】
判定两条直线是平行线的方法有：可以由内错角相等，两直线平行；同位角相等，两直线平行；同旁内角互补两直线平行等，应结合题意，具体情况，具体分析．
【解答】
解：图中所示过直线外一点作已知直线的平行线，
则利用了同位角相等，两直线平行的判定方法．
故选A．
4.
【答案】
C
【考点】
邻补角
对顶角
【解析】
根据对顶角和邻补角的定义即可得到结论．
【解答】
解：∵ ∠1=∠2，∠1+∠2=90∘，
∴ ∠1=∠2=45∘，
∴ ∠BOC=135∘.
故选C.
5.
【答案】
C
【考点】
相交线
【解析】
可根据题意，画出图形，找出交点最多和最少的个数，求m−n．
【解答】
解：如图所示：
4条直线两两相交，有3种情况：4条直线经过同一点，有一个交点；
3条直线经过同一点，被第4条直线所截，有4个交点；
4条直线不经过同一点，有6个交点．
故平面内两两相交的4条直线，最多有6个交点，最少有1个交点；
即m=6，n=1，则m−n=5．
故选C．
6.
【答案】
D
【考点】
两直线垂直问题
两直线相交非垂直问题
平行线的概念及表示
【解析】
在同一平面内，两直线的位置关系有2种：平行、相交，根据以上结论判断即可．
【解答】
解：A，∵ 在同一平面内，两直线的位置关系是平行、相交，2种；
∴ 在同一平面内，两直线的位置关系是平行、相交（相交不一定垂直），故本选项错误；
B，在同一平面内，不平行的两条直线一定相交，故本选项错误；
C，在同一平面内，不垂直的两直线可能平行，可能相交，故本选项错误；
D，在同一平面内，不相交的两条直线一定平行，故本选项正确.
故选D．
7.
【答案】
C
【考点】
平行线的概念及表示
相交线
【解析】
利用同一个平面内，两条直线的位置关系解答，同一平面内两条直线的位置关系有两种：平行、相交．
【解答】
解：在同一个平面内，两条直线只有两种位置关系，即平行或相交．
故选C．
二、 填空题 （本题共计 6 小题 ，每题 4 分 ，共计24分 ）
8.
【答案】
20cm2
【考点】
平移的性质
【解析】
先判断出阴影部分是平行四边形，再根据平行四边形的面积公式列式计算即可得解．
【解答】
解：∵ Rt△ABC沿BC方向平移得到Rt△DEF，
∴ AC // DF，AC=DF，
∴ 阴影部分四边形ACFD是平行四边形，
∵ 平移距离为4cm，
∴ CF=4cm，
∴ 阴影部分的面积为=CF⋅AB=4×5=20cm2．
故答案为：20cm2．
9.
【答案】
61∘
【考点】
余角和补角
垂线
【解析】
根据∠2=180∘−∠1−∠AOC，即可得解.
【解答】
解：因为AB⊥CD，
所以∠AOC=90∘，
因为∠1=29∘，
所以∠2=180∘−∠1−∠AOC
=180∘−29∘−90∘
=61∘.
故答案为：61∘.
10.
【答案】
60
【考点】
角平分线的定义
对顶角
邻补角
【解析】
根据角平分线、对顶角及互补的定义求出∠AOD的度数．
【解答】
∵ OE、OC是∠AOC与∠BOE的角平分线，
∴ ∠AOE＝∠EOC＝∠BOC=1803=60∘，
∴ ∠AOD＝∠BOC＝60∘．
11.
【答案】
∠DBE，∠DBC
【考点】
同位角、内错角、同旁内角
【解析】
根据同位角的定义分析即可解答.
【解答】
解：∠A的同位角有∠DBE，∠DBC.
故答案为：∠DBE，∠DBC.
12.
【答案】
12
【考点】
生活中的平移现象
【解析】
阴影部分的面积，可看作四个同底平行四边形，根据平行四边形的面积，可得答案．
【解答】
解：阴影部分的面积，可看作四个同底平行四边形，
四个平行四边形的底都是2，高的和是6，
阴影的面积是2×6=12，
故答案为：12．
13.
【答案】
如果两个角是内错角，那么这两个角相等
【考点】
定义、命题、定理、推论的概念
【解析】
根据命题的构成，题设是内错角，结论是这两个角相等写出即可．
【解答】
解：命题“内错角相等”可以写成：如果两个角是内错角，那么这两个角相等．
故答案为：如果两个角是内错角，那么这两个角相等．
三、 解答题 （本题共计 6 小题 ，每题 11 分 ，共计66分 ）
14.
【答案】
OA，线段CP，PHOA,线段CP的长度,PH【考点】
点到直线的距离
垂线段最短
【解析】
（1）过点P画OA的垂线，即过点P画∠PHO=90∘即可，
（2）利用点到直线的距离可以判断线段PH的长度是点P到OA的距离，PC是点C到直线OB的距离，线段PC、PH、OC这三条线段大小关系是PH【解答】
解：（1）如图：
（2）线段PH的长度是点P到直线OA的距离，
线段CP的长度是点C到直线OB的距离，
根据垂线段最短可得：PH15.
【答案】
15−16.
1n−1n+1．
311×2+12×3+13×4+...+19×10
=1−12+12−13+...+19−110
=1−110
=910．
【考点】
推理与论证
有理数的混合运算
【解析】
（1）（2）将分数拆分即可求解；
（3）先将分数拆分，再用抵消法即可求解．
【解答】
解：观察规律可得：
15×6=15−16.
故答案为：15−16 .
21n(n+1)=1n−1n+1.
故答案为：1n−1n+1.
311×2+12×3+13×4+...+19×10
=1−12+12−13+...+19−110
=1−110
=910．
16.
【答案】
解：(1)如图所示，
DE即为所求作的平行线.
(2)∵DE//BC,
∴∠ADE=∠B=50∘（两直线平行，同位角相等）.
【考点】
作图—几何作图
平行线的画法
平行线的性质
【解析】
此题暂无解析
【解答】
解：(1)如图所示，
DE即为所求作的平行线.
(2)∵DE//BC,
∴∠ADE=∠B=50∘（两直线平行，同位角相等）.
17.
【答案】
解：84×60−(84−1)×(60−1)
=143m2.
143×50=7150(元)
答：硬化这两条小路需要7150元钱.
【考点】
生活中的平移现象
【解析】
四边形ABCD是矩形，则AF // EC，又AF=CE，进而可判断四边形AECF的形状，继而面积可以利用底边长乘以高进行计算．
【解答】
解：84×60−(84−1)×(60−1)
=143m2.
143×50=7150(元)
答：硬化这两条小路需要7150元钱.
18.
【答案】
买地毯需要1680元．
【考点】
生活中的平移现象
【解析】
根据题意，结合图形，先把楼梯的横竖向上向左平移，构成一个矩形，再求得其面积，则购买地毯的钱数可求．
【解答】
解：如图：
利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，长宽分别为6.4米，3.8米，
∴ 地毯的长度为6.4+3.8+3.8=14米，地毯的面积为14×3=42平方米，
∴ 买地毯至少需要42×40=1680元．
19.
【答案】
解：(1)证明：过点E作EF//AB，
∵ AB//CD（已知），EF//AB（已作），
∴ EF//CD（平行于同一条直线的两直线平行），
∴ ∠C=∠CEF（两直线平行，内错角相等）.
∵ EF//AB，
∴ ∠B=∠BEF（两直线平行，内错角相等），
∵ ∠CEF+∠BEF=∠BEC，
∴ ∠B+∠C=∠BEC（等量代换）．
∠B+∠C+∠BEC=360∘
(3)如图，过点E作EH//AB//CD，
则∠A=∠AEH，
∠HEC+∠C=180∘，
∴ ∠HEC=180∘−∠C=60∘，
∵ ∠AEC=80∘，
∴ ∠AEH=∠AEC−∠HEC=20∘，
∴ ∠A=∠AEH=20∘.
【考点】
平行公理及推论
平行线的性质
【解析】
.
.
.
【解答】
解：(1)证明：过点E作EF//AB，
∵ AB//CD（已知），EF//AB（已作），
∴ EF//CD（平行于同一条直线的两直线平行），
∴ ∠C=∠CEF（两直线平行，内错角相等）.
∵ EF//AB，
∴ ∠B=∠BEF（两直线平行，内错角相等），
∵ ∠CEF+∠BEF=∠BEC，
∴ ∠B+∠C=∠BEC（等量代换）．
(2)如图，过点E作EG//AB//CD，
则∠B+∠BEG=180∘，∠C+∠CEG=180∘，
又∠BEG+∠CEG=∠BEC，
可得∠B+∠C+∠BEC=360∘.
故答案为：∠B+∠C+∠BEC=360∘.
(3)如图，过点E作EH//AB//CD，
则∠A=∠AEH，
∠HEC+∠C=180∘，
∴ ∠HEC=180∘−∠C=60∘，
∵ ∠AEC=80∘，
∴ ∠AEH=∠AEC−∠HEC=20∘，
∴ ∠A=∠AEH=20∘.