课时跟踪检测（十九） 圆柱、圆锥、圆台、球和简单组合体

这是一份课时跟踪检测（十九） 圆柱、圆锥、圆台、球和简单组合体，共5页。试卷主要包含了如图所示的图形中有，圆柱的母线长为10，则其高等于，有下列四个说法，其中正确的是等内容，欢迎下载使用。

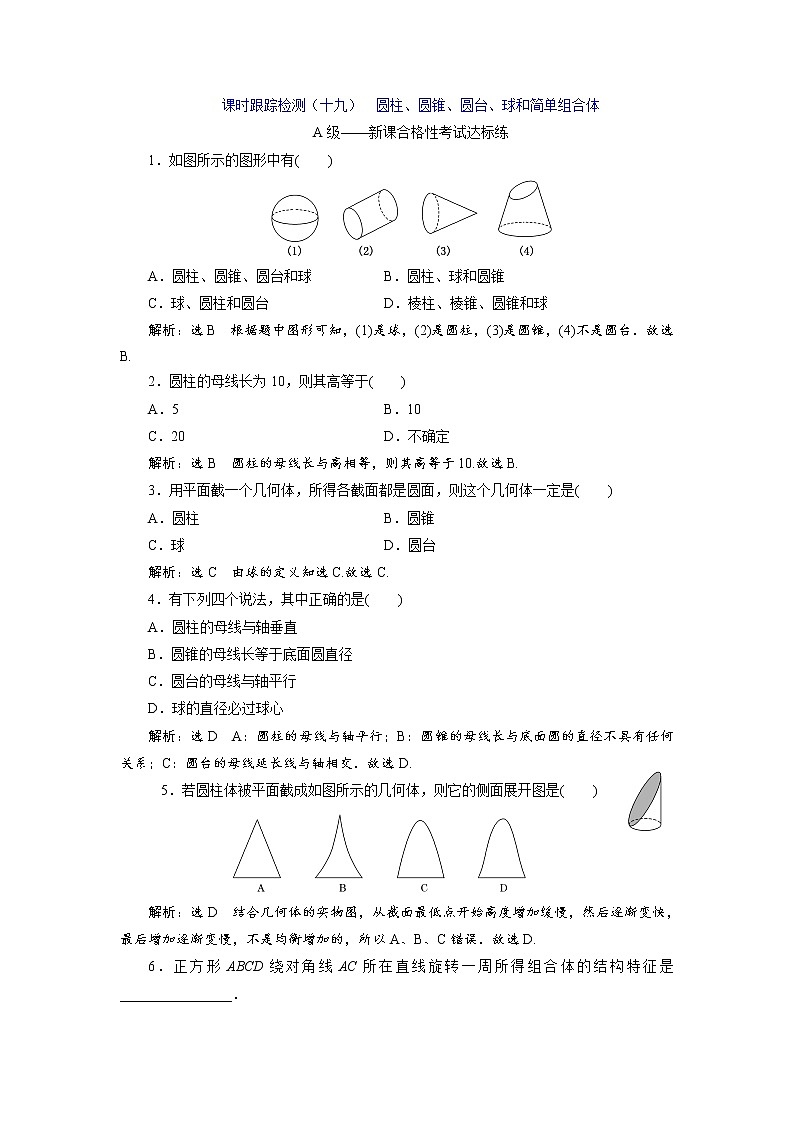
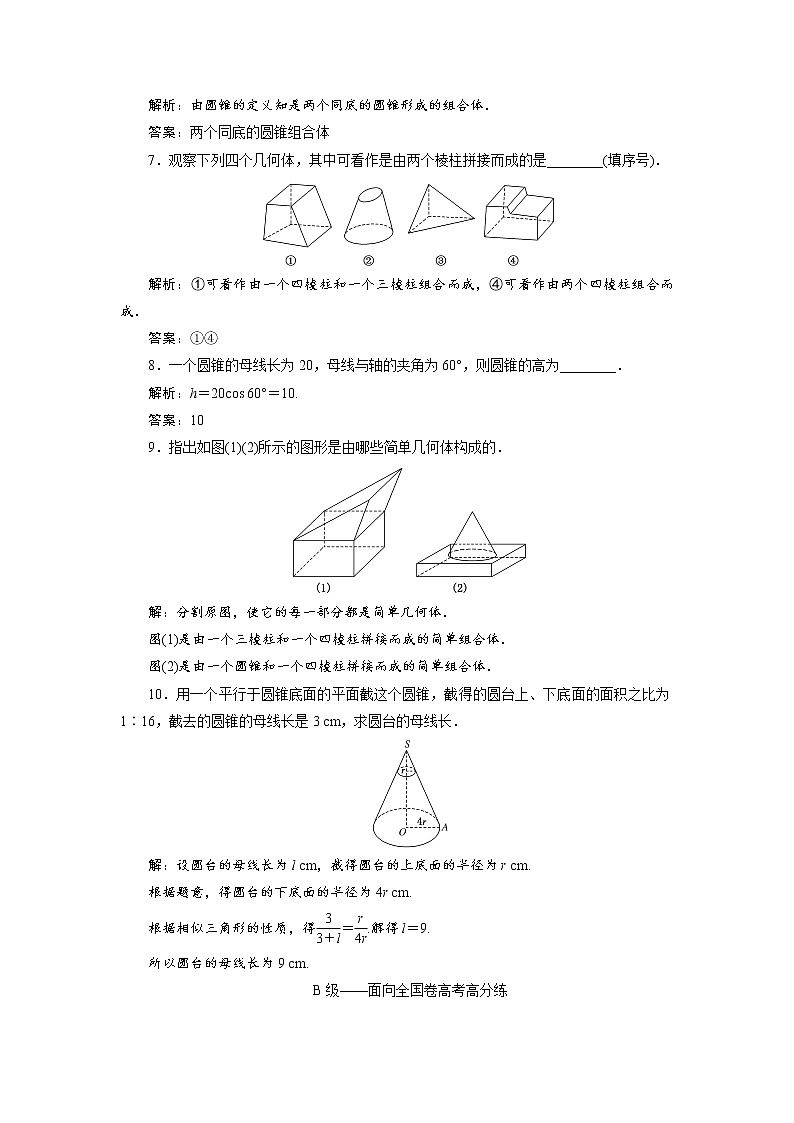
1．如图所示的图形中有( )
A．圆柱、圆锥、圆台和球 B．圆柱、球和圆锥
C．球、圆柱和圆台 D．棱柱、棱锥、圆锥和球
解析：选B 根据题中图形可知，(1)是球，(2)是圆柱，(3)是圆锥，(4)不是圆台．故选B.
2．圆柱的母线长为10，则其高等于( )
A．5 B．10
C．20 D．不确定
解析：选B 圆柱的母线长与高相等，则其高等于10.故选B.
3．用平面截一个几何体，所得各截面都是圆面，则这个几何体一定是( )
A．圆柱 B．圆锥
C．球 D．圆台
解析：选C 由球的定义知选C.故选C.
4．有下列四个说法，其中正确的是( )
A．圆柱的母线与轴垂直
B．圆锥的母线长等于底面圆直径
C．圆台的母线与轴平行
D．球的直径必过球心
解析：选D A：圆柱的母线与轴平行；B：圆锥的母线长与底面圆的直径不具有任何关系；C：圆台的母线延长线与轴相交．故选D.
5．若圆柱体被平面截成如图所示的几何体，则它的侧面展开图是( )
解析：选D 结合几何体的实物图，从截面最低点开始高度增加缓慢，然后逐渐变快，最后增加逐渐变慢，不是均衡增加的，所以A、B、C错误．故选D.
6．正方形ABCD绕对角线AC所在直线旋转一周所得组合体的结构特征是________________．
解析：由圆锥的定义知是两个同底的圆锥形成的组合体．
答案：两个同底的圆锥组合体
7．观察下列四个几何体，其中可看作是由两个棱柱拼接而成的是________(填序号)．
解析：①可看作由一个四棱柱和一个三棱柱组合而成，④可看作由两个四棱柱组合而成．
答案：①④
8．一个圆锥的母线长为20，母线与轴的夹角为60°，则圆锥的高为________．
解析：h＝20cs 60°＝10.
答案：10
9．指出如图(1)(2)所示的图形是由哪些简单几何体构成的．
解：分割原图，使它的每一部分都是简单几何体．
图(1)是由一个三棱柱和一个四棱柱拼接而成的简单组合体．
图(2)是由一个圆锥和一个四棱柱拼接而成的简单组合体．
10．用一个平行于圆锥底面的平面截这个圆锥，截得的圆台上、下底面的面积之比为1∶16，截去的圆锥的母线长是3 cm，求圆台的母线长．
解：设圆台的母线长为l cm，截得圆台的上底面的半径为r cm.
根据题意，得圆台的下底面的半径为4r cm.
根据相似三角形的性质，得eq \f(3,3＋l)＝eq \f(r,4r).解得l＝9.
所以圆台的母线长为9 cm.
B级——面向全国卷高考高分练
1.如图所示的平面中阴影部分绕中间轴旋转一周，形成的几何体形状为( )
A．一个球体
B．一个球体中间挖出一个圆柱
C．一个圆柱
D．一个球体中间挖去一个长方体
解析：选B 圆旋转一周形成球，圆中的矩形旋转一周形成一个圆柱．故选B.
2．[多选]下列说法正确的是( )
A．由若干个平面多边形围成的几何体，称做多面体
B．一条平面曲线绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面
C．旋转体的截面图形都是圆
D．圆锥的侧面展开图是一个扇形
解析：选ABD A、B为定义，均正确；C错误，因为轴截面截圆柱、圆锥、圆台所得截图形分别是矩形、等腰三角形、等腰梯形；D沿母线剪开后，侧面在平面上的展开图是一个扇形，此说法正确．故选A、B、D.
3．用一张长为8，宽为4的矩形硬纸卷成圆柱的侧面，则相应圆柱的底面半径是( )
A．2 B．2π
C.eq \f(2,π)或eq \f(4,π) D.eq \f(π,2)或eq \f(π,4)
解析：选C 如图所示，设底面半径为r，若矩形的长8恰好为卷成圆柱底面的周长，则2πr＝8，所以r＝eq \f(4,π)；同理，若矩形的宽4恰好为卷成圆柱的底面周长，则2πr＝4，所以r＝eq \f(2,π).故选C.
4．已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧，且距离为1，那么这个球的半径是( )
A．4 B．3
C．2 D．0.5
解析：选B 如图所示，∵两个平行截面的面积分别为5π，8π，∴两个截面圆的半径分别为r1＝eq \r(5)，r2＝2eq \r(2).
∵球心到两个截面的距离d1＝ eq \r(R2－r\\al(2,1))，d2＝ eq \r(R2－r\\al(2,2))，
∴d1－d2＝ eq \r(R2－5)－eq \r(R2－8)＝1，∴R2＝9，∴R＝3.故选B.
5．用一个平面去截几何体，如果截面是三角形，那么这个几何体可能是下面哪几种：________(填序号)．
①棱柱；②棱锥；③棱台；④圆柱；⑤圆锥；⑥圆台；⑦球．
解析：可能是棱柱、棱锥、棱台与圆锥．
答案：①②③⑤
6．一个正方体内接于一个球，过球心作一个截面，则在图中，可能是截面的是________．
解析：在组合体内取截面时，要注意交点是否在截面上，如：当截面过对角面时，得(2)；当截面平行正方体的其中一个侧面时，得(3)；当截面不平行于任一侧面且不过对角面时，得(1)，只要是过球心就不可能截出(4)．
答案：(1)(2)(3)
7．一个圆台的母线长为12 cm，两底面面积分别为4π cm2和25π cm2.求：
(1)圆台的高；
(2)截得此圆台的圆锥的母线长．
解：如图，将圆台恢复成圆锥后作其轴截面，设圆台的高为h cm，截得该圆台的圆锥的母线为x cm，由条件可得圆台上底半径r′＝2 cm，下底半径r＝5 cm.
(1)由勾股定理得h＝ eq \r(122－5－22)＝3eq \r(15)(cm)．
(2)由三角形相似得：eq \f(x－12,x)＝eq \f(2,5)，解得x＝20(cm)．
答：(1)圆台的高为3eq \r(15) cm；(2)截得此圆台的圆锥的母线长为20 cm.
C级——拓展探索性题目应用练
如右图所示，圆台母线AB长为20 cm，上、下底面半径分别为5 cm和10 cm，从母线AB的中点M拉一条绳子绕圆台侧面转到B点，求这条绳子长度的最小值．
解析：如右图所示，作出圆台的侧面展开图及其所在的圆锥．连接MB′，在圆台的轴截面中，
∵Rt△OPA∽Rt△OQB，
∴eq \f(OA,OA＋AB)＝eq \f(PA,QB)，∴eq \f(OA,OA＋AB)＝eq \f(5,10).∴OA＝20(cm)．
设∠BOB′＝α，由扇形弧eq \x\t(BB)′的长与底面圆Q的周长相等，得2×10×π＝2×OB×
π×eq \f(α,360°)，
即20π＝2×(20＋20)π×eq \f(α,360°)，
∴α＝90°.
∴在Rt△B′OM中，
B′M＝ eq \r(OM2＋OB′2)＝ eq \r(302＋402)＝50(cm)．
即所求绳长的最小值为50 cm.