人教版九年级上册22.1.4 二次函数y=ax2+bx+c的图象和性质教案
展开1.会画二次函数y=ax2的图象;2.理解并掌握二次函数y=ax2的性质(开口方向、对称轴、顶点、最值、增减性、对称性);3.理解并掌握二次项系数a的作用.
1.画函数图象的方法和步骤?
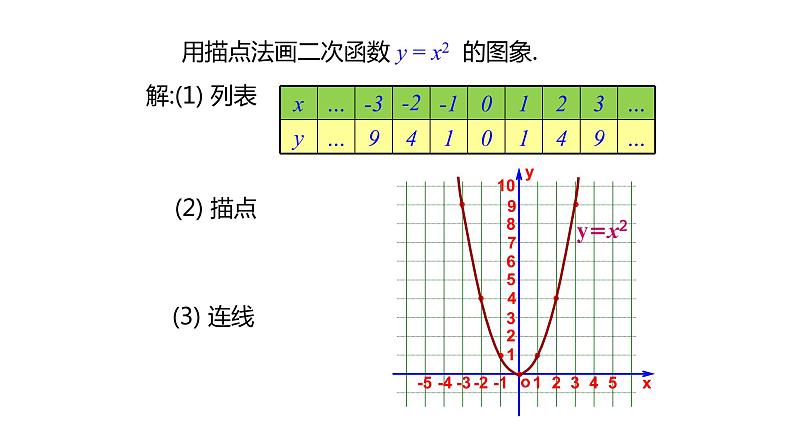
列表:注意自变量的取值范围;描点:先建系,根据表格确定点的坐标;连线:用光滑的曲线连接.
步骤:列表——描点——连线
2.正比例函数的图象和性质?一次函数?
正比例函数 y=kx(k≠0)
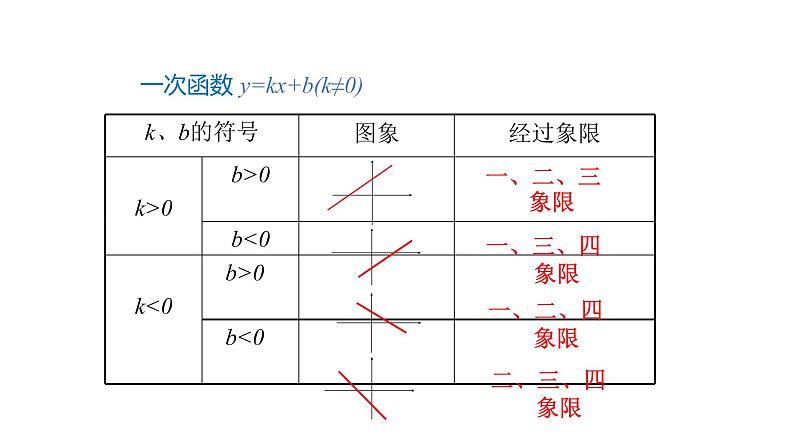
一次函数 y=kx+b(k≠0)
用描点法画二次函数 y = x2 的图象.
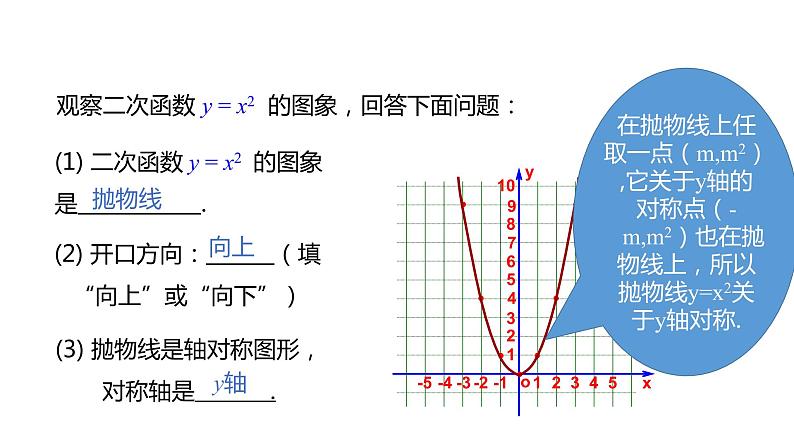
(2) 开口方向: (填“向上”或“向下”)
(1) 二次函数 y = x2 的图象是 .
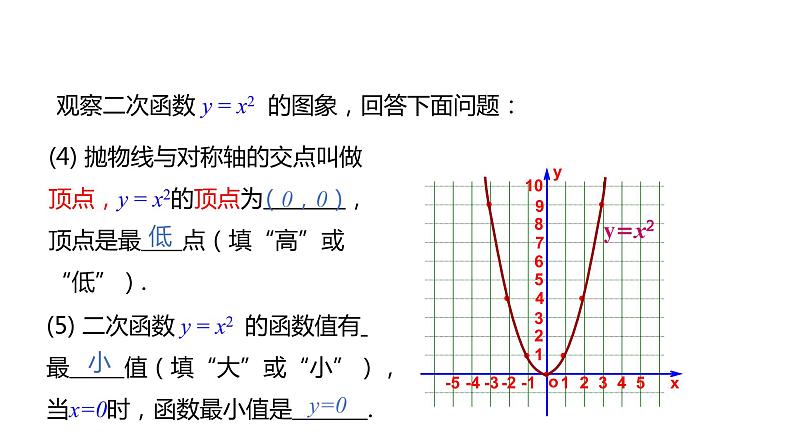
观察二次函数 y = x2 的图象,回答下面问题:
(3) 抛物线是轴对称图形,对称轴是 .
在抛物线上任取一点(m,m2),它关于y轴的对称点(-m,m2)也在抛物线上,所以抛物线y=x2关于y轴对称.
(5) 二次函数 y = x2 的函数值有 最 值(填“大”或“小”),当x=0时,函数最小值是 .
(4) 抛物线与对称轴的交点叫做顶点,y = x2的顶点为 , 顶点是最 点(填“高”或“低”).
(6) 在对称轴y轴的左侧,y随x的增大而 , 在y轴的右侧,y随x的增大而 (填“增大”或“减小”).
以上(2)—(6)是函数 y = x2的性质
相同点:图象都是抛物线,开口方向、对称轴、顶点、最小值、增减性、对称性都相同;不同点:解析式中的a值不同,图象的开口大小不同.
小结:a>0,a越大,抛物线的开口越小.
小结:a>0时,二次函数y=ax2的图象和性质:图象都是抛物线,性质:(1)开口方向:开口向上; (2)开口大小:a越大,抛物线的开口越小; (3)轴对称图形,对称轴为y轴; (4)顶点(0,0); (5)当x=0时,二次函数的函数值有最小值为y=0; (6)增减性:在对称轴y轴左侧,y随x的增大而减小,在对称轴y轴右侧,y随x的增大而增大.
图象都是抛物线,性质:(1)开口向下;. (2)对称轴为y轴; (3)顶点(0,0); (4)函数值有最大值; (5)增减性:在对称轴y轴左侧,y随x的增大而增大,在y轴右侧,y随x的增大而减小.
不同点:解析式中的a值不同,图象的开口大小不同.
小结:a<0,|a|越大,抛物线的开口越小.
当x<0时,y随着x的增大而减小.当x>0时,y随着x的增大而增大.
当x<0时,y随着x的增大而增大.当x>0时,y随着x的增大而减小.
x=0时 , y最小=0
抛物线y=ax2 (a≠0)的形状是由|a|来确定的, |a|越大,开口越小.
对比抛物线,y=x2和y= -x2.它们关于x轴对称吗?一般地,抛物线y=ax2和y=-ax2呢?
判断两点函数值大小的方法:若两点在对称轴同侧,根据增减性判断函数值大小;若两点在对称轴两侧,根据点与对称轴的水平距离判断大小.(a>0,开口向上,距离越大,函数值越大;a<0,开口向下,距离越大,函数值越小) ;除此之外,还可以运用图象法或特殊值法.
5. 已知函数 是二次函数, 且开口向上.(1)求m的值;(2)求出二次函数的解析式?(3)写出此函数的增减性?
(3)此函数的对称轴为y轴,
在y轴左侧,y随x增大而减小;在y轴右侧,y随x增大而增大.
y=ax2的图象和性质
初中人教版22.1.2 二次函数y=ax2的图象和性质教案及反思: 这是一份初中人教版22.1.2 二次函数y=ax2的图象和性质教案及反思,共4页。教案主要包含了情境导入,初步认识,思考探究,获取新知,运用新知,深化理解,师生互动,课堂小结等内容,欢迎下载使用。
初中数学人教版九年级上册22.1.1 二次函数教学设计: 这是一份初中数学人教版九年级上册22.1.1 二次函数教学设计,共2页。教案主要包含了提出问题,范例,做一做,归纳,课堂练习,作业等内容,欢迎下载使用。
人教版九年级上册22.1.1 二次函数教学设计: 这是一份人教版九年级上册22.1.1 二次函数教学设计,共3页。教案主要包含了情境导入,合作探究,板书设计等内容,欢迎下载使用。