高中数学人教B版 (2019)必修 第三册第七章 三角函数7.1 任意角的概念与弧度制7.1.1 角的推广优秀课件ppt

这是一份高中数学人教B版 (2019)必修 第三册第七章 三角函数7.1 任意角的概念与弧度制7.1.1 角的推广优秀课件ppt，文件包含711角的推广课件1-人教B版高中数学必修第三册共26张PPTpptx、711角的推广导学案1-人教B版高中数学必修第三册docx、711角的推广教学设计1-人教B版高中数学必修第三册docx等3份课件配套教学资源，其中PPT共26页， 欢迎下载使用。

问题1：角的概念的推广
引入：初中是怎么定义角的？
（1）我们把有公共端点的两条射线组成的图形称为角，这个公共端点称为角的顶点，这两条射线称为角的边。
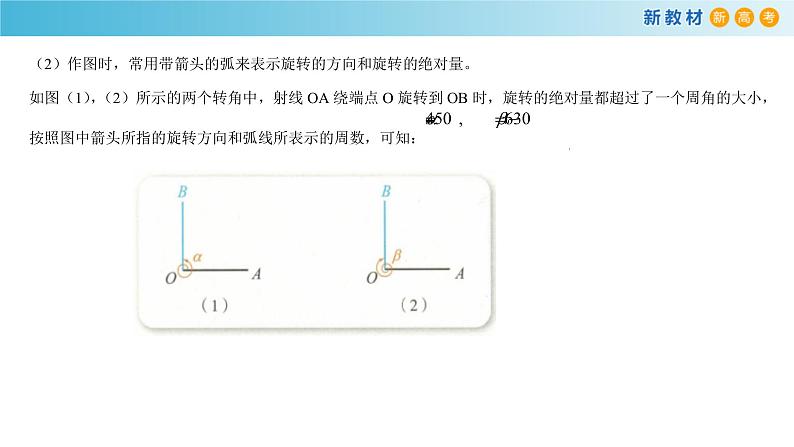
（2）角可以看成是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形。
知识点1　角的概念的推广
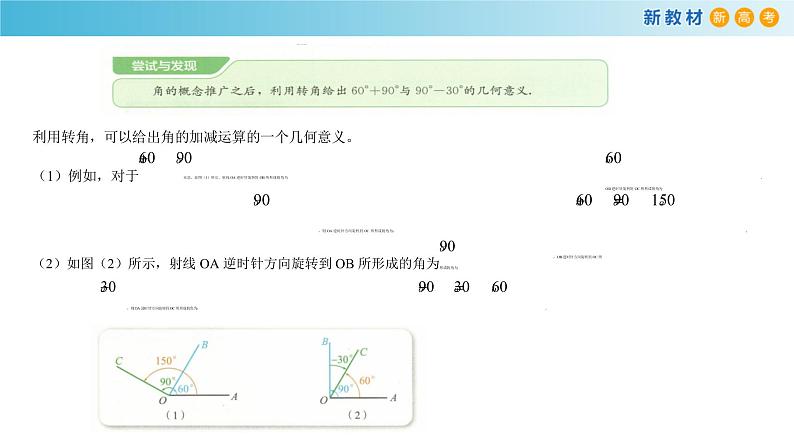
知识点2：角的加减法运算
【对点快练】1．下列说法正确的是(　　)A．最大角是180°　　　　B．最大角是360°C．角不可以是负的　　 D．角可以任意大小
答案：D　由角的定义，角可以是任意大小的．
2．喜洋洋步行从家里到草原学校去上学，一般需要10分钟，则10分钟时间，钟表的分针走过的角度是(　　)A．30°　　B．－30°　　C．60°　　 D．－60°
答案：D　利用定义，分针是顺时针走的，形成的角度是负角，又因为周角为360°，所以有×2＝60°，即分针走过的角度是－60°.
为了方便起见，通常讲角放在平面直角坐标系中来讨论：
角的顶点与坐标原点重合，角的始边落在x轴的正半轴上，角的终边在第几象限，就把这个角称为第几象限角，如果终边在坐标轴上，就认为这个角不属于任何象限．
【对点快练】1．下列哪个角是第三象限角(　　)A．15°　　B．105°　　C．215°　　D．315°
答案：C　∵215°＝180°＋35°，∴215°是第三象限的角．
2．以下说法，其中正确的有(　　)①－75°是第四象限角　　　　　②225°是第三象限角③475°是第二象限角　　　　 ④－315°是第一象限角A．1个　　B．2个　　C．3个　　 D．4个
知识点4　终边相同的角
一般地，角α＋k·360°(k∈Z)与角α的终边相同．任意两个终边相同的角，它们的差一定是360°的整数倍，因此，所有与α终边相同的角组成一个集合，记为S＝{β|β＝α＋k·360°，k∈Z}.
【对点快练】1．下列各角中，与60°角终边相同的角是(　　)A．－300°　　B．－60°　　C．600°　　D．1 380°
答案：A　与60°角终边相同的角α＝k·360°＋60°，k∈Z，令k＝－1，则α＝－300°.
答案：1 110°　3×360°＋30°＝1 110°.
答案：①②③④　①－330°角是第一象限角，但它是负角，所以①不正确．②120°角是第二象限角，390°角是第一象限角，显然390°>120°，所以②不正确．③480°角是第二象限角，但它不是钝角，所以③不正确④0°角是小于180°角，但它既不是钝角，也不是直角或锐角，故④不正确．
【变式练习】已知角α＝2 010°.(1)把α改写成k·360°＋β(k∈Z,0°≤β<360°)的形式，并指出它是第几象限角；(2)求θ，使θ与α终边相同，且－360°≤θ<720°.
解　(1)由2 010°除以360°，得商为5，余数为210°.∴取k＝5，β＝210°，α＝5×360°＋210°.又β＝210°是第三象限角，∴α为第三象限角．(2)与2 010°终边相同的角：k·360°＋2 010°(k∈Z)．令－360°≤k·360°＋2 010°<720°(k∈Z)，解得－6≤k<－3(k∈Z)．所以k＝－6，－5，－4.将k的值代入k·360°＋2 010°中，得角θ的值为－150°，210°，570°.
例3.写出终边在第一象限内的角的集合
【变式练习】已知，如图所示． (1)分别写出终边落在OA，OB位置上的角的集合；(2)写出终边落在阴影部分(包括边界)的角的集合．
解　(1)终边落在OA位置上的角的集合为{α|α＝90°＋45°＋k·360°，k∈Z}＝{α|α＝135°＋k·360°，k∈Z}，终边落在OB位置上的角的集合为{β|β＝－30°＋k·360°，k∈Z}．(2)由图可知，阴影部分角的集合是由所有介于(注：区间内部是实数，严格意义上，角度不能用区间表示．)30°～135°之间的所有与之终边相同的角组成的集合，故该区域可表示为{α|－30°＋k·360°≤α≤135°＋k·360°，k∈Z}．
例4.写出终边在x轴上的角的集合
【变式练习】如图所示，则终边在图中所示直线的角的集合为____________．
答案：{β|β＝135°＋k·180°，k∈Z}　由题图易知，在0°～360°范围，终边在直线y＝－x上的角有两个，即135°和315°，因此，终边在直线y＝－x上的角的集合S＝{β|β＝135°＋k·360°，k∈Z}∪{β|β＝315°＋k·360°，k∈Z}＝{β|β＝135°＋k·180°，k∈Z}．
例5. 已知α为第三象限角，则是第几象限角？
【变式练习】已知α角是第三象限角，则2α是第几象限角？