2021学年第八章 向量的数量积与三角恒等变换8.1 向量的数量积8.1.2 向量数量积的运算律评优课课件ppt

这是一份2021学年第八章 向量的数量积与三角恒等变换8.1 向量的数量积8.1.2 向量数量积的运算律评优课课件ppt，文件包含812向量数量积的运算律课件1-人教B版高中数学必修第三册共22张PPTpptx、812向量数量积的运算律导学案1-人教B版高中数学必修第三册docx、812向量数量积的运算律教学设计1-人教B版高中数学必修第三册docx等3份课件配套教学资源，其中PPT共22页， 欢迎下载使用。
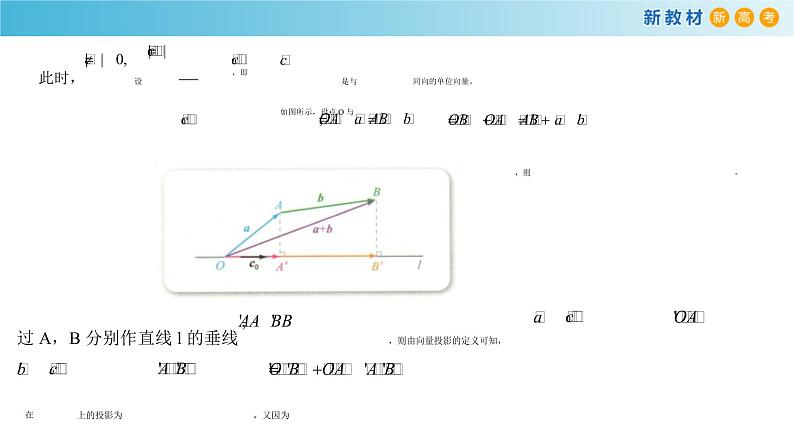
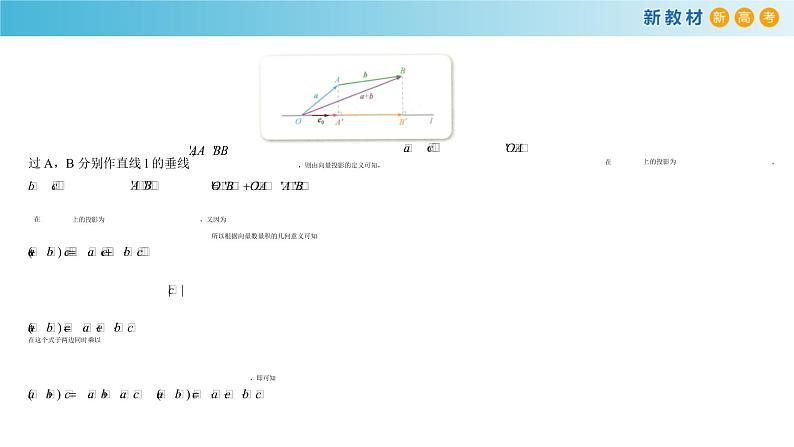
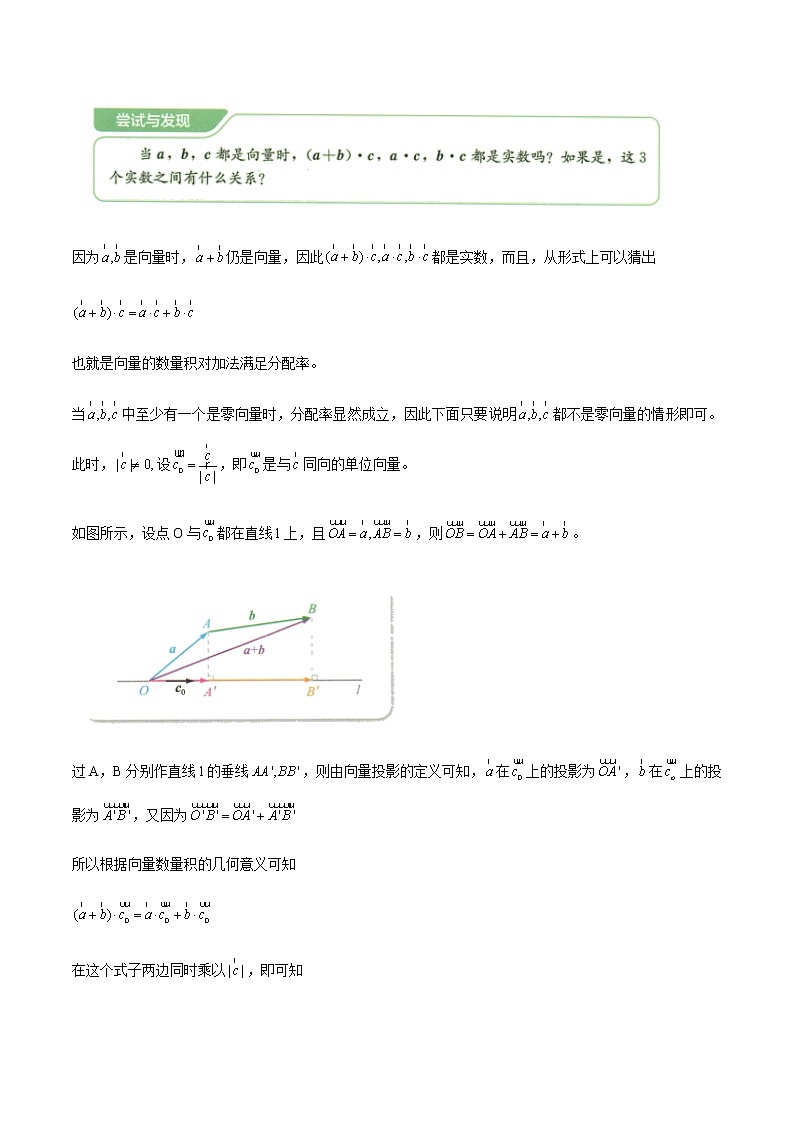
8.1.2 向量数量积的运算律本节课是人教B版必修3第八章的第二课时，上节课学习了向量的数量积的定义及基本性质，并做了简单的运算。学生对运算的意义的理解，通过集合运算、向量的加法、减法、数乘运算，已突破了算术运算的框架。学生在形式上已接受了数量积的定义，但还是向学生说明，之所以定义这种运算，是因为它具有一套优良的运算律。认真证明分配律，解释分配律的几何意义，为用分配律解集合题打下坚实的基础。本节课通过经历探究过程，掌握向量数量积的运算律及几何意义，特别是分配律的几何意义，两个向量和的投影等于各向量投影之和；通过向量运算律的探究，会用运算律证明简单的几何问题；通过问题的解决，培养学生观察问题，分析问题和解决问题的实际操作能力，培养学生观察问题，分析问题和解决问题的实际操作能力，培养学生的交流意识，合作精神，培养学生叙述表达自己解题思路和探索问题的能力。考点教学目标核心素养数量积的运算律掌握数量积的运算律及几何意义，利用数量积求模、求夹角数学抽象、逻辑推理、数学运算数量积的应用利用向量数量积判断两个向量的垂直关系以及其他相关应用问题逻辑推理、数学运算【教学重点】掌握数量积的运算律及几何意义，利用数量积求模、求夹角，利用向量数量积判断两个向量的垂直关系以及其他相关应用问题【教学难点】数量积的运算律的几何意义，数量积的应用引入：当是两个非零向量时，因为，所以根据，可知，即向量的数量积满足交换律。当是实数且是向量时，是向量，与都是实数，那么这两个实数相等吗？事实上，当都是非零向量且时，（1）如果，则，且的方向与的方向相同，从而，因此：（2）如果，则，且的方向与的方向相反，从而，因此：当中至少有一个是零向量或时，显然有用同样的方法可以得到.因为是向量时，仍是向量，因此都是实数，而且，从形式上可以猜出也就是向量的数量积对加法满足分配率。当中至少有一个是零向量时，分配率显然成立，因此下面只要说明都不是零向量的情形即可。 此时，设，即是与同向的单位向量。如图所示，设点O与都在直线l上，且，则。过A，B分别作直线l的垂线，则由向量投影的定义可知，在上的投影为，在上的投影为，又因为所以根据向量数量积的几何意义可知在这个式子两边同时乘以，即可知由向量数量积满足以上的运算律还可以得到：，新知新学：向量数量积的运算律1．交换律：a·b＝b·a.2．(λa)·b＝λ(a·b)＝a·(λb).3．对加法满足分配律：(a＋b)·c＝a·c＋b·c，推广结论：(a＋b)(a－b)＝a2－b2；(a＋b)2＝a2＋2a·b＋b2.【对点快练】1．设e1和e2是互相垂直的单位向量，且a＝3e1＋2e2，b＝－3e1＋4e2，则a·b等于(　　)A．－2　　 B．－1　　C．1　　　 D．2答案：B　因为|e1|＝|e2|＝1，e1·e2＝0，所以a·b＝(3e1＋2e2)·(－3e1＋4e2)＝－9|e1|2＋8|e2|2＋6e1·e2＝－9×12＋8×12＋6×0＝－1.2．对于任意向量a，b，c，下列命题中正确的是(　　)A．|a·b|＝|a||b|　　 B．|a＋b|＝|a|＋|b|C．(a·b)c＝a(b·c)　　 D．|a|＝答案：D　因为a·b＝|a||b|cos〈a，b〉，所以|a·b|≤|a||b|，所以A错误；根据向量加法的平行四边形法则，|a＋b|≤|a|＋|b|，只有当a，b同向时取“＝”，所以B错误；因为(a·b)c是向量，且与向量c共线，a(b·c)是向量，且与向量a共线，所以C错误；因为a·a＝|a||a|cos 0＝|a|2，所以，|a|＝，所以D正确．例1.求证：（1）；   （2）证明：（1）(2) 类似的，还可以证明。【变式练习】已知|a|＝3，|b|＝4，|c|＝5，向量a，b的夹角是120°，a，c的夹角是45°.求：(1)a·b；(2)(a－2b)·(3a＋b)；(3)a·(a－4b＋c)．解　(1)a·b＝|a||b|cos 120°＝3×4×＝－6.(2)(a－2b)·(3a＋b)＝3a2＋a·b－6a·b－2b2＝3|a|2－5a·b－2|b|2＝3×32－5×3×4×cos 120°－2×42＝25.(3)a·(a－4b＋c)＝a2－4a·b＋a·c＝|a|2－4|a||b|cos 120°＋|a||c|cos 45°＝32－4×3×4×＋×3×5×＝48.例2.（1）已知，求；（2）已知，求。解：（1）由题意可知，所以因此.(2)由题意可知即，因此，因此。【变式练习1】已知向量a与b的夹角为120°，且|a|＝4，|b|＝2，求：(1)|a＋b|；(2)|(a＋b)·(a－2b)|.解　由已知a·b＝|a||b|cos θ＝4×2×cos 120°＝－4，a2＝|a|2＝16，b2＝|b|2＝4.(1)∵|a＋b|2＝(a＋b)2＝a2＋2a·b＋b2＝16＋2×(－4)＋4＝12，∴|a＋b|＝2.(2)∵(a＋b)·(a－2b)＝a2－a·b－2b2＝16－(－4)－2×4＝12，∴|(a＋b)·(a－2b)|＝12. 【变式练习2】若向量a与b的夹角为60°，|b|＝4，且(a＋2b)·(a－3b)＝－72，则a的模为(　　)A．2　　　 B．4　　　C．6　　　 D．12答案：C　∵(a＋2b)·(a－3b)＝a2－a·b－6b2＝|a|2－|a|·|b|cos 60°－6|b|2＝|a|2－2|a|－96＝－72，∴|a|2－2|a|－24＝0，∴|a|＝6 例3. (1)已知两个单位向量a，b的夹角为60°，若(2a＋b)⊥(a＋λb)，则λ＝____________.（2）已知a，b是两个非零向量，同时满足|a|＝|b|＝|a－b|，则b与a＋b的夹角是____________．答案：(1)－　[∵(2a＋b)⊥(a＋λb)，∴(2a＋b)·(a＋λb)＝0，∴2a2＋2λa·b＋a·b＋λb2＝0.∵|a|＝|b|＝1，且a与b的夹角为，∴2＋λ＋＋λ＝0.∴λ＝.](2)30°　[由|a|＝|b|，得|a|2＝|b|2，又由|b|＝|a－b|，得|b|2＝|a|2－2a·b＋|b|2，所以a·b＝|a|2.而|a＋b|2＝|a|2＋2a·b＋|b|2＝3|a|2，所以|a＋b|＝|a|.设b与a＋b的夹角为θ，则cos θ＝＝＝，又0≤θ≤180°，所以θ＝30°.]【变式练习】平面内三个向量a，b，c满足|a|＝|b|＝1，|c|＝，且a＋b＋c＝0，则向量a，b的夹角大小是____________．答案：　设向量a与b夹角为θ，∵a＋b＋c＝0，∴a＋b＝－c，∴(a＋b)2＝(－c)2即a2＋2a·b＋b2＝c2，亦即2＋2cos θ＝3，∴cos θ＝，又∵θ∈[0，π]，∴θ＝. 例4.利用向量证明菱形的两条对角线互相垂直。如图所示，已知是菱形，AC与BD是两条对角线，求证：。证明：由已知可得：，所以：又因为ABCD为菱形，所以，即，因此，从而.例5.利用向量证明三角形的三条高相交于一点。如图所示，已知中，分别为边上的高，而且与相交于点O，连接AO并延长，与BC相交于点D，求证：。证明：因为，所以即因此，    （1）又因为所以即因此，    (2)由（1）-（2）可得：，因此从而，故，即。【变式练习1】如图，在▱ABCD中，＝a，＝b，＝，＝.(1)用a，b表示；(2)若|a|＝1，|b|＝4，∠DAB＝60°，分别求||和·的值．解　(1)＝－＝－＝－＋＝－a＋b.(2)因为|a|＝1，|b|＝4，∠DAB＝60°，所以||2＝2＝|b|2－a·b＋|a|2＝－×1×4×cos 60°＋＝.所以||＝.·＝(a＋b)·＝|a|2＋a·b－|b|2＝＋×1×4×cos 60°－＝－4.【变式练习2】如图所示，在等腰直角三角形ACB中，∠ACB＝90°，CA＝CB，D为BC的中点，E是AB上的一点，且AE＝2EB.求证：AD⊥CE.证明　·＝(＋)·(＋)＝·＝·＝·＝－||2＋||2.因为CA＝CB，所以－||2＋||2＝0，故AD⊥CE. 小结：1．向量数量积的运算律交换律a·b＝b·a对数乘的结合律(λa)·b＝λ(a·b)＝a·(λb)分配律(a＋b)·c＝a·c＋b·c2．数量积对结合律一般不成立，因为(a·b)·c是一个与c共线的向量，而(a·c)·b是一个与b共线的向量，两者一般不同．