
北师大版九年级上册第三章 概率的进一步认识2 用频率估计概率练习
展开3.2《用频率估计概率》习题2
一、解答题
1.已知,投掷一枚均匀的硬币,落地时正面或反面向上的可能性相同.有甲、乙两人做投硬币实验,他们分别投硬币100次,结果“正面向上”的次数为:甲60次、乙40次.
(1)求甲、乙做投硬币实验“正面向上”的频率各是多少?
(2)若甲、乙同时做第101次投硬币实验,求“正面都向上”的概率.
2.小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”,小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
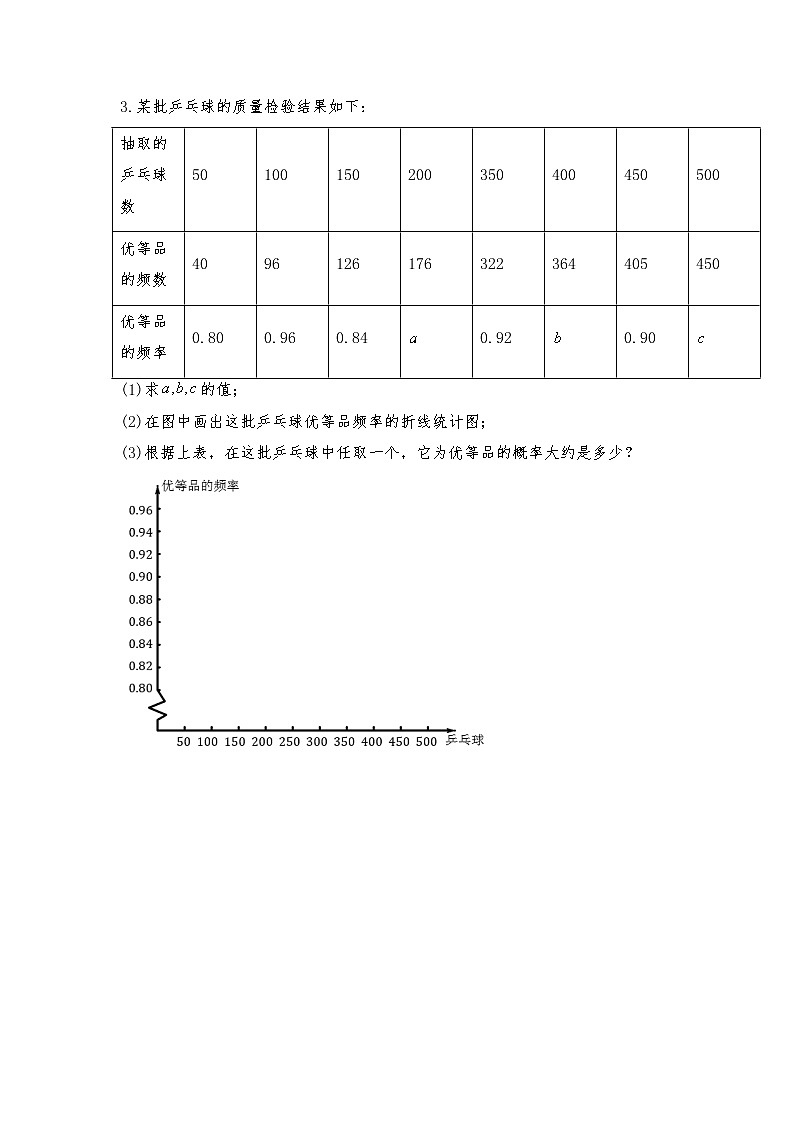
3.某批乒乓球的质量检验结果如下:
抽取的乒乓球数 | 50 | 100 | 150 | 200 | 350 | 400 | 450 | 500 |
优等品的频数 | 40 | 96 | 126 | 176 | 322 | 364 | 405 | 450 |
优等品的频率 | 0.80 | 0.96 | 0.84 | 0.92 | 0.90 |
(1)求的值;
(2)在图中画出这批乒乓球优等品频率的折线统计图;
(3)根据上表,在这批乒乓球中任取一个,它为优等品的概率大约是多少?
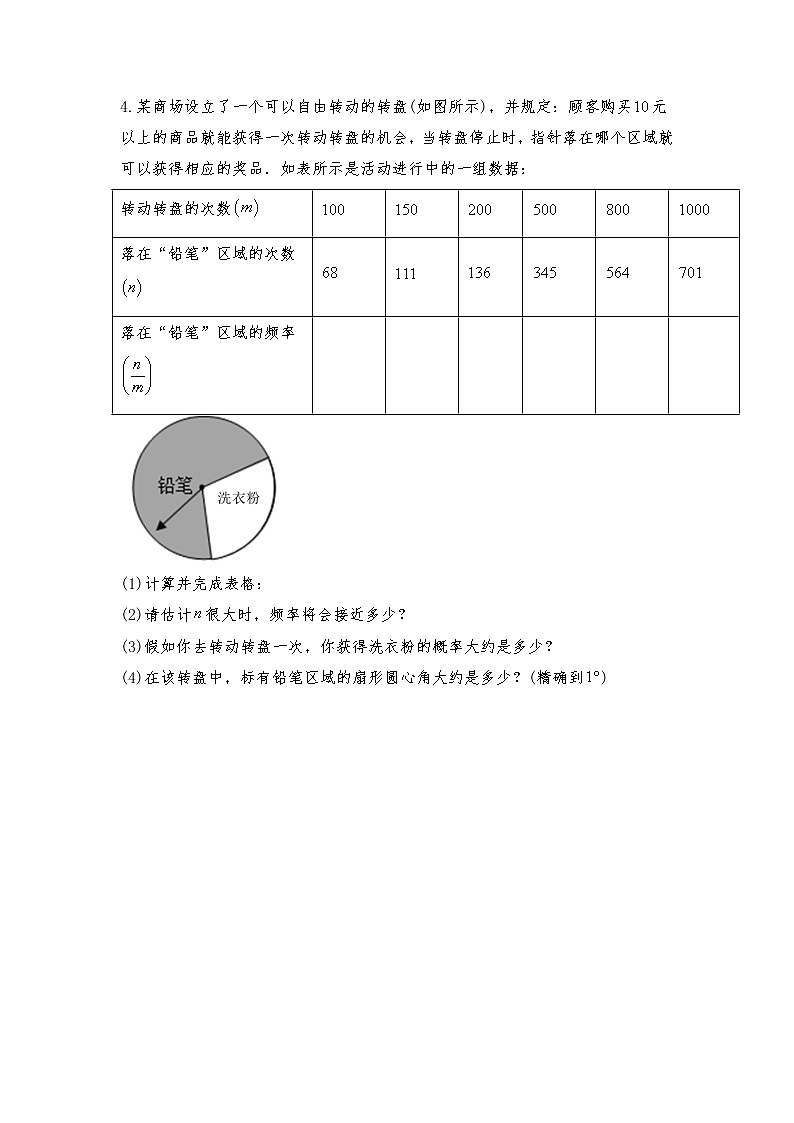
4.某商场设立了一个可以自由转动的转盘(如图所示),并规定:顾客购买元以上的商品就能获得一次转动转盘的机会,当转盘停止时,指针落在哪个区域就可以获得相应的奖品.如表所示是活动进行中的一组数据:
转动转盘的次数 | ||||||
落在“铅笔”区域的次数 | ||||||
落在“铅笔”区域的频率 |
|
|
|
|
|
|
(1)计算并完成表格:
(2)请估计很大时,频率将会接近多少?
(3)假如你去转动转盘一次,你获得洗衣粉的概率大约是多少?
(4)在该转盘中,标有铅笔区域的扇形圆心角大约是多少?(精确到)
5.疫情之后,各大商家为吸引顾客,纷纷采用多种促销手段.其中一个商场设立了一个购物满50元,可以获得一次转动转盘的机会,当转盘停止时,指针落在那个区域就可以得到相应的奖品.下表是活动进行中的一组统计数据:
转动转盘的次数 | 100 | 200 | 500 | 1000 | 1500 | 2000 |
落在“抽纸”的次数 | 51 | 99 | 251 | 502 | 750 | 1002 |
落在“抽纸”的频率 |
|
|
|
|
|
|
(1)完成上表;
(2)请估计,当很大时,频率是多少?
(3)假如你去转动转盘一次,你获得“抽纸”的概率是多少?
6.一粒木质中国象棋子“帅”,它的正面雕刻一个“帅”字,它的反面是平滑的.将它从定高度下掷,落地反弹后可能是“帅”字面朝上,也可能是“帅”字面朝下.由于棋子的两面不均匀,为了估计“帅”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如表:
试验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“帅”字面朝上频数 | a | 18 | 38 | 47 | 52 | 66 | 78 | 88 |
相应频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.55 | 0.56 | b |
(1)表中数据a= ;b= ;
(2)画出“帅”字面朝上的频率分布折线图;
(3)如图实验数据,实验继续进行下去,根据上表的这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?
7.小亮和小丽进行摸球试验.他们在一个不透明的空布袋内,放入两个红球,一个白球和一个黄球,共四个小球.这些小球除颜色外其它都相同.试验规则:先将布袋内的小球摇匀,再从中随机摸出一个小球,记下颜色后放回,称为摸球一次.
(1)小亮随机摸球10次,其中6次摸出的是红球,求这10次中摸出红球的频率;
(2)若小丽随机摸球两次,请利用画树状图或列表的方法,求这两次摸出的球中一个是白球、一个是黄球的概率.
8.王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 |
0.23
|
0.21
|
0.30
|
0.26
|
0.253
|
|
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是 ;(精确到0.01)
(2)估算袋中白球的个数.
9.在一个不透明的盒子里装有红、黑两种颜色的球共40只,这些球除颜色外其余完全相同,为了估计红球和黑球的个数,七(4)班的数学学习小组做了摸球实验.他们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到下表中的一组统计数据:
摸球的次数 | 50 | 100 | 300 | 500 | 800 | 1000 | 2000 |
摸到红球的次数 | 14 | 95 | 155 | 241 | 298 | 602 | |
摸到红球的概率 | 0.28 | 0.33 | 0.317 | 0.31 | 0.301 | 0.301 |
(1)求数据表中 ,
(2)请估计:当次数足够大时,摸到红球的频率将会接近 (精确到0.1)
(3)试估算盒子里红球的数量为 个.
10.在一个不透明的袋子中有1个红球,2个白球和若干个黑球.小明将袋子中的球摇匀后,从中任意摸出一个球,记下颜色后放回袋中并摇匀,在多次重复以上操作后,小明统计了摸到红球的频率,并绘制了如下折线统计图:
(1)袋子中一共有 个球;
(2)若从该袋中同时摸出2个球,求摸出的2个球都是白球的概率.
11.为了能够帮助武汉疫情,某公司通过武汉市慈善总会二维码给武汉捐款,根据捐款情况制成不完整的扇形统计图(图1)、条形统计图(图2).
图1 图2
(1)根据以上信息可知参加捐款总人数为______,______,捐款金额中位数为______,请补全条形统计图;
(2)若从捐款的人中,随机选一人代表公司去其它公司做捐款宣传,求选中捐款不低于元的人的概率;
(3)若其它公司有几人参与了捐款活动,把新捐款数与原捐款数合并成一组新数据,发现众数发生改变,请求出至少有几人参与捐款.
12.随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0x1 | 1x2 | 2x3 | 3x4 | 4x5 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
13.在一个不透明的盒中有m个黑球和1个白球,这些球除颜色外无其他差别.
(1)若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到黑球的频率稳定在0.75左右,则m的值应是_______________;
(2)在(1)的条件下,用m个黑球和1个白球进行摸球游戏.先从盒中随机摸取一个球,再从剩下的球中再随机摸取一个球,求事件“先摸到黑球,再摸到白球”的概率(请用“画树状图”或“列表”等方法写出分析过程).
14.甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下:甲公司规定底薪80元,每销售一件产品提成1元;乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元,
(1)请将两家公司各一名推销员的日工资y(单位:元)分别表示为日销售件数n的函数关系式;
(2)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图、若记甲公司该推销员的日工资为y1,乙公司该推销员的日工资为y2(单位:元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
15.如图,地面上有一个不规则的封闭图形ABCD ,为求得它的面积,小明在此封闭图形内画出一个半径为1 m的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似看成点),记录如下:
(1)当投掷的次数很大时,m:n的值越来越接近_________;
(2)若以小石子所落的有效区域里的次数为总数(即m+n ),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率稳定在_________附近;
(3)如果你掷一次小石子(小石子投进封闭图形ABCD内),那么小石子落在圆内(含圆上)的概率约为_______;
(4)请你利用(2)中所得频率,估计整个封闭图形ABCD的面积是多少平方米(结果保留π).
16.新冠肺炎疫情期间,为了减少外出聚集,“线上购物”受追捧.某电商平台在地区随机抽取了100位居民进行调研,获得了他们每个人近七天“线上购物”消费总金额(单位:元),整理得到如图所示频率统计表.
消费总金额 | 频率 |
0.11 | |
| 0.24 |
|
|
| 0.2 |
| 0.1 |
| 0.04 |
| 0.01 |
(1)求的值,并求从“线上购物”消费总金额不低于500元的被调研居民的概率;
(2)若地区有100万居民,该平台为了促进消费,拟对消费总金额不超过平均水平一半的居民投放每人10元的电子补贴.假设每组中的数据用该组区间的2中点值代替,试根据上述频率统计表,估计该平台在地区拟投放的电子补贴总金额.
17.在不透明箱里放有红、白、黄、蓝四种颜色球共16个,除颜色外都相同,其中白球5个,黄球4个.
(1)小军和小颖为争一个竞赛的名额,决定用摸球的方式来确定,从不透明箱里随机摸出1个球,是白球就小军去,是黄球,就小颖去.请问这个规则是否公平?并通过计算概率说明理由.
(2)现每次从箱中任意摸出一个球记下颜色,再放回箱中,通过大量重复摸球实验后发现,摸到蓝球的频率稳定在25%,那么箱里大约有多少个红球?
答案
一、解答题
1.解:(1)甲的频率=,
乙的频率=.
(2)两人同时投硬币实验一次,结果向上的有正正,正反,反正,反反4种,其中正面都向上的1种,所以P(正面都向上).
2.解:(1)“3点朝上”的频率:6÷60=0.1
“5点朝上”的频率:20÷60=.
(2)小颖的说法是错误的,因为“5点朝上”的频率最大并不能说明5点朝上的概率最大,频率不等于概率;
小红的说法是错误的,因为事件发生具有随机性,故“点朝上”的次数不一定是100次.
(3)列表如下:
共有36种情况,点数之和为3的倍数的情况有12种.
故P(点数之和为3的倍数)==.
3.解:(1),,;
(2)如图所示:
(3)由图知,当抽取的数量逐渐增多时,优等品的频率越稳定在0.9左右,
因此在这批乒乓球中任取一个,它是优等品的概率大约为0.9.
4.解:(1)
故答案为:;;;;;;
(2)由实验可得:当很大时,频率将会接近;
(3)由很大时,获得铅笔的频率将会接近;所以实验获得“洗衣粉”的概率约是;
(4)铅笔区域的扇形的圆心角的度数约为.
5.解:(1)表格中的数据,从左到右依次为51÷100=0.51,99÷200=0.495,251÷500=0.502,502÷1000=0.502,750÷1500=0.5,1002÷2000=0.501.
(2)当转动转盘的次数很大时,指针停止时指向“抽纸”的频率为0.5;
(3)由(2)可知,获得“抽纸”的概率为0.5.
6.(1)a=20×0.7=14;b==0.55;
故答案为:14,0.55;
(2)根据图表给出的数据画折线统计图如下:
(3)随着试验次数的增加“帅”字面朝上的频率逐渐稳定在0.55左右,利用这个频率来估计概率,得P(“帅”字朝上)=0.55.
7.解:(1)小亮随机摸球10次,其中6次摸出的是红球,这10次中摸出红球的频率==;
(2)画树状图得:
∵共有16种等可能的结果,两次摸出的球中一个是白球、一个是黄球的有2种情况,
∴两次摸出的球中一个是白球、一个是黄球的概率==.
8.解:(1)251÷1000=0.251;
∵大量重复试验事件发生的频率逐渐稳定到0.25附近,
∴估计从袋中摸出一个球是黑球的概率是0.25;
(2)设袋中白球为x个,
=0.25,解得x=3.
答:估计袋中有3个白球,
故答案为:(1)0.25;(2)3个.
9.解:(1)a=100×0.33=33,b=298÷1000=0.298;
故答案为:33,0.298;
(2)当次数n足够大时,摸到红球的频率将会接近0.3,
故答案为:0.3;
(3)40×0.3=12(个),
答:盒子里红球的数量为12个;
故答案为:12.
10.解:(1)设袋子中黑球的个数有个,则
将检验x=2是原方程的解
∴1+2+2=5
袋子里一共有个球,
故答案为:
(2)画树状图如下:
所有的等可能的结果有种,其中两次摸到白球的有种,
所有从该袋中同时摸出2个球,摸出的2个球都是白球的概率为:
11.解:(1)捐款总人数为;
捐款为100元人数为所占百分比为,
∴m=32;
本次捐款共50人参加,按捐款数从低到高排序,第25、26个数为150,150,
故中位数为,
补全条形统计图如下:
;
(2);
(3)至少人参与捐款.
原数据众数为元,
若至少增加人,每人捐款元,
则新众数为元和元,
至少增加人.
12.(1)由表中数据,计算所求的概率为P=;
故答案为:;
(2)估计利用该平台点外卖用户的平均送餐距离为:
×(12×0.5+20×1.5+24×2.5+16×3.5+8×4.5)=2.35(千米);
(3)送一份外卖的平均收入为:3×+5+9×=(元),
由150÷≈32.6,
所以估计一天至少要送33份外卖.
13.解:(1):根据题意得=0.75,解得:m=3
经检验:m=3是分式方程的解m=3
故答案为3;
(2)画树状图如下:
从树状图可知,“先从盒子中随机取出一个球,再从剩下的球中再随机摸取一个球”共12种可能的结果,其中“先摸到黑球,再摸到白球”的结果有3种
∴P(先摸到黑球,再摸到白球)=.
14.解:(1)由题意得,甲公司一名推销员的日工资y(单位:元)与销售件数n的关系式为:
y=80+n;
乙公司一名推销员的日工资y(单位:元)与销售件数n的关系式为:y=
即y=;
(2)由频数分布直方图和甲公司日工资的函数关系式得
y1=(80+42)×+(80+44)×+(80+46)×+(80+48)×+(80+50)×
=122×+124×+126×+128×+130×
=125(元)
由频数分布直方和乙公司日工资的函数关系式得
y2=120×+120×+(8×46-240)×+(8×48-240)×+(8×50-240)×
=120×+120×+128×+144×+160×
=136(元),
∴仅从日均收入的角度考虑,选择去乙公司.
15.解:(1)∵
∴m:n的值越来越接近;
(2)观察表格得:随着投随着投掷次数的增大,小石子落在圆内(含圆上)的频率稳定在;
(3)由(1)m:n的值越来越接近可得:m:n=1:2
∴
∴小石子落在圆内(含圆上)的概率约为;
(4)∵
∴
∴
∴封闭图形面积为.
16.解:(1)由,得,
从“线上购物”消费总金额不低于500元的概率为
(2)根据题意,消费总金额平均水平:
(元),
估计不超过平均水平一半的概率为
所以估计投放电子补贴总金额为万元.
17.(1)∵有白球5个,黄球4个,总球数共16个,
∴摸到白球和黄球的概率分别为:P(白球)=,P(黄球)=,
∵>,
∴这个规则不公平;
(2)16×(1---25%)=16×=3(个),
故箱里大约有3个红球.
北师大版九年级下册第三章 圆1 圆课后测评: 这是一份北师大版九年级下册第三章 圆1 圆课后测评,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
北师大版九年级上册2 矩形的性质与判定课后复习题: 这是一份北师大版九年级上册2 矩形的性质与判定课后复习题,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
北师大版九年级上册2 用频率估计概率课后复习题: 这是一份北师大版九年级上册2 用频率估计概率课后复习题,共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













