高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行优质导学案

这是一份高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行优质导学案，共13页。学案主要包含了题组七 面面平行等内容，欢迎下载使用。
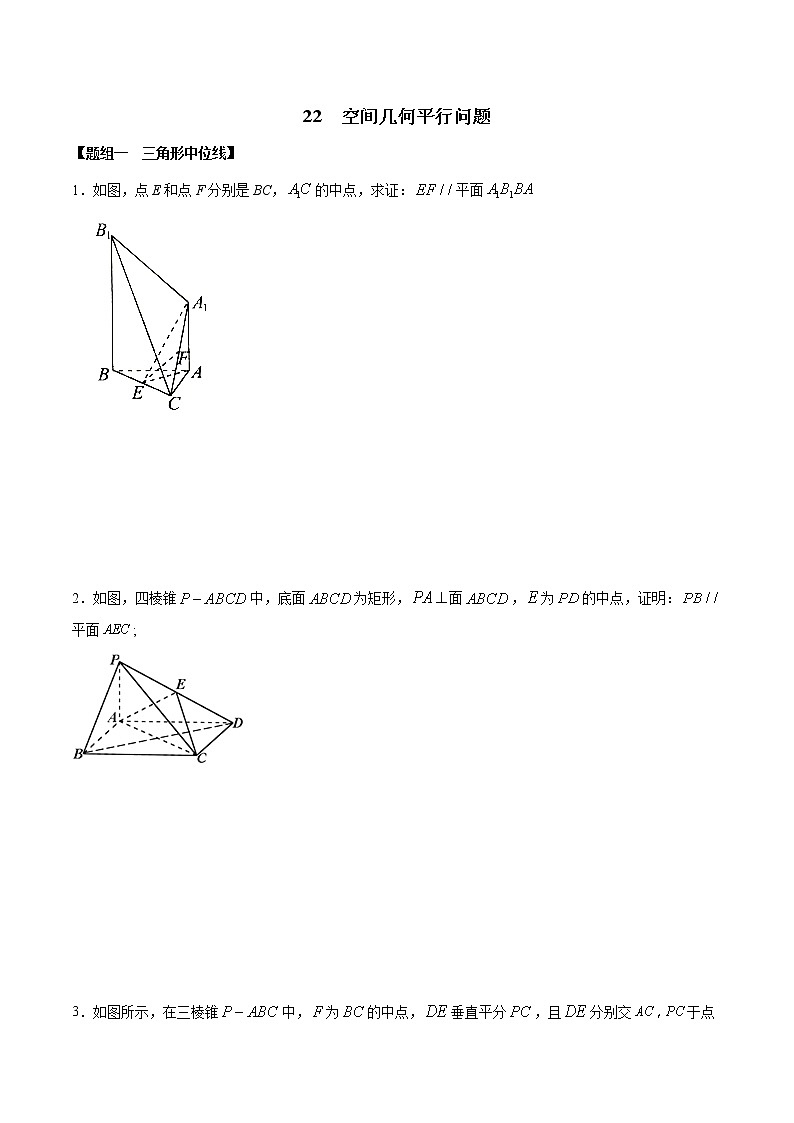
1．如图，点E和点F分别是BC，的中点，求证：平面
2．如图，四棱锥中，底面为矩形，面，为的中点，证明：平面;
3．如图所示，在三棱锥中，为的中点，垂直平分，且分别交于点，证明：
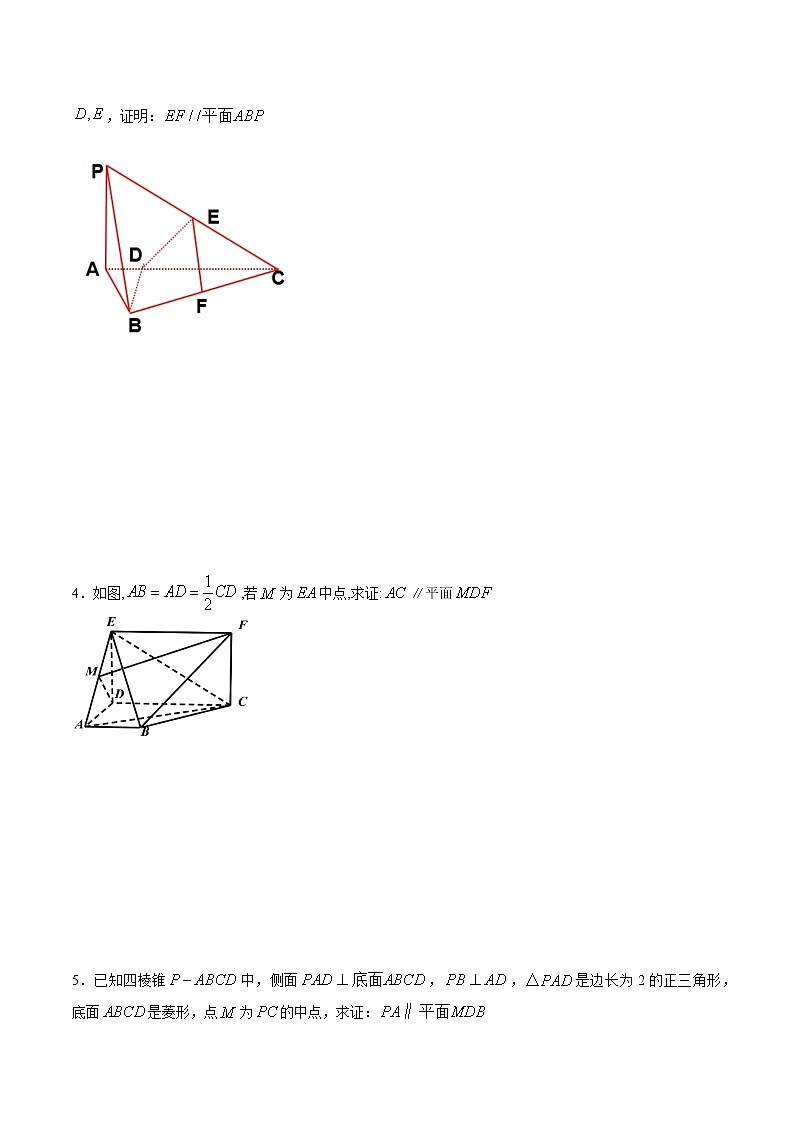
4．如图,,若为中点,求证:∥平面
5．已知四棱锥中，侧面，，是边长为2的正三角形，底面是菱形，点为的中点，求证：
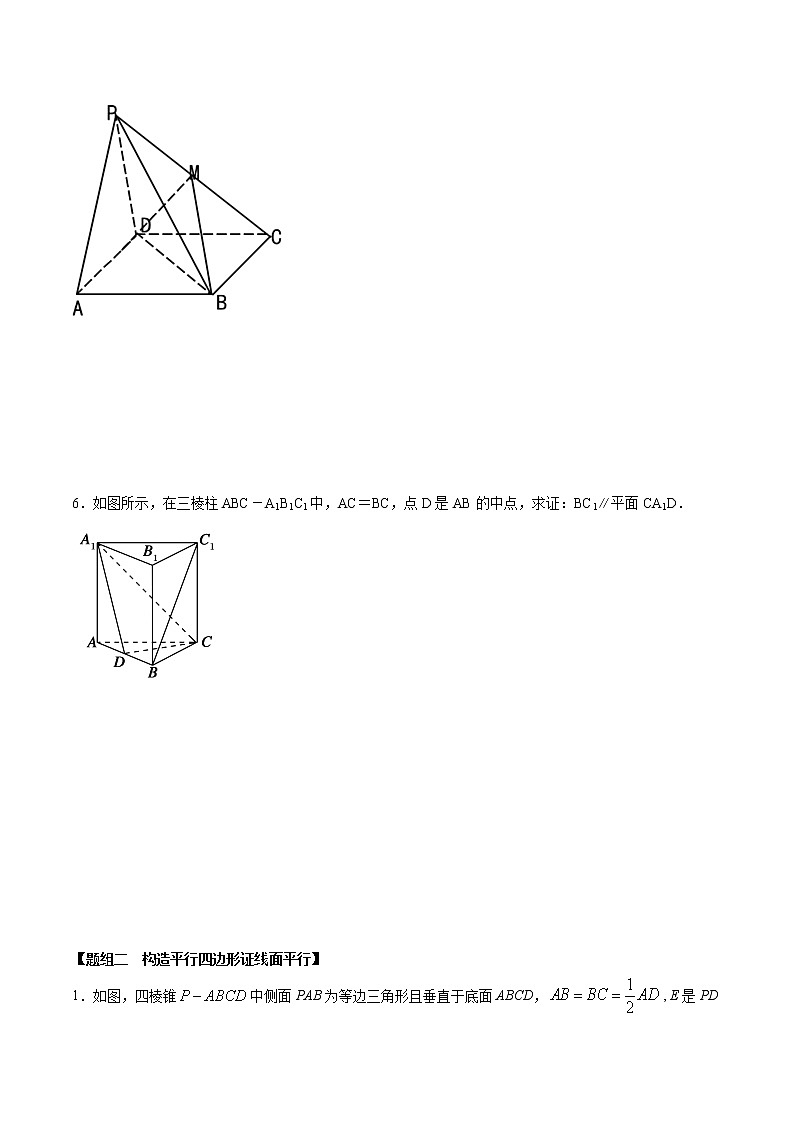
6．如图所示，在三棱柱ABC－A1B1C1中，AC＝BC，点D是AB的中点，求证：BC1∥平面CA1D．
【题组二 构造平行四边形证线面平行】
1．如图，四棱锥中侧面PAB为等边三角形且垂直于底面ABCD，, E是PD的中点，证明：直线∥平面
2．如图，菱形，分别是的中点，求证：平面；
3．由四棱柱截去三棱锥，后得到的几何体如图所示.四边形为正方形，为与的交点，E为的中点，证明：平面
4．在如图所示的五面体中,四边形为菱形,且为中点，求证:平面

【题组三 线面垂直证线面平行】
1．如图所示，在正方体中，是上一点，是的中点，平面.求证：.
2．已知正方体，分别为和上的点，且，.
（1）求证：；
（2）求证：三条直线交于一点.
【题组四 三角形相似比证线线平行】
1．如图，在四面体中，是的中点，是的中点，点在线段上，且求证：平面.
2．如图，三棱锥中，底面ABC，，点E、F分别为PA、AB的中点，点D在PC上，且,明：平面BDE；
【题组五 线面平行性质证线线平行】
1．如图，在三棱柱中，是的中点，是上一点，但平面，则的值为_______.
2.如图，在多面体中，平面，∥，平面平面，，，,求证：∥；
3．如图所示，三棱柱中，点，分别是线段，的中点，设平面与平面的交线为，求证：.
4．如图所示，已知三棱锥中，，分别是边，的中点，过的平面截三棱锥得到的截面为，求证：.
【题组六 面面平行性质证线线平行】
1．在如图所示的五面体中，四边形为平行四边形，平面，，为的中点.求证：平面.
2．如图，在正四棱锥中，点在棱上，且，点为棱的中点,求证：//平面
3．如图，在四棱柱中，底面为梯形，，平面与交于点.
求证：.
4．如图，已知四棱锥的底面为直角梯形，，，底面ABCD，且，M，N分别是PB，PC的中点.求证：平面AMC.
5．如图，在四棱柱中，点M和N分别为和的中点、求证：平面.
【题组七 面面平行】
1．如图，在正方体中，分别是，的中点.
求证：
（1）平面；
（2）平面平面.
2．如图，在三棱柱中，E，F，G分别为，，AB的中点．
求证：平面平面BEF；
若平面，求证：H为BC的中点．