2022版高考数学大一轮复习作业本38《直线、平面平行的判定与性质》(含答案详解)

这是一份2022版高考数学大一轮复习作业本38《直线、平面平行的判定与性质》(含答案详解)，共6页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

一、选择题
在空间四边形ABCD中，E，F分别为AB，AD上的点，且AE：EB=AF：FD=1：4，H，G分别是BC，CD的中点，则( )
A.BD∥平面EFG，且四边形EFGH是平行四边形
B.EF∥平面BCD，且四边形EFGH是梯形
C.HG∥平面ABD，且四边形EFGH是平行四边形
D.EH∥平面ADC，且四边形EFGH是梯形
已知M，N，K分别为正方体ABCD­A1B1C1D1的棱AB，B1C1，DD1的中点，在正方体的所有面对角线和体对角线所在的直线中，与平面MNK平行的直线有( )
A.6条 B.7条 C.8条 D.9条
如图，在长方体ABCD－A′B′C′D′中，下列直线与平面AD′C平行的是( )
A.B′C′ B.A′B C.A′B′ D.BB′
过平面α外的直线l，作一组平面与α相交，如果所得的交线分别为a，b，c，…，那么这些交线的位置关系为( )
A.都平行
B.都相交且一定交于同一点
C.都相交但不一定交于同一点
D.都平行或交于同一点
如图所示，P为矩形ABCD所在平面外一点，矩形对角线交点为O，M为PB的中点，给出下列五个结论：
①PD∥平面AMC；
②OM∥平面PCD；
③OM∥平面PDA；
④OM∥平面PBA；
⑤OM∥平面PBC.
其中不正确的结论的个数有( )
A.1 B.2 C.3 D.4
已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题正确的是( )
A.若m∥α，n∥α，则m∥n
B.若α⊥γ，β⊥γ，则α∥β
C.若m∥α，m∥β，则α∥β
D.若m⊥α，n⊥α，则m∥n
平面α∥平面β的一个充分条件是( )
A.存在一条直线a，a∥α，a∥β
B.存在一条直线a，a⊂α，a∥β
C.存在两条平行直线a，b，a∥α，a∥β，b⊂β
D.存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α
已知α是一个平面，m，n是两条直线，A是一个点，若m⊄α，n⊂α，且A∈m，A∈α，
则m，n的位置关系不可能是( )
A.垂直 B.相交 C.异面 D.平行
已知直线a与直线b平行，直线a与平面α平行，则直线b与α的关系为( )
A.平行
B.相交
C.直线b在平面α内
D.平行或直线b在平面α内
下列说法中，错误的是( )
A.若平面α∥平面β，平面α∩平面γ=l，平面β∩平面γ=m，则l∥m
B.若平面α⊥平面β，平面α∩平面β=l，m⊂α，m⊥l，则m⊥β
C.若直线l⊥平面α，平面α⊥平面β，则l∥β
D.若直线l∥平面α，平面α∩平面β=m，直线l⊂平面β，则l∥m
如图，在棱长为3的正方体ABCD－A1B1C1D1中，E，F，G分别为棱AB，CC1，DD1的中点，过点G作平面D1EF的平行截面，则正方体被截面截得的较小部分的几何体的体积为( )
A.6 B.3 C.eq \f(9,4) D.eq \f(3,2)
如图，在四棱锥P­ABCD中，AB⊥AD，BC∥AD，PA=AD=4，AB=BC=2，PA⊥平面ABCD，点E是线段AB的中点，点F在线段PA上，且EF∥平面PCD，直线PD与平面CEF交于点H，则线段CH的长度为( )
A.eq \r(2) B.2 C.2eq \r(2) D.2eq \r(3)
二、填空题
如图是长方体被一平面所截得的几何体，四边形EFGH为截面，则四边形EFGH的形状为________.
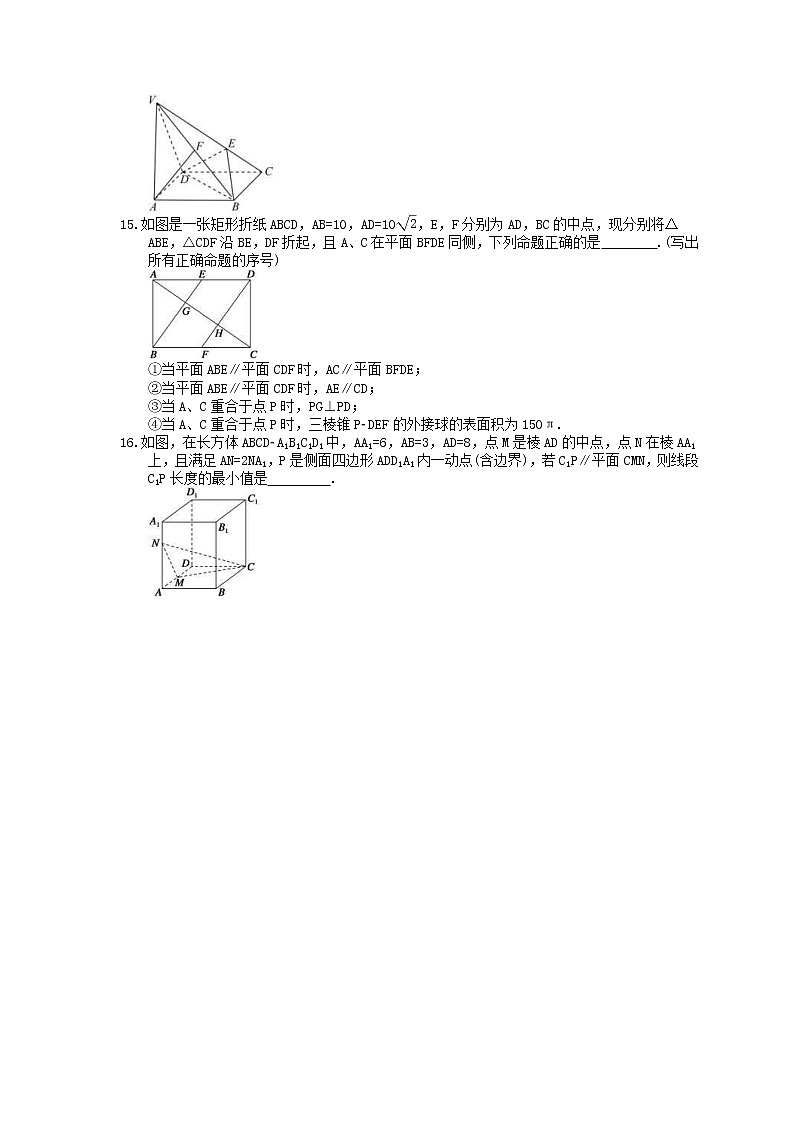
如图，在四棱锥V－ABCD中，底面ABCD为正方形，E，F分别为侧棱VC，VB上的点，
且满足VC=3EC，AF∥平面BDE，则eq \f(VB,FB)=________.
如图是一张矩形折纸ABCD，AB=10，AD=10eq \r(2)，E，F分别为AD，BC的中点，现分别将△ABE，△CDF沿BE，DF折起，且A、C在平面BFDE同侧，下列命题正确的是 .(写出所有正确命题的序号)
①当平面ABE∥平面CDF时，AC∥平面BFDE；
②当平面ABE∥平面CDF时，AE∥CD；
③当A、C重合于点P时，PG⊥PD；
④当A、C重合于点P时，三棱锥P­DEF的外接球的表面积为150π.
如图，在长方体ABCD­A1B1C1D1中，AA1=6，AB=3，AD=8，点M是棱AD的中点，点N在棱AA1上，且满足AN=2NA1，P是侧面四边形ADD1A1内一动点(含边界)，若C1P∥平面CMN，则线段C1P长度的最小值是 .
\s 0 参考答案
答案为：B.
解析：如图，由条件知，EF∥BD，EF=eq \f(1,5)BD，HG∥BD，HG=eq \f(1,2)BD，∴EF∥HG，
且EF=eq \f(2,5)HG，∴四边形EFGH为梯形.
∵EF∥BD，EF⊄平面BCD，BD⊂平面BCD，∴EF∥平面BCD.
∵四边形EFGH为梯形，∴线段EH与FG的延长线交于一点，
∴EH不平行于平面ADC.故选B.
答案为：A.
解析：补形得到平面MNK与正方体侧面的交线，得到正六边形MENFKG，如图所示.
由线面平行的判定定理，可得BD，B1D1，BC1，AD1，AB1，DC1所在直线与平面MNK平行，
∴正方体的所有面对角线和体对角线所在的直线中，与平面MNK平行的有6条.故选A.
答案为：B
解析：连接A′B，∵A′B∥CD′，CD′⊂平面AD′C，
A′B⊄平面AD′C，∴A′B∥平面AD′C.
答案为：D
解析：若l∥平面α，则交线都平行；若l∩平面α=A，则交线都交于同一点A.
答案为：B
解析：矩形ABCD的对角线AC与BD交于点O，所以O为BD的中点.在△PBD中，M是PB的中点，所以OM是△PBD的中位线，OM∥PD，则PD∥平面AMC，OM∥平面PCD，且OM∥平面PDA.因为M∈PB，所以OM与平面PBA、平面PBC相交.
答案为：D.
解析：对于A，若m∥α，n∥α，则m与n可能平行，可能相交，也可能异面，故A错误；对于B，若α⊥γ，β⊥γ，则α与β可能平行，也可能相交(比如直三棱柱相邻两侧面都与底面垂直)，故B错误；对于C，若m∥α，m∥β，则α与β可能平行，也可能相交，故C错误；对于D，垂直于同一平面的两条直线相互平行，故D正确.综上，故选D.
答案为：D.
解析：存在一条直线a，a∥α，a∥β，有可能a平行于两平面的交线，该条件不是平面α∥平面β的一个充分条件，故A错；存在一条直线a，a⊂α，a∥β，有可能a平行于两平面的交线，该条件不是平面α∥平面β的一个充分条件，故B错；存在两条平行直线a，b，a∥α，a∥β，b⊂β，有可能a平行于两平面的交线，该条件不是平面α∥平面β的一个充分条件，故C错；存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α，据此可得平面α∥平面β，该条件是平面α∥平面β的一个充分条件.故选D.
答案为：D.
解析：对于选项A，当m⊥α时，因为n⊂α，所以m⊥n，可能；
对于选项B，当A∈n时，m∩n=A，可能；
对于选项C，若A∉n，由异面直线的定义知m，n异面，可能；
对于选项D，若m∥n，因为m⊄α，n⊂α，所以m∥α，这与m∩α=A矛盾，不可能平行，故选D.
答案为：D.
解析：依题意，直线a必与平面α内的某直线平行，又a∥b，因此直线b与平面α的位置关系是平行或直线b在平面α内.
答案为：C；
解析：对于A，由面面平行的性质定理可知为真命题，故A正确；对于B，由面面垂直的性质定理可知为真命题，故B正确；对于C，若l⊥α，α⊥β，则l∥β或l⊂β，故C错误；对于D，由线面平行的性质定理可知为真命题，故D正确.综上，选C.
答案为：D
解析：如图，连接GC，则GC∥D1F，延长D1F交DC的延长线于M，连接EM，
作CN∥EM交AD于点N，连接GN，
则平面GCN为平行于平面D1EF的截面，正方体被截面截得的较小部分的几何体为
D－GCN，DG=eq \f(3,2)，CD=3，由tan∠DCN=tan∠DME=eq \f(2,3)⇒
DN=CDtan∠DCN=3×eq \f(2,3)=2⇒VD－GCN=VG－CDN=eq \f(1,6)×eq \f(3,2)×3×2=eq \f(3,2).
答案为：C.
解析：∵PD与平面CEF交于点H，
∴平面CEF∩平面PCD=CH，∵EF∥平面PCD，
∴EF∥CH，过点H作HM∥PA交AD于点M，连接CM，
∵EF∩AF=F，CH∩HM=H，∴平面AEF∥平面CHM，
∵平面AEF∩平面ABCD=AE，平面CHM∩平面ABCD=CM，∴AE∥CM，又BC∥AM，
∴四边形ABCM为平行四边形，∴AM=2.又AD=4，
∴M是AD的中点，则H为PD的中点，
∴CH=eq \r(CM2＋MH2)=eq \r(22＋22)=2eq \r(2)，故选C.
答案为：平行四边形
解析：∵平面ABFE∥平面DCGH，又平面EFGH∩平面ABFE=EF，
平面EFGH∩平面DCGH=HG，∴EF∥HG.同理EH∥FG，∴四边形EFGH的形状是平行四边形.
答案为：2
解析：连接AC交BD于点O，连接EO，取VE的中点M，连接AM，MF，
由VC=3EC⇒VM=ME=EC，又AO=CO⇒AM∥EO⇒AM∥平面BDE⇒平面AMF∥平面BDE
⇒MF∥平面BDE⇒MF∥BE⇒VF=FB⇒eq \f(VB,FB)=2.
答案为：①④.
解析：在△ABE中，tan∠ABE=eq \f(\r(2),2)，在△ACD中，tan∠CAD=eq \f(\r(2),2)，
所以∠ABE=∠DAC，由题意，将△ABE，△DCF沿BE，DF折起，且A，C在平面BEDF同侧，此时A、C、G、H四点在同一平面内，平面ABE∩平面AGHC=AG，平面CDF∩平面AGHC=CH，当平面ABE∥平面CDF时，得到AG∥CH，显然AG=CH，所以四边形AGHC为平行四边形，所以AC∥GH，进而可得AC∥平面BFDE，故①正确；
由于折叠后，直线AE与直线CD为异面直线，所以AE与CD不平行，故②不正确；
当A、C重合于点P时，可得PG=eq \f(10\r(3),3)，PD=10，又GD=10，∴PG2＋PD2≠GD2，
所以PG与PD不垂直，故③不正确；
当A，C重合于点P时，在三棱锥P­DEF中，△EFD与△FCD均为直角三角形，
所以DF为外接球的直径，即R=eq \f(DF,2)=eq \f(5\r(6),2)，
所以外接球的表面积为S=4πR2=4π×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5\r(6),2)))2=150π，故④正确.
综上，正确命题的序号为①④.
答案为：eq \r(17).
解析：取A1D1的中点Q，过点Q在平面ADD1A1内作MN的平行线交DD1于点E，
易知平面C1QE∥平面CMN，在△C1QE中作C1P⊥QE，此时C1P取得最小值eq \r(17).