2019-2020学年四川省成都市金牛区成都市十八中学校九上期中数学试卷

这是一份2019-2020学年四川省成都市金牛区成都市十八中学校九上期中数学试卷，共19页。试卷主要包含了4×105 C． 6，14−π0+−12−1．，4，cs25∘≈0， 【答案】C， 【答案】D， 【答案】A， 【答案】B等内容，欢迎下载使用。
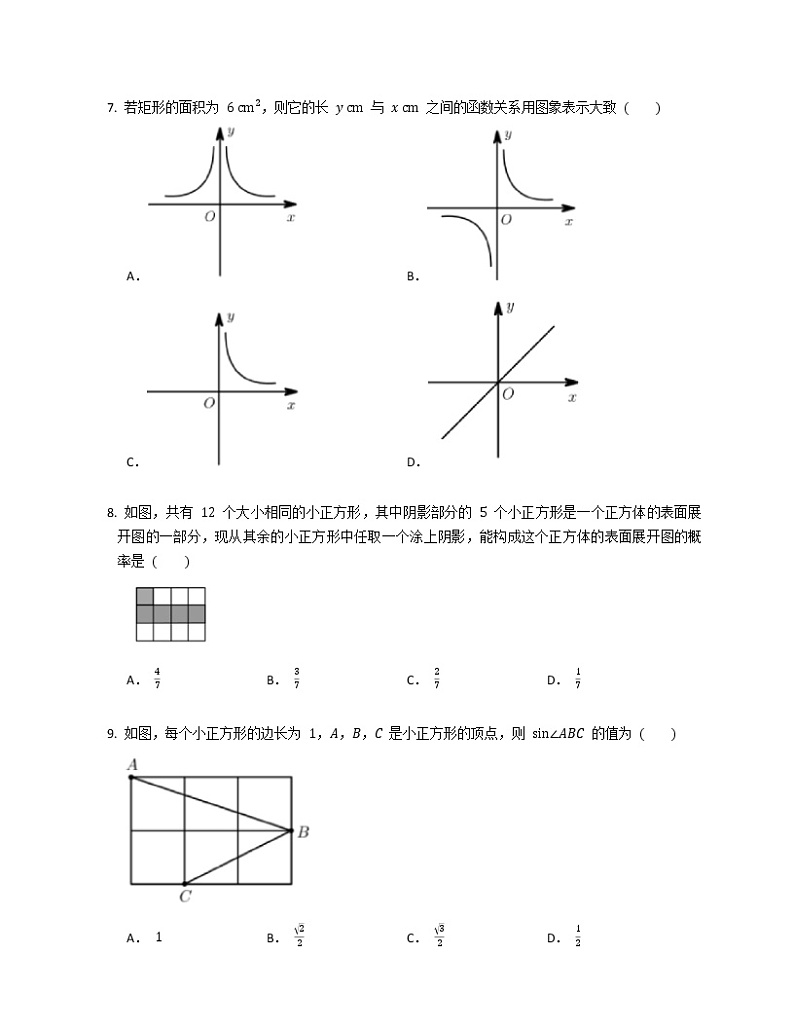
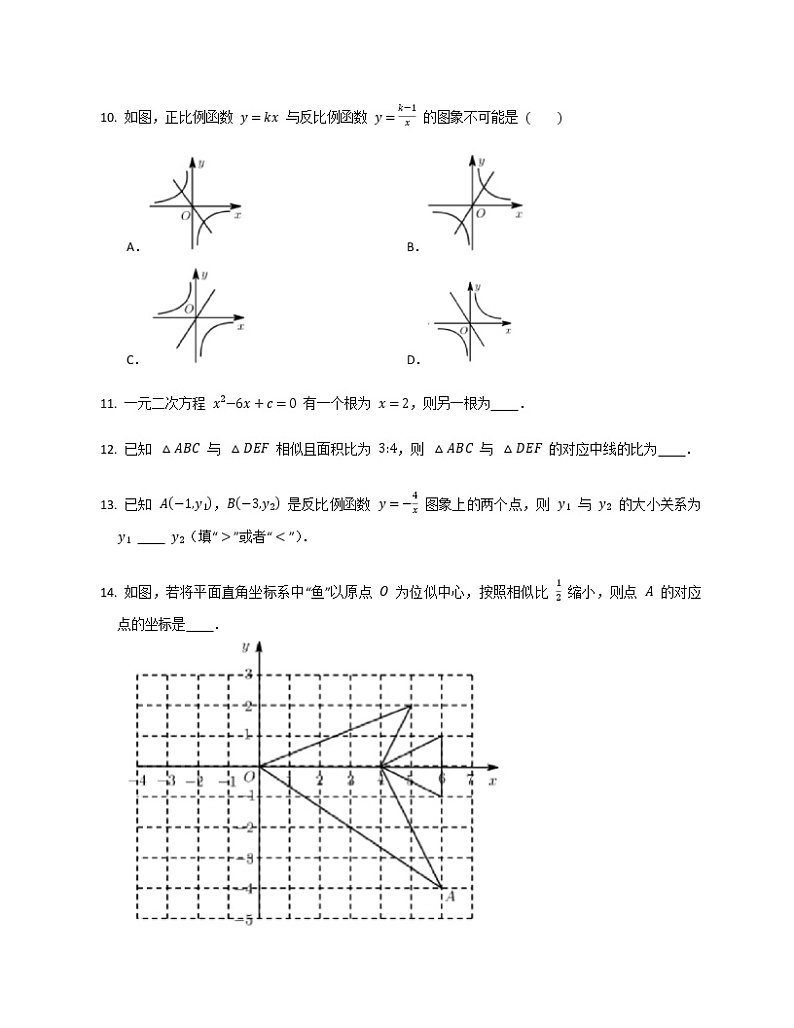
2019-2020学年四川省成都市金牛区成都市十八中学校九上期中数学试卷已知 是一元二次方程 的一根，则 的值为  A．  B．  C．  D．  点 在反比例函数 的图象上，则 的值为  A．  B．  C．  D．  如图，几何体上半部为正三棱柱，下半部为圆柱，其俯视图是  A． B． C． D． 某世博会开园第一个月共售出门票 万张， 万用科学计数法表示为  A．  B．  C．  D．  若分式 的值为 ，则  A．  B．  C．  D．  如图，在平行四边形 中，，点 ， 分别是 ， 的中点，则 等于  A．  B．  C．  D．  若矩形的面积为 ，则它的长 与 之间的函数关系用图象表示大致  A． B． C． D． 如图，共有 个大小相同的小正方形，其中阴影部分的 个小正方形是一个正方体的表面展开图的一部分，现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表面展开图的概率是  A．  B．  C．  D．  如图，每个小正方形的边长为 ，，， 是小正方形的顶点，则 的值为  A．  B．  C．  D．  如图，正比例函数 与反比例函数 的图象不可能是  A． B． C． D． 一元二次方程 有一个根为 ，则另一根为    ． 已知 与 相似且面积比为 ，则 与 的对应中线的比为    ． 已知 ， 是反比例函数 图象上的两个点，则 与 的大小关系为      （填“”或者“”）． 如图，若将平面直角坐标系中“鱼”以原点 为位似中心，按照相似比 缩小，则点 的对应点的坐标是    ． 完成下列小题．(1)  计算：．(2)  解方程：． 化简求值：，其中 ． 某探测队在地面 ， 两处均探测出建筑物下方 处有生命迹象，已知探测线与地面的夹角分别是 和 ，且 米，求该生命迹象所在位置 的深度．（结果精确到 米，参考数据：，，，） 为了解某中学学生课余生活情况，对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计．现从该校随机抽取 名学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名学生只能选择其中一项）．并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图．由图中提供的信息，解答下列问题．(1)  求 的值；(2)  若该校学生共有 名，试估计该校喜爱看电视的学生人数；(3)  若调查到喜爱体育活动的 名学生中有 名男生和 名女生，现从这 名学生中任意抽取 名学生，求恰好抽到 名男生的概率． 已知，如图，反比例函数 的图象与一次函数 的图象相交于点 ，．(1)  试确定这两个函数的表达式；(2)  求 面积；(3)  直接写出使反比例函数的值大于一次函数的值的 的取值范围． 如图，在 中，， 是中线，．一个以点 为顶点的 角绕点 旋转，使角的两边分别与 ， 的延长线相交，交点分别为点 ，， 与 交于点 ， 与 交于点 ．(1)  如图 ，若 ，求证：；(2)  如图 ，在 绕点 旋转的过程中；  探究三条线段 ，， 之间的数量关系，并说明理由；  若 ，，求 的长． 已知 ，代数式 的值为    ． 已知反比例函数 与一次函数 的交点横坐标分别为 ，，则     ． 已知正方形 ， 为等边三角形，连接 ，则     ． 如图，在函数 的图象上有点 ，，  ，，，点 的横坐标为 ，且后面每个点的横坐标与它前面相邻点的横坐标的差都是 ，过点 ，，  ，， 分别作 轴、 轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分的面积从左至右依次记为 ，，  ，，则     ，     ．（用含 的代数式表示） 如图，矩形 中，，点 ，点 ， 在反比例函数 的图象上， 与 轴的正半轴相交于点 ，若 为 的中点，则 的值为    ． 某电器城经销A型号彩电，今年四月份每台彩电售价为 元．与去年同期相比，结果卖出彩电的数量相同，但去年销售额为 万元，今年销售额只有 万元．(1)  问去年四月份每台A型号彩电售价是多少元．(2)  为了改善经营，电器城决定再经销B型号彩电，已知A型号彩电每台进货价为 元，B型号彩电每台进货价为 元，电器城预计用不多于 万元且不少于 万元的资金购进这两种彩电共 台，问有哪几种进货方案．(3)  电器城准备把A型号彩电继续以原价每台 元的价格出售，B型号彩电以每台 元的价格出售，在这批彩电全部卖出的前提下，如何进货才能使电器城获利最大？最大利润是多少． 正方形 中， 在对角线 上， 在线段 的延长线上（如图），且 ，过点 作 于 ，直线 分别交线段 ， 于 ，， 在线段 上 ，连接 交对角线 于 ．(1)  求证：．(2)  设 ，若 ，，求出 与 的关系式．(3)  点 在线段 的左侧，且 为等腰三角形时，若 ，求 的长． 如图①，点 为坐标原点，点 在 轴的正半轴上，四边形 是平行四边形，，反比函数 在第一象限内的图象经过点 ，与 交于点 ．(1)  若 ，求反比例函数的解析式．(2)  若点 为 的中点，且 的面积为 ，求 的长和点 的坐标．(3)  在（）的条件下，过点 作 ，交 于点 （如图②所示），点 为直线 上的一个动点，连接 ， 是否存在这样的点 ，使以 ，， 为顶点的三角形是直角三角形？若存在，请求出 的坐标；若不存在，请说明理由．
答案1.  【答案】C【解析】将 代入 得 ， ． 2.  【答案】C【解析】将 代入 得：． 3.  【答案】C【解析】圆柱的俯视图为圆，且正三棱柱的俯视图为正三角形． 4.  【答案】C【解析】 ． 5.  【答案】D【解析】由题意可得 且 ，解得 ． 6.  【答案】C【解析】 四边形 是平行四边形， ，  点 ， 分别是 ， 的中点， ． 7.  【答案】C【解析】矩形面积为 ，长为 ，宽为 ，则 ，，图象在第一象限． 8.  【答案】A【解析】取第三排的任何一个都可以概率为 ． 9.  【答案】B【解析】连接 ，则 ，，，  为等腰直角三角形，． 10.  【答案】D【解析】若 时，此时 ，正比例函数图象必定经过一，三象限，当 时，所以反比例函数 必定经过二，四象限，故C的图象有可能，当 时，所以反比例函数 必定经过一，三象限，故B的图象有可能，若 时，此时 ，正比例函数图象必定经过二，四象限，所以反比例函数 必定经过二，四象限，故A的图象有可能． 11.  【答案】  【解析】 的一个根为 ． ，另一个根为 ． 12.  【答案】  【解析】 与 相似且面积比为 ，  相似比为 ，对应中线之比为也为 ． 13.  【答案】  【解析】如图，， 在 的图象上表示为由图可知 ． 14.  【答案】 或  【解析】由图可知 ，以原点 为位似中心，按照相似比为 缩小，同侧时对应点坐标为 ，异侧时坐标为 ． 15.  【答案】(1)    (2)  经检验， 是原方程的解．  16.  【答案】 当 时，． 17.  【答案】作 交 延长线于 ，设 米．  中，，所以 ，所以 ，  中，，由 ，解得：．所以生命迹象所在位置 的深度约为 米． 18.  【答案】(1)   ．(2)  样本中喜爱看电视的人数为 （名）， （名），  估计该校喜爱看电视的学生人数为 名． (3)  画树状图如图所示．共有 种等可能的结果数，其中恰好抽到 名男生的结果数为 ，  恰好抽到 名男生的概率 ．  19.  【答案】(1)    在 图象上， ，  反比例函数解析式为 ，将 ， 代入 ，得 解得   一次函数解析式为 ． (2)  被直线 与 轴交于 点，则 ，  (3)  由图象可得反比例函数值大于一次函数值时 的取值范围为： 或 ． 20.  【答案】(1)    ，，，   ，．   ．在 和 中，     ．   ．(2)  三条线段 ，， 之间的数量为：  .理由如下：   ，   ， 又   ，   ．   ．   ，即 ．   ，，，   ，   ．  如图，过点 作 于点 ，则 ，．当 ， 时，由 ，得 ，  在 中，．   ，，   ．   ，   ．   ． 21.  【答案】  【解析】 ， ， ， ． 22.  【答案】 ．【解析】 反比例函数 与一次函数 的交点横坐标为a，b．  令 ，整理得 ， ， 是方程 的两根． ，． ． 23.  【答案】  【解析】如图，过 点作 交 延长线于点 ，  为等边三角形，四边形 为正方形， ，，，令 ，则 ，，， ． 24.  【答案】；【解析】当 时， 的纵坐标为 ，当 时， 的纵坐标为 ，当 时， 的纵坐标为 ，当 时， 的纵坐标为 ，当 时， 的纵坐标为：，  则 ， ， ，   ． 25.  【答案】【解析】如图，作 轴于 ，过 点作 轴的平行线与过 点垂直与 轴的直线交于 ， 交 轴于 ，作 轴于 ，  四边形 是矩形， ， ， ， ， ， 为 的中点， ，在 和 中，     ，   ，，   ，   ，同理：，，   ，，   ，，   ，   ，解得 ，，   ，   ． 26.  【答案】(1)  设去年四月份每台A型号彩电售价是 元，依题意，得解得经检验 是所列方程的解，即去年四月份每台A型号彩电售价是 元；(2)  设A型号彩电购进 台，则B型号彩电购进 台，购进共需 元，依题意，得解得 为整数，，有四种进货方案：A型号彩电购进 台，B型号彩电购进 台，A型号彩电购进 台，B型号彩电购进 台，A型号彩电购进 台，B型号彩电购进 台，A型号彩电购进 台，B型号彩电购进 台．(3)  设A型号彩电购进 台，则B型号彩电购进 台，则利润 ， ，  当 时，利润最大，最大利润 元，即A型号彩电购进 台，B型号彩电购进 台，电器城获利最大，最大利润为 元． 27.  【答案】(1)  在 上截取 ，连接 ，  四边形 是正方形， ，，  在 和 中：   ， ， ，即 ，又 于点 ， ，又 ，  四边形 是平行四边形， ， ， ． (2)  作 ， ，， ，， ， ， ， ，在等腰 中，，， ， ， ， ， ，． (3)  易证 ， ，  为等腰三角形， ， ，设 ， ，在 中，， ， ， ，  为正方形， ， ， ， ， ，， ．  28.  【答案】(1)   ， ，设 ， ， ， ， ，将 代入 ，得 ，  反比例函数解析式为：．(2)   ，四边形 是平形四边形， 是 中点，设 ，则 ，过 作 轴， 轴分别交 轴于 ， 点， ， ，，，    或 （舍），，，， ，， ．(3)    是直角三角形分三种情况：①当 时，如图 ，过 作 交 于点 ，由（）得 ，， ， ， ，令 ， ， ．②当 时，如图 ，过 作 交 于点 ， ，， ，将 代入 ，得 ， ，令 ， ， ．③当 时，如图 ，过 作 轴交 延长线于 ，则 ， ，，设 坐标为 ，则 ，，， ，解得 ，  在第二象限， ．同理，过 作 轴交于 于点 ，则 ，，设 ，则 ，，， ，解得 （舍）， ，综上， 的坐标为 或 或 或 ．