北师大版八年级上册2 平方根课文内容课件ppt

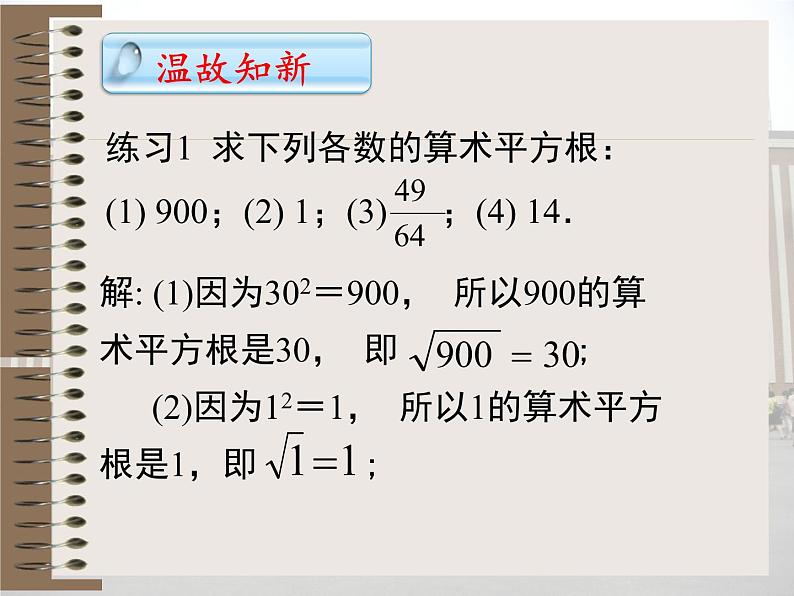
这是一份北师大版八年级上册2 平方根课文内容课件ppt，共46页。PPT课件主要包含了算术平方根，议一议，平方根的性质，记一记，小试牛刀，习题24，教师寄语等内容，欢迎下载使用。
第二章 实数 2.2平方根(2)
北师大版数学八年级上册
1、理解数的平方根的概念，能运用根号表示一个数的平方根； 2、能正确区分平方根与算术平方根的意义； 3、掌握用平方根运算求某些数的平方根的方法。
（1）像0.585885888588885…，1.41421356…，－2.2360679…等这些数的小数位数都是无限的,并且又不是循环的。
(2）圆周率π也是一个无限不循环小数。
无限不循环小数叫无理数.
(3）开方开不尽的数：
一般地，如果一个正数 x 的平方等于a，即 x2＝a，那么这个正数 x 就叫做 a 的算术平方根，记为“ ”，读作“根号 a ”． 特别地，我们规定0的算术平方根是0，即 ．
解: (1)因为302＝900， 所以900的算术平方根是30， 即 ; (2)因为12＝1， 所以1的算术平方根是1，即 ;
解：(3)因为 ，所以 的算术平方根是 ，即 ; (4)14的算术平方根是 .
什么叫乘方？什么叫幂？
求相同因数的积的运算叫做乘方；乘方的运算结果叫做幂。
（1）42= ，（－4）2= ；
（2） ， ；
（3）（0.8）2= ， （－0.8）2= 。
显然乘方是已知底数和指数，求幂。
如： 42已知底数4及指数2，求幂16。
反过来：如果已知一个数平方等于16，怎样求这个数？即已知指数2及幂16，求底数？？？
则 x 2 =16
∵4 2 = 16，（－4）2 = 16
∴ x = 4 或 －4
因为4 、－4的平方都等于16，我们把4及－4叫做16的平方根。
0.8、－ 0.8的平方等于0.64。那么 叫 的平方根。
什么叫数的平方根？？？
一般的，如果一个数X的平方等于a，即x2=a那么这个数X叫做a的平方根（也叫做二次方根）。
例如，因为3和-3的平方都等于9，我们就说3和-3是9的平方根。也可以说:9的平方根是±3.
如何表示一个数的平方根？
13²=169（-13）²=169，
±10叫做100的平方根
±13叫做169的平方根。
2²=4，（-2）²=4，
10²=100，（-10）²=100，
平方根的表示方法、读法
求一个数a的平方根的运算，叫做开平方.
开平方与平方是什么关系？
开平方与平方的对比填空
例2 . 求下列各数的平方根：（1）81；（2） ； （3）0.49;
解：(1)∵  (±9)2=81，
(3)∵(±0.7)2=0.49，
∴0.49的平方根为±0.7．
∴81的平方根为±9．
（1）一个正数有几个平方根？它们是什么关系？（2）0有几个平方根？（3）一个负数呢？
(1)144的平方根是什么? (2)0的平方根是什么? (3) 的平方根是什么? (4)-4的平方根是什么?为什么?从上面的回答中,你发现了什么?
一个正数a有两个平方根,它们互为相反数;0只有一个平方根，它是0本身；负数没有平方根.
（1）因为 ，所以 是 的平方根；（2） 时 ， 0 ； 0 。
（3）0的平方根可以理解成： ； 。
所以概括为 。
巩固练习:二、选择题：1、在0、－9、2、（－2）2 中，有平方根的是（ ）A、1个 B、2个 C、3个 D、4个2、数16的平方根是（ ）A、4 B、 C、 －4 D、4或－43、数0.25的平方根是（ ）A、0.5 B、0.05 C、－0.5 D、0.5或－0.54、数（－6）2的平方根是（ ）A、－6 B、6 C、6或－6 D、无平方根
判断下列说法是否正确：（1）－9的平方根是－3; ( )（2）49的平方根是7 ； ( )（3）（－2）2的平方根是±2 ；（ ）（4）－1 是 1的平方根; （ ） （5）若X2 = 16 则X = 4 （ ） （6）7的平方根是±49. ( )
平方根与算术平方根有什么异同？
平方根与算术平方根的联系与区别： 联系 （1）具有包含关系:平方根包含算术平方根，算术平方根是平方根的一种。 （2） 存在条件相同：平方根和算术平方根的被开方数都具有非负性 （3） 0的平方根和算术平方根都是0。 区别 （1） 定义不同： “如果一个数X的平方等于a，那么这个数X叫做a的平方根”， “如果一个正数x的平方等于a,即 x2 =a,那么这个正数x叫做a的算术平方根”。 （2）个数不同：一个正数有两个平方根，而一个正数的算术平方根只有一个。 （3）表示方法不同：正数a的算术平方根表示 为 ，而正数a的平方根表示为±
（1）100的平方根是 ， 的平方根是 ；（2）16的平方根是 ， 的平方根是 ；（3）0的平方根是 ； － 9 的平方根是 。
（1）为什么100、16等数有两个平方根？这两个平方根有什么关系？
（2）为什么负数的平方根是不存在？
根据以上练习回答下面两个问题：
（3）0的平方根情况又如何叙述？
例1 求下列各数的平方根:
（1） 81 （2） （3） （4）0.49 （5）169
分析 问：解题思想方法是？
答：根据平方根的定义，把求平方根转化为求平方。即求出平方等于81的所有数。
例2 下列各数有平方根吗？如果有，求出它的平方根；如果没有，请说明理由。
（1）－64 （2）0 （3）（－4）2
解：（1）因为－64是负数，所以－64没有平方根
（2）0有一个平方根，它是0；
（3）因为（－4）2=16
所以（－4）2的平方根就是16的平方根
例3 求下列各数的平方根：
(1)64 (2) (3)0.0004 (4)(-25)2 (5)11
解 (1)因为(±8)2=64，所以64平方根是±8， 即 ＝±8
（1）114的平方根是－12与12；
（2）256的平方根是16；
（3）256的平方根是－16；
（4）5是25的一个平方根；
（5）－5是25的一个平方根；
（6）1的平方根是1；
（7）－1的平方根是－1；
（8）－1是1的平方根；
（9）（－1）2的平方根－1。
如果 ，那么 就叫做 的平方根，用 来表示。当 时，有两个平方根，即 ， 表示 的正平方根， 表示负平方根。
达标训练：(1)49的平方根是（ ），算术平方根是（ ）；(2)0.09的平方根是（ ），算术平方根是（ ）； (3)若－ 是x的一个平方根，那么x的另一个平方根是（ ）；(4)平方根等于它本身的数是（ ），算术平方根等于它本身的数是（ ）；(5) 一个数的平方等于 0.01 ，这个数是（ ）；(6) √(-5)2=(7)求下列各数的平方根：0.81， ，0，√81
判断：（1）5是25的算术平方根；（2）-6是 36 的算术平方根；（3）0的算术平方根是0；（4）0.01是0.1的算术平方根；（5）-5是-25的算术平方根。
1. 求下列各数的平方根：
(1)1.44 (2)0 (3)8 (4) (5)441 (6)196 (7)10-4
2.填空：（1）25的平方根是 ；
(1)169 (2)10-6 (3) (4) (5)18
2.（1）一个正数的平方等于361，求这个正数；
（2）一个负数的平方等于121，求这个负数；
（3）一个数的平方等于196，求这个数；
3. 求满足下列各式的未知数x;
4. 求下列各式的值;
P133习题5.1 1,2题.祝你成功！
老师期望:做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去.
我们的生活离不开数学，我们要做生活的有心人。