
2020-2021学年陕西省西安市碑林区西北工大附中八年级(下)期末数学试卷
展开2020-2021学年陕西省西安市碑林区西北工大附中八年级(下)期末数学试卷
一、选择题(每小题3分,计30分)
1.(3分)用不等式表示如图所示的解集,其中正确的是( )
A.x>﹣2 B.x≥﹣2 C.x<﹣2 D.x≤﹣2
2.(3分)能判定四边形是平行四边形的是( )
A.对角线互相垂直 B.对角线相等
C.对角线互相垂直且相等 D.对角线互相平分
3.(3分)若分式有意义,则x应满足的条件为( )
A.x≠0 B.x≠1 C.x≠﹣5 D.x≠0且x≠1
4.(3分)在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C B.a:b:c=3:4:6
C.a2=c2﹣b2 D.∠A:∠B:∠C=1:2:3
5.(3分)若多项式x2+mx+n因式分解的结果为(x﹣3)•(x+1),则m,n的值分别为( )
A.﹣2,﹣3 B.﹣2,3 C.2,﹣3 D.2,3
6.(3分)在平面直角坐标系中,将线段AB平移后得到线段A'B',点A(2,1)的对应点A'的坐标为(﹣2,﹣3),则点B(﹣2,3)的对应点B'的坐标为( )
A.(6,1) B.(3,7) C.(﹣6,﹣1) D.(2,﹣1)
7.(3分)如图,在平面直角坐标系xOy中,△ABC经过中心对称变换得到△A′B′C′,那么对称中心的坐标为( )
A.(0,0) B.(﹣1,0) C.(﹣1,﹣1) D.(0,﹣1)
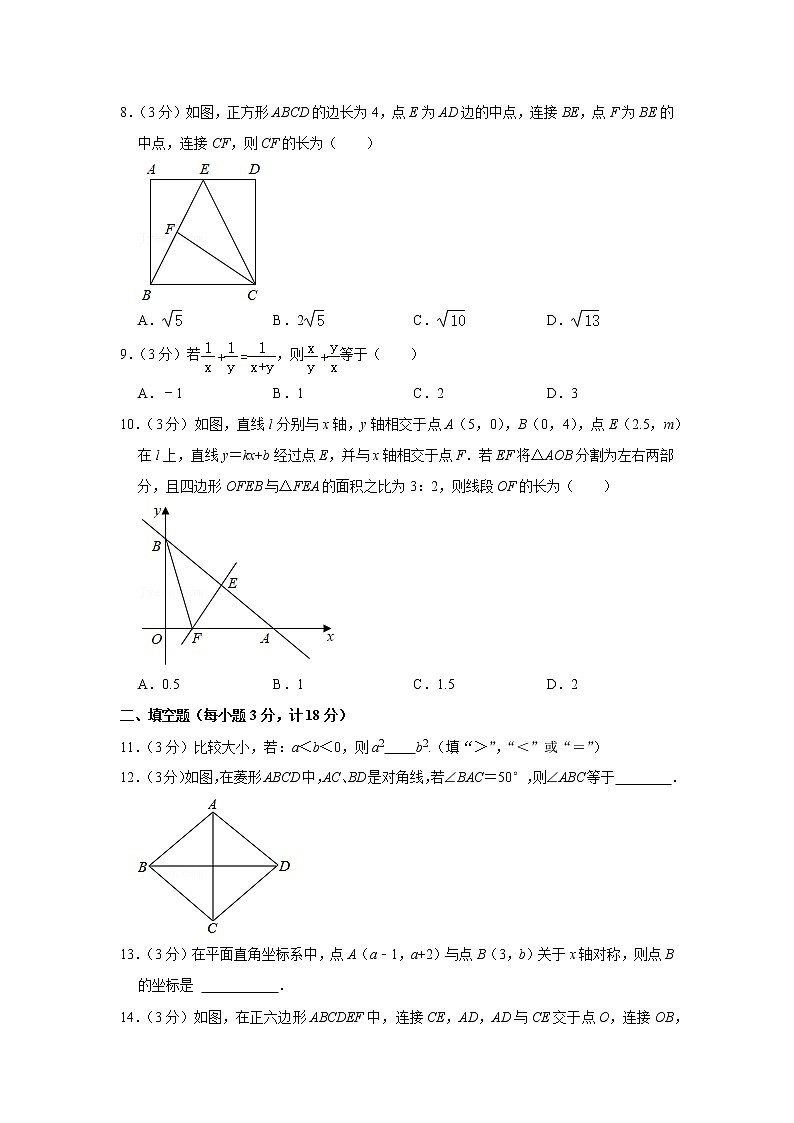
8.(3分)如图,正方形ABCD的边长为4,点E为AD边的中点,连接BE,点F为BE的中点,连接CF,则CF的长为( )
A. B.2 C. D.
9.(3分)若,则等于( )
A.﹣1 B.1 C.2 D.3
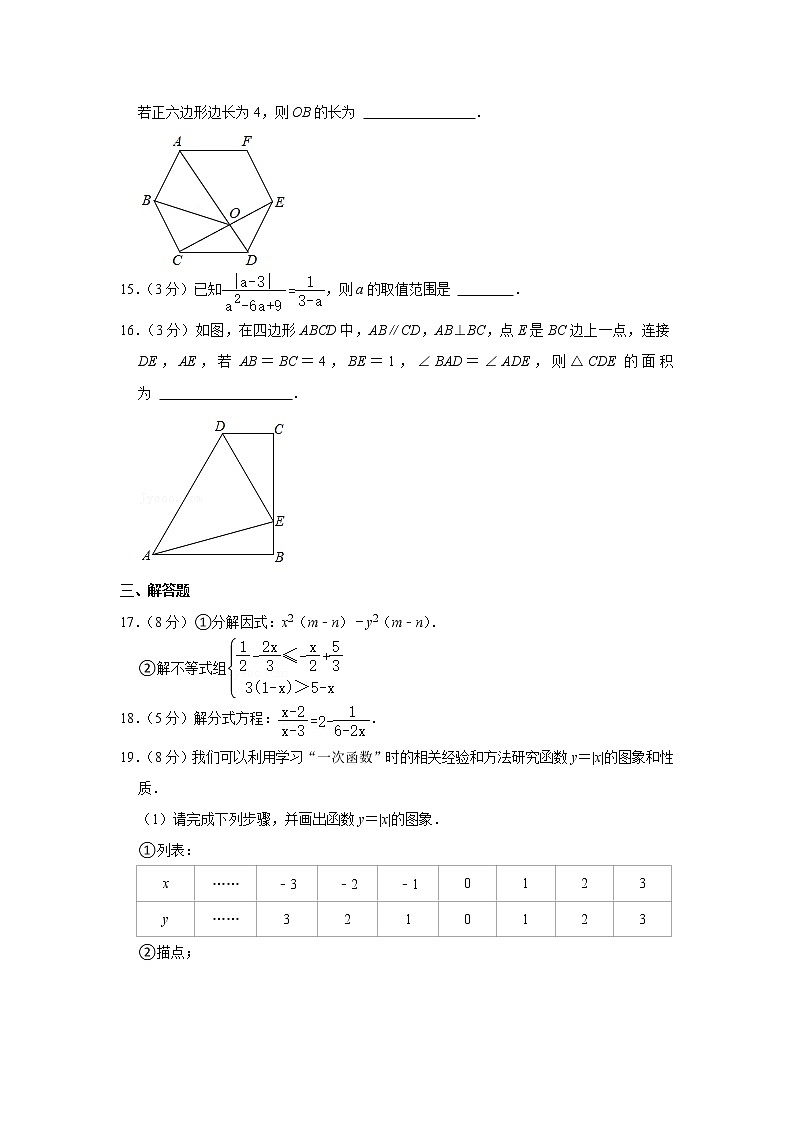
10.(3分)如图,直线l分别与x轴,y轴相交于点A(5,0),B(0,4),点E(2.5,m)在l上,直线y=kx+b经过点E,并与x轴相交于点F.若EF将△AOB分割为左右两部分,且四边形OFEB与△FEA的面积之比为3:2,则线段OF的长为( )
A.0.5 B.1 C.1.5 D.2
二、填空题(每小题3分,计18分)
11.(3分)比较大小,若:a<b<0,则a2 b2.(填“>”,“<”或“=”)
12.(3分)如图,在菱形ABCD中,AC、BD是对角线,若∠BAC=50°,则∠ABC等于 .
13.(3分)在平面直角坐标系中,点A(a﹣1,a+2)与点B(3,b)关于x轴对称,则点B的坐标是 .
14.(3分)如图,在正六边形ABCDEF中,连接CE,AD,AD与CE交于点O,连接OB,若正六边形边长为4,则OB的长为 .
15.(3分)已知,则a的取值范围是 .
16.(3分)如图,在四边形ABCD中,AB∥CD,AB⊥BC,点E是BC边上一点,连接DE,AE,若AB=BC=4,BE=1,∠BAD=∠ADE,则△CDE的面积为 .
三、解答题
17.(8分)①分解因式:x2(m﹣n)﹣y2(m﹣n).
②解不等式组
18.(5分)解分式方程:.
19.(8分)我们可以利用学习“一次函数”时的相关经验和方法研究函数y=|x|的图象和性质.
(1)请完成下列步骤,并画出函数y=|x|的图象.
①列表:
x
……
﹣3
﹣2
﹣1
0
1
2
3
y
……
3
2
1
0
1
2
3
②描点;
③连线;
(2)观察图象,当x 时,y随x的增大而增大.
(3)根据图象,不等式|x|<的解集为 .
20.(8分)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
21.(10分)如图,矩形ABCG与矩形CDEF全等点B,C,D和点C,G,F分别在同一条直线上,其中AB=CD=4,BC=DE=8.连接对角线AC,CE.
(1)在图①中,连接AE,则AE= ;
(2)如图②,将图①中的矩形CDEF绕点C逆时针旋转,当CF平分∠ACE时,求此时点E到直线AC的距离.
(3)如图③,将图①中的矩形CDEF绕点C逆时针旋转到某一个位置,连接AE,连接DG并延长交AE于点M,取AG的中点N,连接MN,求MN长的最小值.
2020-2021学年陕西省西安市碑林区西北工大附中八年级(下)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,计30分)
1.(3分)用不等式表示如图所示的解集,其中正确的是( )
A.x>﹣2 B.x≥﹣2 C.x<﹣2 D.x≤﹣2
【分析】根据解不等式,不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),可得答案.
【解答】解:在数轴上表示的解集为x<﹣2,
故选:C.
2.(3分)能判定四边形是平行四边形的是( )
A.对角线互相垂直 B.对角线相等
C.对角线互相垂直且相等 D.对角线互相平分
【分析】根据平行四边形的判定定理可知,对角线相互平分的四边形为平行四边形.
【解答】解:根据平行四边形的判定,D能判定四边形是平行四边形.
故选:D.
3.(3分)若分式有意义,则x应满足的条件为( )
A.x≠0 B.x≠1 C.x≠﹣5 D.x≠0且x≠1
【分析】利用分式分母为零,分式无意义;分母不为零,分式有意义得出答案.
【解答】解:分式有意义,
则x(x﹣1)≠0,
解得:x≠0且x≠1.
故选:D.
4.(3分)在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C B.a:b:c=3:4:6
C.a2=c2﹣b2 D.∠A:∠B:∠C=1:2:3
【分析】根据勾股定理的逆定理和三角形的内角和定理逐个判断即可.
【解答】解:A、∠A+∠B=∠C,∠C=90°,是直角三角形,不符合题意;
B、∵设a=3x,b=4x,c=6x,(3x)2+(4x)2≠(6x)2,不是直角三角形,符合题意;
C、a2=c2﹣b2,a2+b2=c2,是直角三角形,不符合题意;
D、∵∠A:∠B:∠C=1:2:3,∴∠C=90°,是直角三角形,不符合题意;
故选:B.
5.(3分)若多项式x2+mx+n因式分解的结果为(x﹣3)•(x+1),则m,n的值分别为( )
A.﹣2,﹣3 B.﹣2,3 C.2,﹣3 D.2,3
【分析】先利用乘法法则计算(x﹣3)•(x+1),再根据因式分解的意义确定m、n的值.
【解答】解:∵x2+mx+n=(x﹣3)•(x+1),
∴x2+mx+n=x2﹣2x﹣3.
∴m=﹣2,n=﹣3.
故选:A.
6.(3分)在平面直角坐标系中,将线段AB平移后得到线段A'B',点A(2,1)的对应点A'的坐标为(﹣2,﹣3),则点B(﹣2,3)的对应点B'的坐标为( )
A.(6,1) B.(3,7) C.(﹣6,﹣1) D.(2,﹣1)
【分析】根据点A到A′确定出平移规律,再根据平移规律列式计算即可得到点B′的坐标.
【解答】解:∵A(2,1)平移后得到点A′的坐标为(﹣2,﹣3),
∴向下平移了4个单位,向左平移了4个单位,
∴B(﹣2,3)的对应点B'的坐标为(﹣2﹣4,3﹣4),
即(﹣6,﹣1).
故选:C.
7.(3分)如图,在平面直角坐标系xOy中,△ABC经过中心对称变换得到△A′B′C′,那么对称中心的坐标为( )
A.(0,0) B.(﹣1,0) C.(﹣1,﹣1) D.(0,﹣1)
【分析】根据点A与点A'关于(﹣1,0)对称,点B与点B'关于(﹣1,0)对称,点C与点C′关于(﹣1,0)对称,得出△ABC与△A′B′C′关于点(﹣1,0)成中心对称.
【解答】解:由图可知,点A与点A'关于(﹣1,0)对称,点B与点B'关于(﹣1,0)对称,点C与点C′关于(﹣1,0)对称,
所以△ABC与△A′B′C′关于点(﹣1,0)成中心对称,
故选:B.
8.(3分)如图,正方形ABCD的边长为4,点E为AD边的中点,连接BE,点F为BE的中点,连接CF,则CF的长为( )
A. B.2 C. D.
【分析】过点E作EN⊥BC于N点,过F作FM⊥BC于M点,先证明△BEC为等腰三角形,再求出EN=4,FM=2,BF=,BM=1,CM=3,则在Rt△CMF中,即可求出CF=.
【解答】解:过点E作EN⊥BC于N点,过F作FM⊥BC于M点,
∵正方形的边长为4,
∴AB=CD=AD=BC=4,
∵点E为AD边的中点,
∴AE=ED=2,
∴BE=EC=2,
∴△BEC为等腰三角形,
∴BN=CN=2,
∴EN=4,
∵点F为BE的中点,
∴FM=EN=2,
∵BF=FE=,
∴BM=1,
∴CM=3,
在Rt△CMF中,CF==,
故选:D.
9.(3分)若,则等于( )
A.﹣1 B.1 C.2 D.3
【分析】根据分式的通分和完全平方公式可以将所求式子化简,然后根据,可以得到xy和(x+y)2的关系,然后代入化简后的式子即可解答本题.
【解答】解:
=
=,
∵,
∴,
∴xy=(x+y)2,
当xy=(x+y)2时,原式===﹣1,
故选:A.
10.(3分)如图,直线l分别与x轴,y轴相交于点A(5,0),B(0,4),点E(2.5,m)在l上,直线y=kx+b经过点E,并与x轴相交于点F.若EF将△AOB分割为左右两部分,且四边形OFEB与△FEA的面积之比为3:2,则线段OF的长为( )
A.0.5 B.1 C.1.5 D.2
【分析】利用待定系数法求直线AB的解析式,然后根据一次函数图象上点的坐标特点求得E点坐标,从而确定点E为AB的中点,从而结合三角形面积比计算求解.
【解答】解:设直线AB的解析式为y=kx+b,将A(5,0),B(0,4)代入,
,
解得:,
∴直线AB的解析式为:y=﹣x+4,
又∵点E(2.5,m)在AB上,
∴m=﹣×2.5+4=2,
∴E点坐标为(2.5,2),
又∵=2.5,=2,
∴点E是线段AB的中点,
∴S△FEA=S△FEB,
又∵四边形OFEB与△FEA的面积之比为3:2,
∴S△FBA与S△AOB的面积之比为4:5,
∴
∴AF=4,
∴OF=OA﹣AF=1,
故选:B.
二、填空题(每小题3分,计18分)
11.(3分)比较大小,若:a<b<0,则a2 > b2.(填“>”,“<”或“=”)
【分析】求出a+b<0,a﹣b<0,再求出a2﹣b2=(a+b)(a﹣b)>0,最后得出答案即可.
【解答】解:∵a<b<0,
∴a+b<0,a﹣b<0,
∴a2﹣b2=(a+b)(a﹣b)>0,
∴a2>b2,
故答案为:>.
12.(3分)如图,在菱形ABCD中,AC、BD是对角线,若∠BAC=50°,则∠ABC等于 80° .
【分析】根据菱形的性质得AC平分∠BAD,AD∥BC,则∠BAC=∠DAC=50°,即∠BAD=100°,然后利用两直线平行,同旁内角互补求∠ABC的度数.
【解答】解:∵四边形ABCD为菱形,
∴AC平分∠BAD,AD∥BC,
∴∠BAC=∠DAC=50°,
∴∠BAD=100°,
∵AD∥BC,
∴∠ABC+∠BAD=180°,
∴∠ABC=80°.
故答案为80°.
13.(3分)在平面直角坐标系中,点A(a﹣1,a+2)与点B(3,b)关于x轴对称,则点B的坐标是 (3,﹣6) .
【分析】直接利用关于x轴对称,横坐标相等,纵坐标互为相反数,得出a,b的值,进而得出答案.
【解答】解:∵点A(a﹣1,a+2)与点B(3,b)关于x轴对称,
∴a﹣1=3,a+2=﹣b,
解得:a=4,b=﹣6,
∴点B的坐标是(3,﹣6).
故答案为:(3,﹣6).
14.(3分)如图,在正六边形ABCDEF中,连接CE,AD,AD与CE交于点O,连接OB,若正六边形边长为4,则OB的长为 2 .
【分析】在Rt△BCO中,求出OC,可得结论.
【解答】解:在正六边形ABCDEF中,BC=CD=DE=4,∠BCD=∠CDE=120°,
∴∠DCE=∠DEC=30°,
∵AD⊥CE,
∴OC=OE=CD•cos30°=2,
∵∠BCO=∠BCD﹣∠DCO=90°,
∴OB===2,
故答案为:2.
15.(3分)已知,则a的取值范围是 a<3 .
【分析】根据绝对值的意义作答,可得答案.
【解答】解:∵==,
∴a﹣3<0.
解得a<3.
故答案是:a<3.
16.(3分)如图,在四边形ABCD中,AB∥CD,AB⊥BC,点E是BC边上一点,连接DE,AE,若AB=BC=4,BE=1,∠BAD=∠ADE,则△CDE的面积为 .
【分析】如图,过点A作AF⊥CD交CD的延长线于F,AH⊥DE于H.首先证明四边形ABCF是正方形,再证明DF=DH,EH=BE=1,设CD=x,利用勾股定理求出x,即可解决问题.
【解答】解:如图,过点A作AF⊥CD交CD的延长线于F,AH⊥DE于H.
∵AB∥CD,AB⊥BC,
∴AB⊥CD,
∴∠B=∠C=∠F=90°,
∴四边形ABCF是矩形,
∵AB=BC,
∴四边形ABCF是正方形,
∴AB=CF=BC=4,
∵CF∥AB,
∴∠ADF=∠DAB,∠DAB=∠ADE,
∴∠ADF=∠ADE,
∵AF⊥DF,AH⊥DE,
∴∠F=∠AHD=90°,
在△ADF和△ADH中,
,
∴△ADF≌△ADH(AAS),
∴DF=DH,AF=AH,
∵AF=AB,
∴AH=AB,
在Rt△AEH和Rt△AEB中,
,
∴Rt△AEH≌Rt△AEB(HL),
∴EH=BE=1,
设CD=x,则DF=DH=4﹣x,
在Rt△DCE中,x2+32=(5﹣x)2,
∴x=,
∴S△DCE=•CD•CE=××3=.
故答案为:.
三、解答题
17.(8分)①分解因式:x2(m﹣n)﹣y2(m﹣n).
②解不等式组
【分析】(1)先用提公因式法,再用公式法进行因式分解.
(2)根据不等式的基本性质解每一个不等式,再确定解集.
【解答】解:(1)x2(m﹣n)﹣y2(m﹣n)
=(m﹣n)(x2﹣y2)
=(m﹣n)(x+y)(x﹣y).
(2)将记作①式,3(1﹣x)>5﹣x记作②式.
①两边同乘6,得3﹣4x≤﹣3x+10.
移项,得﹣4x+3x≤10﹣3.
合并同类项,得﹣x≤7.
x的系数化为1,得x≥﹣7.
解②,去括号,得3﹣3x>5﹣x.
移项,得﹣3x+x>5﹣3.
合并同类项,得﹣2x>2.
x的系数化为1,得x<﹣1.
∴这个不等式组的解集是﹣7≤x<﹣1.
18.(5分)解分式方程:.
【分析】方程两边都乘以2(x﹣3)得出2(x﹣2)=4(x﹣3)+1,求出方程的解,再进行检验即可.
【解答】解:原方程化为:=2+,
方程两边都乘以2(x﹣3),得2(x﹣2)=4(x﹣3)+1,
解得:x=3.5,
检验:当x=3.5时,2(x﹣3)≠0,所以x=3.5是原方程的解,
即原方程的解是x=3.5.
19.(8分)我们可以利用学习“一次函数”时的相关经验和方法研究函数y=|x|的图象和性质.
(1)请完成下列步骤,并画出函数y=|x|的图象.
①列表:
x
……
﹣3
﹣2
﹣1
0
1
2
3
y
……
3
2
1
0
1
2
3
②描点;
③连线;
(2)观察图象,当x >0 时,y随x的增大而增大.
(3)根据图象,不等式|x|<的解集为 ﹣1<x<2 .
【分析】(1)根据画函数图象的性质可以解答本题;
(2)根据函数图象可以写出该函数图象的一条性质;
(3)根据函数图象可以得到不等式的解集.
【解答】解:(1)函数图象如图:
(2)当x>0时,y随x的增大而增大,
故答案为:>0;
(3)观察图象可得:
|x|<的解集为﹣1<x<2,
故答案为:﹣1<x<2.
20.(8分)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
【分析】(1)设去年A型车每辆售价x元,则今年售价每辆为(x﹣200)元,由卖出的数量相同建立方程求出其解即可;
(2)设今年新进A型车a辆,则B型车(60﹣a)辆,获利y元,由条件表示出y与a之间的关系式,由a的取值范围就可以求出y的最大值.
【解答】解:(1)设去年A型车每辆售价x元,则今年售价每辆为(x﹣200)元,由题意,得
=,
解得:x=2000.
经检验,x=2000是原方程的根.
答:去年A型车每辆售价为2000元;
(2)设今年新进A型车a辆,则B型车(60﹣a)辆,获利y元,由题意,得
y=(2000﹣200﹣1500)a+(2400﹣1800)(60﹣a),
y=﹣300a+36000.
∵B型车的进货数量不超过A型车数量的两倍,
∴60﹣a≤2a,
∴a≥20.
∵y=﹣300a+36000.
∴k=﹣300<0,
∴y随a的增大而减小.
∴a=20时,y有最大值,
∴B型车的数量为:60﹣20=40(辆).
∴当新进A型车20辆,B型车40辆时,这批车获利最大.
21.(10分)如图,矩形ABCG与矩形CDEF全等点B,C,D和点C,G,F分别在同一条直线上,其中AB=CD=4,BC=DE=8.连接对角线AC,CE.
(1)在图①中,连接AE,则AE= 4 ;
(2)如图②,将图①中的矩形CDEF绕点C逆时针旋转,当CF平分∠ACE时,求此时点E到直线AC的距离.
(3)如图③,将图①中的矩形CDEF绕点C逆时针旋转到某一个位置,连接AE,连接DG并延长交AE于点M,取AG的中点N,连接MN,求MN长的最小值.
【分析】(1)由矩形ABCG与矩形CDEF全等得AC=CE,再由勾股定理得=4,AE==4;
(2)由CF平分∠ACE结合等腰三角形“三线合一”得:CF⊥AE,AF=EF=4,再由等面积法得点E到直线AC的距离为;
(3)过点E作AG的平行线交DG的延长线于H,连接EG,先证明△HME≌△GMA得AM=ME,再由中位线定理得MN=,再由在矩形CDEF绕点C逆时针旋转过程中GE的范围为:CE﹣CG≤GE≤CE+CG得GE的最小值为4﹣4,故MN的最小值为2﹣2.
【解答】解:(1)∵矩形ABCG与矩形CDEF全等,
∴AC=CE,∠ACB=∠ECF,
∵∠ACB+∠ACG=90°,
∴∠ECF+∠ACG=90°,
∴∠ACE=90°,
∴AE²=AC²+CE²,
∵=4,
∴AE=4.
故答案为:4;
(2)当CF平分∠ACE时,
∵AC=CE,由等腰三角形“三线合一”得:CF⊥AE,AF=EF=4,
∴设点E到直线AC的距离为d,
则由等面积法:,
∴d=,
∴此时点E到直线AC的距离为;
(3)如图,过点E作AG的平行线交DG的延长线于H,连接EG,
∵HE∥AG,
∴∠H=∠MGA,
∵CG=CD,
∴∠CGD=∠CDG,
∵∠AGC=∠CDE=90°,
∴∠MGA+∠CGD=90°,∠CDG+∠HDE=90°,
∴∠MGA=∠HDE,
∴∠HDE=∠H,
∴HE=ED=AG,
在△HME与△GMA中,
,
∴△HME≌△GMA(AAS),
∴AM=ME,
∵AG的中点为N,
∴MN=,MN∥GE,
∵在矩形CDEF绕点C逆时针旋转过程中GE的范围为:CE﹣CG≤GE≤CE+CG,
∴4﹣4≤GE≤4+4,
∴GE的最小值为4﹣4,
∴MN的最小值为2﹣2.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/8/10 22:50:47;用户:节节高5;邮箱:5jiejg@xyh.com;学号:37675298
2021-2022学年陕西省西安市碑林区西北工大附中分校八年级(下)期末数学试卷: 这是一份2021-2022学年陕西省西安市碑林区西北工大附中分校八年级(下)期末数学试卷,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2019-2020学年陕西省西安市碑林区西北工大附中八年级(上)期中数学试卷: 这是一份2019-2020学年陕西省西安市碑林区西北工大附中八年级(上)期中数学试卷,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2019-2020学年陕西省西安市碑林区西北工大附中七年级(上)期末数学试卷: 这是一份2019-2020学年陕西省西安市碑林区西北工大附中七年级(上)期末数学试卷,共13页。试卷主要包含了选择题,填空题,解答题.等内容,欢迎下载使用。












