2017-2021年陕西中考数学真题分类汇编之统计与概率

这是一份2017-2021年陕西中考数学真题分类汇编之统计与概率，共24页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。

2017-2021年陕西中考数学真题分类汇编之统计与概率
一、选择题（共1小题）
1．（2020•陕西）如图，是市某一天的气温随时间变化的情况，则这天的日温差（最高气温与最低气温的差）是　　

A． B． C． D．
二、解答题（共10小题）
2．（2021•陕西）今年9月，第十四届全国运动会将在陕西省举行．本届全运会主场馆在西安，开幕式、闭幕式均在西安举行．某校气象兴趣小组的同学们想预估一下西安市今年9月份日平均气温状况．他们收集了西安市近五年9月份每天的日平均气温，从中随机抽取了60天的日平均气温，并绘制成如下统计图：

根据以上信息，回答下列问题：
（1）这60天的日平均气温的中位数为 　　，众数为 　　；
（2）求这60天的日平均气温的平均数；
（3）若日平均气温在的范围内（包含和为“舒适温度”．请预估西安市今年9月份日平均气温为“舒适温度”的天数．
3．（2020•陕西）小亮和小丽进行摸球试验．他们在一个不透明的空布袋内，放入两个红球，一个白球和一个黄球，共四个小球．这些小球除颜色外其它都相同．试验规则：先将布袋内的小球摇匀，再从中随机摸出一个小球，记下颜色后放回，称为摸球一次．
（1）小亮随机摸球10次，其中6次摸出的是红球，求这10次中摸出红球的频率；
（2）若小丽随机摸球两次，请利用画树状图或列表的方法，求这两次摸出的球中一个是白球、一个是黄球的概率．
4．（2020•陕西）王大伯承包了一个鱼塘，投放了2000条某种鱼苗，经过一段时间的精心喂养，存活率大致达到了．他近期想出售鱼塘里的这种鱼．为了估计鱼塘里这种鱼的总质量，王大伯随机捕捞了20条鱼，分别称得其质量后放回鱼塘．现将这20条鱼的质量作为样本，统计结果如图所示：
（1）这20条鱼质量的中位数是　　，众数是　　．
（2）求这20条鱼质量的平均数；
（3）经了解，近期市场上这种鱼的售价为每千克18元，请利用这个样本的平均数．估计王大伯近期售完鱼塘里的这种鱼可收入多少元？

5．（2019•陕西）今年植树节，某校开展了“植树造林，从我做起”的植树活动．该校参加本次植树活动的全体学生被分成了115个植树小组，按学校要求，每个植树小组至少植树10棵．经过一天的植树活动，校团委为了了解本次植树任务的完成情况，从这115个植树小组中随机抽查了10个小组，并对这10个小组植树的棵数进行了统计，结果如下：
根据以上提供的信息，解答下列问题：
（1）求所统计的这组数据的中位数和平均数；
（2）求抽查的这10个小组中，完成本次植树任务的小组所占的百分比；
（3）请你估计在本次植树活动中，该校学生共植树多少棵．

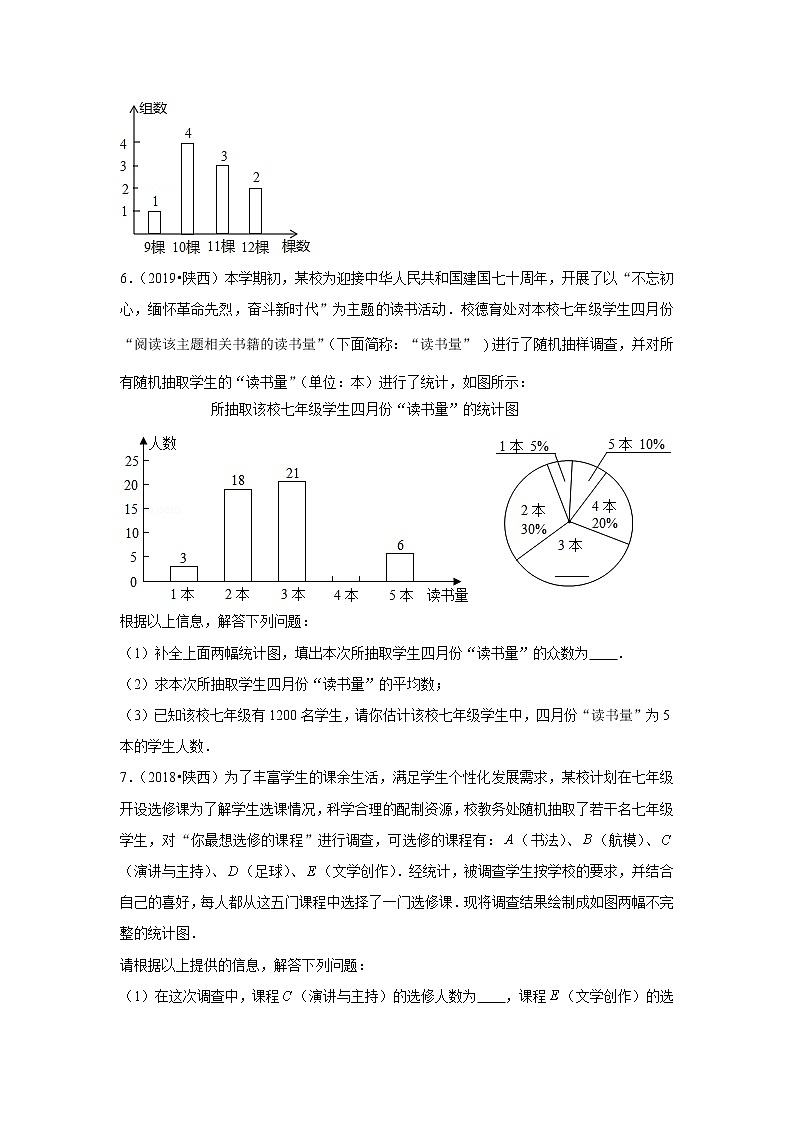
6．（2019•陕西）本学期初，某校为迎接中华人民共和国建国七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代”为主题的读书活动．校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”（下面简称：“读书量” 进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，如图所示：

根据以上信息，解答下列问题：
（1）补全上面两幅统计图，填出本次所抽取学生四月份“读书量”的众数为　　．
（2）求本次所抽取学生四月份“读书量”的平均数；
（3）已知该校七年级有1200名学生，请你估计该校七年级学生中，四月份“读书量”为5本的学生人数．
7．（2018•陕西）为了丰富学生的课余生活，满足学生个性化发展需求，某校计划在七年级开设选修课为了解学生选课情况，科学合理的配制资源，校教务处随机抽取了若干名七年级学生，对“你最想选修的课程”进行调查，可选修的课程有：（书法）、（航模）、（演讲与主持）、（足球）、（文学创作）．经统计，被调查学生按学校的要求，并结合自己的喜好，每人都从这五门课程中选择了一门选修课．现将调查结果绘制成如图两幅不完整的统计图．
请根据以上提供的信息，解答下列问题：
（1）在这次调查中，课程（演讲与主持）的选修人数为　　，课程（文学创作）的选修人数为　　；
（2）在这次调查中，哪门课程的选修人数少于各门课程选修人数的平均数？
（3）若该校七年级有900名学生，请估计该年级想选修课程（航模）的学生人数．

8．（2018•陕西）对垃圾进行分类投放，能有效提高对垃圾的处理和再利用，减少污染，保护环境．为了了解同学们对垃圾分类知识的了解程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识，某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取若干名同学进行了问卷测试．根据测试成绩分布情况，他们将全部测试成绩分成、、、四组，绘制了如下统计图表：
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别
分数分
频数
各组总分分


38
2581


72
5543


60
5100



2796
依据以上统计信息解答下列问题：
（1）求得　　，　　；
（2）这次测试成绩的中位数落在　　组；
（3）求本次全部测试成绩的平均数．

9．（2018•陕西）为了继承和发扬延安精神，满足青少年热爱红色革命根据地，了解延安革命历程的愿望，相关部门在当地中小学选拔了一批优秀共青团员和少先队员，组织他们利用节假日，在红色革命旧址（纪念馆）做“小小讲解员”，每位“小小讲解员”都要通过抽签的方式确定各自的讲解地点．讲解地点有：．枣园革命旧址，．杨家岭革命旧址，．延安革命纪念馆，．鲁艺学院旧址．抽签规则如下：
将正面分别写有字母、、、的四张卡片（除了正面字母不同外，其余均相同）背面朝上，洗匀，先由一位“小小讲解员”随机抽取一张卡片，这张卡片上的字母表示的讲解地点，即为他抽取的讲解地点，然后将卡片放回，洗匀，再由下一位“小小讲解员”抽取．已知小明和小亮都是“小小讲解员”．
（1）求小明抽到的讲解地点是“．枣园革命旧址”的概率；
（2）请用列表或画树状图的方法，求小明与小亮抽到同一讲解地点的概率．
10．（2017•陕西）养成良好的早锻炼习惯，对学生的学习和生活都非常有益，某中学为了了解七年级学生的早锻炼情况，校政教处在七年级随机抽取了部分学生，并对这些学生通常情况下一天的早锻炼时间（分钟）进行了调查．现把调查结果分成、、、四组，如表所示，同时，将调查结果绘制成下面两幅不完整的统计图．
分组
早锻炼时间分钟









请你根据以上提供的信息，解答下列问题：
（1）补全频数分布直方图和扇形统计图；
（2）所抽取的七年级学生早锻炼时间的中位数落在　 　区间内；
（3）已知该校七年级共有1200名学生，请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟．（早锻炼：指学生在早晨之间的锻炼）
11．（2017•陕西）“垃圾不落地，城市更美丽”．某中学为了了解七年级学生对这一倡议的落实情况，学校安排政教处在七年级学生中随机抽取了部分学生，并针对学生“是否随手丢垃圾”这一情况进行了问卷调查，统计结果为：为从不随手丢垃圾；为偶尔随手丢垃圾；为经常随手丢垃圾三项．要求每位被调查的学生必须从以上三项中选一项且只能选一项，现将调查结果绘制成以下两幅不完整的统计图．

请你根据以上信息，解答下列问题：
（1）补全上面的条形统计图和扇形统计图；
（2）所抽取学生“是否随手丢垃圾”情况的众数是　　；
（3）若该校七年级共有1500名学生，请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人？谈谈你的看法？

2017-2021年陕西中考数学真题分类汇编之统计与概率
参考答案与试题解析
一、选择题（共1小题）
1．（2020•陕西）如图，是市某一天的气温随时间变化的情况，则这天的日温差（最高气温与最低气温的差）是　　

A． B． C． D．
【答案】
【考点】有理数的减法；其他统计图
【专题】函数及其图象；几何直观
【分析】根据市某一天内的气温变化图，分析变化趋势和具体数值，即可求出答案．
【解答】解：从图中可以看出，这一天中最高气温是，最低气温是，
这一天中最高气温与最低气温的差为，
故选：．
【点评】本题考查了统计图，从图中得到必要的信息是解决问题的关键．
二、解答题（共10小题）
2．（2021•陕西）今年9月，第十四届全国运动会将在陕西省举行．本届全运会主场馆在西安，开幕式、闭幕式均在西安举行．某校气象兴趣小组的同学们想预估一下西安市今年9月份日平均气温状况．他们收集了西安市近五年9月份每天的日平均气温，从中随机抽取了60天的日平均气温，并绘制成如下统计图：

根据以上信息，回答下列问题：
（1）这60天的日平均气温的中位数为 　　，众数为 　　；
（2）求这60天的日平均气温的平均数；
（3）若日平均气温在的范围内（包含和为“舒适温度”．请预估西安市今年9月份日平均气温为“舒适温度”的天数．
【答案】（1），；（2）；（3）20天．
【考点】用样本估计总体；加权平均数；中位数；众数
【专题】统计的应用；数据分析观念
【分析】（1）根据中位数和众数的概念求解即可；
（2）根据加权平均数的定义列式计算即可；
（3）用样本中气温在的范围内的天数所占比例乘以今年9月份的天数即可．
【解答】解：（1）这60天的日平均气温的中位数为，众数为，
故答案为：，；
（2）这60天的日平均气温的平均数为；
（3）（天，
估计西安市今年9月份日平均气温为“舒适温度”的天数为20天．
【点评】本题主要考查众数和中位数、加权平均数、样本估计总体，一组数据中出现次数最多的数据叫做众数，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
3．（2020•陕西）小亮和小丽进行摸球试验．他们在一个不透明的空布袋内，放入两个红球，一个白球和一个黄球，共四个小球．这些小球除颜色外其它都相同．试验规则：先将布袋内的小球摇匀，再从中随机摸出一个小球，记下颜色后放回，称为摸球一次．
（1）小亮随机摸球10次，其中6次摸出的是红球，求这10次中摸出红球的频率；
（2）若小丽随机摸球两次，请利用画树状图或列表的方法，求这两次摸出的球中一个是白球、一个是黄球的概率．
【考点】列表法与树状图法
【专题】概率及其应用；推理能力
【分析】（1）由频率定义即可得出答案；
（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸出的球中一个是白球、一个是黄球的情况，利用概率公式求解即可求得答案．
【解答】解：（1）小亮随机摸球10次，其中6次摸出的是红球，这10次中摸出红球的频率；
（2）画树状图得：

共有16种等可能的结果，两次摸出的球中一个是白球、一个是黄球的有2种情况，
两次摸出的球中一个是白球、一个是黄球的概率．
【点评】本题考查的是用列表法或画树状图法求概率．注意列表法或树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率所求情况数与总情况数之比．
4．（2020•陕西）王大伯承包了一个鱼塘，投放了2000条某种鱼苗，经过一段时间的精心喂养，存活率大致达到了．他近期想出售鱼塘里的这种鱼．为了估计鱼塘里这种鱼的总质量，王大伯随机捕捞了20条鱼，分别称得其质量后放回鱼塘．现将这20条鱼的质量作为样本，统计结果如图所示：
（1）这20条鱼质量的中位数是　　，众数是　　．
（2）求这20条鱼质量的平均数；
（3）经了解，近期市场上这种鱼的售价为每千克18元，请利用这个样本的平均数．估计王大伯近期售完鱼塘里的这种鱼可收入多少元？

【考点】：用样本估计总体；：算术平均数；：中位数；：众数
【专题】542：统计的应用；65：数据分析观念
【分析】（1）根据中位数和众数的定义求解可得；
（2）利用加权平均数的定义求解可得；
（3）用单价乘以（2）中所得平均数，再乘以存活的数量，从而得出答案．
【解答】解：（1）这20条鱼质量的中位数是第10、11个数据的平均数，且第10、11个数据分别为1.4、1.5，
这20条鱼质量的中位数是，众数是，
故答案为：，．

（2），
这20条鱼质量的平均数为；

（3）（元，
答：估计王大伯近期售完鱼塘里的这种鱼可收入46980元．
【点评】本题考查了用样本估计总体、加权平均数、众数及中位数的知识，解题的关键是正确的用公式求得加权平均数，难度不大．
5．（2019•陕西）今年植树节，某校开展了“植树造林，从我做起”的植树活动．该校参加本次植树活动的全体学生被分成了115个植树小组，按学校要求，每个植树小组至少植树10棵．经过一天的植树活动，校团委为了了解本次植树任务的完成情况，从这115个植树小组中随机抽查了10个小组，并对这10个小组植树的棵数进行了统计，结果如下：
根据以上提供的信息，解答下列问题：
（1）求所统计的这组数据的中位数和平均数；
（2）求抽查的这10个小组中，完成本次植树任务的小组所占的百分比；
（3）请你估计在本次植树活动中，该校学生共植树多少棵．

【考点】：中位数；：加权平均数；：用样本估计总体
【专题】65：数据分析观念；542：统计的应用
【分析】（1）根据中位数和平均数的定义即可直接求解；
（2）利用抽查的这10个小组中完成本次植树任务的小组个数除以10即可求得完成本次植树任务的小组所占的百分比；
（3）用平均数乘植树小组的个数115即可．
【解答】解：（1）（棵；
（棵．
所统计的这组数据的中位数为10.5棵，平均数为10.6棵．
（2）．
在抽查的10个小组中，的小组完成了植树任务．
（3）（棵．
估计在本次植树活动中，该校学生共植树1219棵．
【点评】本题考查的是条形统计图的运用，读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．
6．（2019•陕西）本学期初，某校为迎接中华人民共和国建国七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代”为主题的读书活动．校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”（下面简称：“读书量” 进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，如图所示：

根据以上信息，解答下列问题：
（1）补全上面两幅统计图，填出本次所抽取学生四月份“读书量”的众数为　3　．
（2）求本次所抽取学生四月份“读书量”的平均数；
（3）已知该校七年级有1200名学生，请你估计该校七年级学生中，四月份“读书量”为5本的学生人数．
【考点】用样本估计总体；扇形统计图；条形统计图；加权平均数；众数
【专题】数据的收集与整理
【分析】（1）根据统计图可知众数为3；
（2）利用读书总量除以学生总数即得平均数；
（3）估计四月份“读书量”为5本的学生人数（人．
【解答】解：（1）根据统计图可知众数为3，

故答案为3；
（2）平均数；
（3）估计四月份“读书量”为5本的学生人数（人，
答：估计四月份“读书量”为5本的学生人数为120人．
【点评】本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
7．（2018•陕西）为了丰富学生的课余生活，满足学生个性化发展需求，某校计划在七年级开设选修课为了解学生选课情况，科学合理的配制资源，校教务处随机抽取了若干名七年级学生，对“你最想选修的课程”进行调查，可选修的课程有：（书法）、（航模）、（演讲与主持）、（足球）、（文学创作）．经统计，被调查学生按学校的要求，并结合自己的喜好，每人都从这五门课程中选择了一门选修课．现将调查结果绘制成如图两幅不完整的统计图．
请根据以上提供的信息，解答下列问题：
（1）在这次调查中，课程（演讲与主持）的选修人数为　29　，课程（文学创作）的选修人数为　　；
（2）在这次调查中，哪门课程的选修人数少于各门课程选修人数的平均数？
（3）若该校七年级有900名学生，请估计该年级想选修课程（航模）的学生人数．

【考点】：加权平均数；：用样本估计总体；：条形统计图；：扇形统计图
【专题】65：数据分析观念；54：统计与概率
【分析】（1）根据选择的人数和所占的百分比，可以求得本次调查的人数，然后可以计算出选择的人数和选择的人数；
（2）根据（1）中的结果，可以计算出各门课程选修人数的平均数，然后即可得到哪门课程的选修人数少于各门课程选修人数的平均数；
（3）根据扇形统计图中所占的百分比，可以计算出该年级想选修课程（航模）的学生人数．
【解答】解：（1）本次调查的人数为：，
选的人数为：，
选的人数为：，
故答案为：29，24；
（2），
，
足球课程的选修人数少于各门课程选修人数的平均数；
（3）（人，
答：该年级想选修课程（航模）的学生有180人．
【点评】本题考查扇形统计图、条形统计图、用样本估计总体、加权平均数，解答本题的关键是明确题意，利用数形结合的思想解答．
8．（2018•陕西）对垃圾进行分类投放，能有效提高对垃圾的处理和再利用，减少污染，保护环境．为了了解同学们对垃圾分类知识的了解程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识，某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取若干名同学进行了问卷测试．根据测试成绩分布情况，他们将全部测试成绩分成、、、四组，绘制了如下统计图表：
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别
分数分
频数
各组总分分


38
2581


72
5543


60
5100



2796
依据以上统计信息解答下列问题：
（1）求得　30　，　　；
（2）这次测试成绩的中位数落在　　组；
（3）求本次全部测试成绩的平均数．

【考点】：频数（率分布表；：扇形统计图；：加权平均数；：中位数
【专题】1：常规题型；542：统计的应用
【分析】（1）用组人数除以其所占百分比求得总人数，再用总人数减去、、组的人数可得的值，用组人数除以总人数可得的值；
（2）根据中位数的定义求解可得；
（3）根据平均数的定义计算可得．
【解答】解：（1）被调查的学生总人数为人，
，，
故答案为：30、；

（2）共有200个数据，其中第100、101个数据均落在组，
中位数落在组，
故答案为：；

（3）本次全部测试成绩的平均数为（分．
【点评】本题主要考查中位数、频数分布直方图和扇形统计图，解题的关键是根据频数分布表和扇形图得出解题所需数据，并掌握中位数的定义．
9．（2018•陕西）为了继承和发扬延安精神，满足青少年热爱红色革命根据地，了解延安革命历程的愿望，相关部门在当地中小学选拔了一批优秀共青团员和少先队员，组织他们利用节假日，在红色革命旧址（纪念馆）做“小小讲解员”，每位“小小讲解员”都要通过抽签的方式确定各自的讲解地点．讲解地点有：．枣园革命旧址，．杨家岭革命旧址，．延安革命纪念馆，．鲁艺学院旧址．抽签规则如下：
将正面分别写有字母、、、的四张卡片（除了正面字母不同外，其余均相同）背面朝上，洗匀，先由一位“小小讲解员”随机抽取一张卡片，这张卡片上的字母表示的讲解地点，即为他抽取的讲解地点，然后将卡片放回，洗匀，再由下一位“小小讲解员”抽取．已知小明和小亮都是“小小讲解员”．
（1）求小明抽到的讲解地点是“．枣园革命旧址”的概率；
（2）请用列表或画树状图的方法，求小明与小亮抽到同一讲解地点的概率．
【考点】：概率公式；：列表法与树状图法
【专题】69：应用意识；543：概率及其应用
【分析】（1）直接利用概率公式计算；
（2）画树状图展示所有16种等可能的结果数，找出小明与小亮抽到同一讲解地点的结果数，然后根据概率公式计算．
【解答】解：（1）小明抽到的讲解地点是“．枣园革命旧址”的概率；
（2）画树状图为：

共有16种等可能的结果数，其中小明与小亮抽到同一讲解地点的结果数为4，
所以小明与小亮抽到同一讲解地点的概率．
【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果，再从中选出符合事件或的结果数目，然后利用概率公式计算事件或事件的概率．
10．（2017•陕西）养成良好的早锻炼习惯，对学生的学习和生活都非常有益，某中学为了了解七年级学生的早锻炼情况，校政教处在七年级随机抽取了部分学生，并对这些学生通常情况下一天的早锻炼时间（分钟）进行了调查．现把调查结果分成、、、四组，如表所示，同时，将调查结果绘制成下面两幅不完整的统计图．
分组
早锻炼时间分钟









请你根据以上提供的信息，解答下列问题：
（1）补全频数分布直方图和扇形统计图；
（2）所抽取的七年级学生早锻炼时间的中位数落在　　区间内；
（3）已知该校七年级共有1200名学生，请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟．（早锻炼：指学生在早晨之间的锻炼）
【考点】：用样本估计总体；：频数（率分布直方图；：扇形统计图；：中位数
【分析】（1）先根据区间人数及其百分比求得总人数，再根据各区间人数之和等于总人数、百分比之和为1求得区间人数及区间百分比可得答案；
（2）根据中位数的定义求解可得；
（3）利用样本估计总体思想求解可得．
【解答】解：（1）本次调查的总人数为，
则分钟的人数为（人，
项目的百分比为，
补全图形如下：


（2）由于共有200个数据，其中位数是第100、101个数据的平均数，
则其中位数位于区间内，
故答案为：；

（3）（人，
答：估计这个年级学生中约有1020人一天早锻炼的时间不少于20分钟．
【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
11．（2017•陕西）“垃圾不落地，城市更美丽”．某中学为了了解七年级学生对这一倡议的落实情况，学校安排政教处在七年级学生中随机抽取了部分学生，并针对学生“是否随手丢垃圾”这一情况进行了问卷调查，统计结果为：为从不随手丢垃圾；为偶尔随手丢垃圾；为经常随手丢垃圾三项．要求每位被调查的学生必须从以上三项中选一项且只能选一项，现将调查结果绘制成以下两幅不完整的统计图．

请你根据以上信息，解答下列问题：
（1）补全上面的条形统计图和扇形统计图；
（2）所抽取学生“是否随手丢垃圾”情况的众数是　　；
（3）若该校七年级共有1500名学生，请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人？谈谈你的看法？
【考点】：众数；：用样本估计总体；：条形统计图；：扇形统计图
【专题】1：常规题型；542：统计的应用
【分析】（1）根据情况的人数及其所占百分比求得总人数，用总人数减去、人数求得情况的人数，再用情况人数除以总人数可得其百分比；
（2）由众数的定义解答可得；
（3）总人数乘以样本中情况的百分比可得．
【解答】解：（1）被调查的总人数为人，
情况的人数为人，情况人数所占比例为，
补全图形如下：

（2）由条形图知，情况出现次数最多，
所以众数为，
故答案为：．

（3），
答：估计该年级学生中“经常随手丢垃圾”的学生约有75人，就该年级经常随手丢垃圾的学生人数看出仍需要加强公共卫生教育、宣传和监督．
【点评】本题考查差频数分布直方图、扇形统计图、用样本估计总体，解答此类问题的关键是明确题意，找出所求问题需要的信息，利用数形结合的思想解答．

考点卡片
1．有理数的减法
（1）有理数减法法则：减去一个数，等于加上这个数的相反数． 即：a﹣b＝a+（﹣b）
（2）方法指引：
①在进行减法运算时，首先弄清减数的符号；
②将有理数转化为加法时，要同时改变两个符号：一是运算符号（减号变加号）； 二是减数的性质符号（减数变相反数）；
【注意】：在有理数减法运算时，被减数与减数的位置不能随意交换；因为减法没有交换律．
减法法则不能与加法法则类比，0加任何数都不变，0减任何数应依法则进行计算．
2．用样本估计总体
用样本估计总体是统计的基本思想．
1、用样本的频率分布估计总体分布：
从一个总体得到一个包含大量数据的样本，我们很难从一个个数字中直接看出样本所包含的信息．这时，我们用频率分布直方图来表示相应样本的频率分布，从而去估计总体的分布情况．
2、用样本的数字特征估计总体的数字特征（主要数据有众数、中位数、平均数、标准差与方差 ）．
一般来说，用样本去估计总体时，样本越具有代表性、容量越大，这时对总体的估计也就越精确．
3．频数（率）分布表
1、在统计数据时，经常把数据按照不同的范围分成几个组，分成的组的个数称为组数，每一组两个端点的差称为组距，称这样画出的统计图表为频数分布表．
2、列频率分布表的步骤：
　　（1）计算极差，即计算最大值与最小值的差．
　　（2）决定组距与组数（组数与样本容量有关，一般来说样本容量越大，分组就越多，样本容量不超过100时，按数据的多少，常分成5～12组）．
　　（3）将数据分组．
　　（4）列频率分布表．
4．频数（率）分布直方图
画频率分布直方图的步骤：
（1）计算极差，即计算最大值与最小值的差．（2）决定组距与组数（组数与样本容量有关，一般来说样本容量越大，分组就越多，样本容量不超过100时，按数据的多少，常分成5～12组）．（3）确定分点，将数据分组．（4）列频率分布表．（5）绘制频率分布直方图．
　　注：①频率分布表列出的是在各个不同区间内取值的频率，频率分布直方图是用小长方形面积的大小来表示在各个区间内取值的频率．直角坐标系中的纵轴表示频率与组距的比值，即小长方形面积＝组距×＝频率．②各组频率的和等于1，即所有长方形面积的和等于1．③频率分布表在数量表示上比较确切，但不够直观、形象，不利于分析数据分布的总体态势．④从频率分布直方图可以清楚地看出数据分布的总体态势，但是从直方图本身得不出原始的数据内容．
5．扇形统计图
（1）扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数．通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系．用整个圆的面积表示总数（单位1），用圆的扇形面积表示各部分占总数的百分数．
（2）扇形图的特点：从扇形图上可以清楚地看出各部分数量和总数量之间的关系．
（3）制作扇形图的步骤
①根据有关数据先算出各部分在总体中所占的百分数，再算出各部分圆心角的度数，公式是各部分扇形圆心角的度数＝部分占总体的百分比×360°．　　②按比例取适当半径画一个圆；按扇形圆心角的度数用量角器在圆内量出各个扇形的圆心角的度数；
④在各扇形内写上相应的名称及百分数，并用不同的标记把各扇形区分开来．
6．条形统计图
（1）定义：条形统计图是用线段长度表示数据，根据数量的多少画成长短不同的矩形直条，然后按顺序把这些直条排列起来．
（2）特点：从条形图可以很容易看出数据的大小，便于比较．
（3）制作条形图的一般步骤：
①根据图纸的大小，画出两条互相垂直的射线．
②在水平射线上，适当分配条形的位置，确定直条的宽度和间隔．
③在与水平射线垂直的射线上，根据数据大小的具体情况，确定单位长度表示多少．
④按照数据大小，画出长短不同的直条，并注明数量．
7．其他统计图
（1）根据调查项目和调查目的，设计出用于记录数据的统计表格或对统计表格中缺少的数据进行完善．表格要求简明，覆盖所有调查数据．
（2）象形统计图是表现统计数字大小和变动的各种图形总称．其中有条形统计图、扇形统计图、折线统计图、象形图等．在统计学中把利用统计图形表现统计资料的方法叫做统计图示法．其特点是：形象具体、简明生动、通俗易懂、一目了然．其主要用途有：表示现象间的对比关系；揭露总体结构；检查计划的执行情况；揭示现象间的依存关系，反映总体单位的分配情况；说明现象在空间上的分布情况．一般采用直角坐标系．横坐标用来表示事物的组别或自变量x，纵坐标常用来表示事物出现的次数或因变量y；或采用角度坐标（如圆形图）、地理坐标（如地形图）等．按图尺的数字性质分类，有实数图、累积数图、百分数图、对数图、坐标图、指数图等；其结构包括图名、图目（图中的标题）、图尺（坐标单位）、各种图线（基线、轮廓线、指导线等）、图注（图例说明、资料来源等）等．
8．算术平均数
（1）平均数是指在一组数据中所有数据之和再除以数据的个数．它是反映数据集中趋势的一项指标．
（2）算术平均数：对于n个数x1，x2，…，xn，则＝（x1+x2+…+xn）就叫做这n个数的算术平均数．
（3）算术平均数是加权平均数的一种特殊情况，加权平均数包含算术平均数，当加权平均数中的权相等时，就是算术平均数．
9．加权平均数
（1）加权平均数：若n个数x1，x2，x3，…，xn的权分别是w1，w2，w3，…，wn，则x1w1+x2w2+…+xnwnw1+w2+…+wn叫做这n个数的加权平均数．
（2）权的表现形式，一种是比的形式，如4：3：2，另一种是百分比的形式，如创新占50%，综合知识占30%，语言占20%，权的大小直接影响结果．
（3）数据的权能够反映数据的相对“重要程度”，要突出某个数据，只需要给它较大的“权”，权的差异对结果会产生直接的影响．
（4）对于一组不同权重的数据，加权平均数更能反映数据的真实信息．
10．中位数
（1）中位数：
将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．
如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
（2）中位数代表了这组数据值大小的“中点”，不易受极端值影响，但不能充分利用所有数据的信息．
（3）中位数仅与数据的排列位置有关，某些数据的移动对中位数没有影响，中位数可能出现在所给数据中也可能不在所给的数据中出现，当一组数据中的个别数据变动较大时，可用中位数描述其趋势．
11．众数
（1）一组数据中出现次数最多的数据叫做众数．
（2）求一组数据的众数的方法：找出频数最多的那个数据，若几个数据频数都是最多且相同，此时众数就是这多个数据．
（3）众数不易受数据中极端值的影响．众数也是数据的一种代表数，反映了一组数据的集中程度，众数可作为描述一组数据集中趋势的量．．
12．概率公式
（1）随机事件A的概率P（A）＝．
（2）P（必然事件）＝1．
（3）P（不可能事件）＝0．
13．列表法与树状图法
（1）当试验中存在两个元素且出现的所有可能的结果较多时，我们常用列表的方式，列出所有可能的结果，再求出概率．
（2）列表的目的在于不重不漏地列举出所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，求出概率．
（3）列举法（树形图法）求概率的关键在于列举出所有可能的结果，列表法是一种，但当一个事件涉及三个或更多元素时，为不重不漏地列出所有可能的结果，通常采用树形图．
（4）树形图列举法一般是选择一个元素再和其他元素分别组合，依次列出，象树的枝丫形式，最末端的枝丫个数就是总的可能的结果n．
（5）当有两个元素时，可用树形图列举，也可以列表列举．