2021年黑龙江省哈尔滨市南岗区虹桥中学中考数学毕业考试试卷

这是一份2021年黑龙江省哈尔滨市南岗区虹桥中学中考数学毕业考试试卷，共26页。试卷主要包含了选择题，三象限D．第二，解答题等内容，欢迎下载使用。
2021年黑龙江省哈尔滨市南岗区虹桥中学中考数学毕业考试试卷
一、选择题（每小题3分．共30分）
1．（3分）﹣9的相反数是（　　）
A．﹣9 B．﹣ C．9 D．
2．（3分）下列运算正确的是（　　）
A．＝3 B．（ab3）2＝a2b6
C．（a﹣b）2＝a2﹣b2 D．5a﹣3a＝2
3．（3分）如图所示图形中既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
4．（3分）如图中几何体的主视图是（　　）

A． B． C． D．
5．（3分）若反比例函数y＝的图象经过点（2，﹣1），则该反比例函数的图象在（　　）
A．第一、二象限 B．第一、三象限
C．第二、三象限 D．第二、四象限
6．（3分）在Rt△ABC中，∠C＝90°，∠B＝35°，AB＝3，则BC的长为（　　）
A．3sin35° B． C．3cos35° D．3tan35°
7．（3分）方程＝的解为（　　）
A．x＝ B．x＝ C．x＝ D．x＝
8．（3分）某商品经过连续两次降价，售价由原来的每件25元降到每件16元，则平均每次降价的百分率为（　　）
A．20% B．40% C．18% D．36%
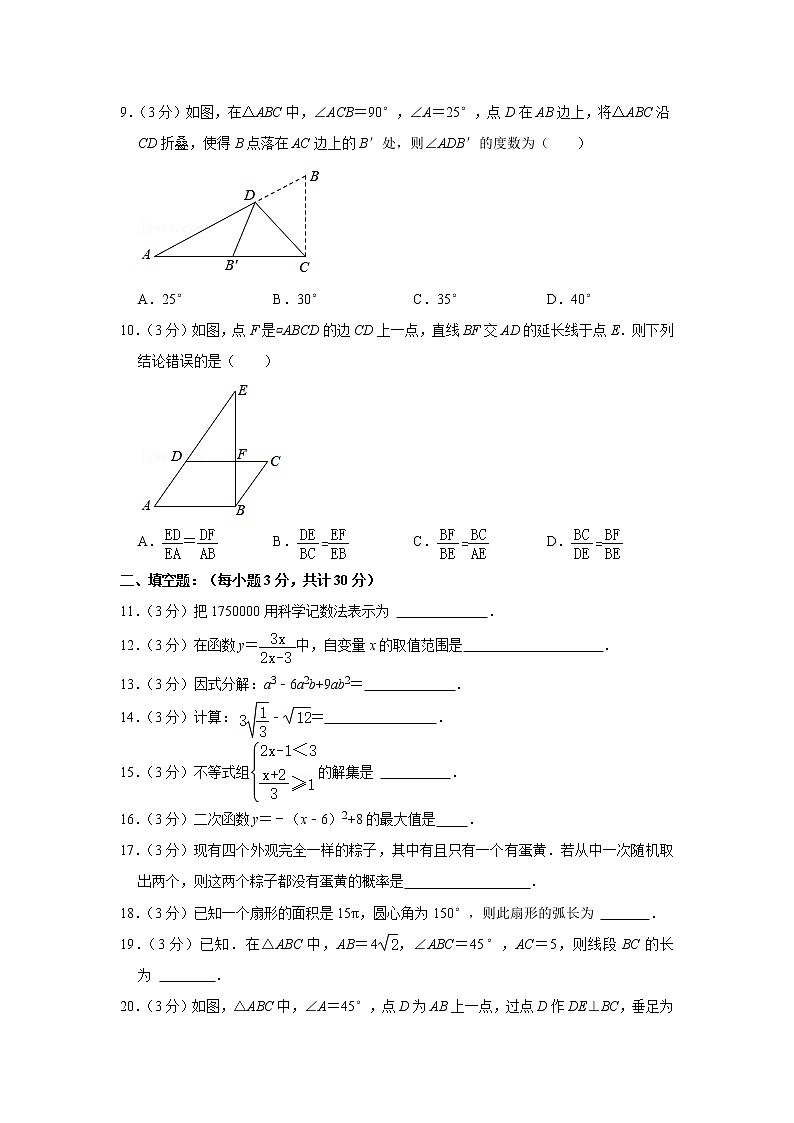
9．（3分）如图，在△ABC中，∠ACB＝90°，∠A＝25°，点D在AB边上，将△ABC沿CD折叠，使得B点落在AC边上的B′处，则∠ADB′的度数为（　　）

A．25° B．30° C．35° D．40°
10．（3分）如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线于点E．则下列结论错误的是（　　）

A．＝ B． C． D．
二、填空题：（每小题3分，共计30分）
11．（3分）把1750000用科学记数法表示为 　 　．
12．（3分）在函数y＝中，自变量x的取值范围是　 　．
13．（3分）因式分解：a3﹣6a2b+9ab2＝　 　．
14．（3分）计算：﹣＝　 　．
15．（3分）不等式组的解集是 　 　．
16．（3分）二次函数y＝﹣（x﹣6）2+8的最大值是　 　．
17．（3分）现有四个外观完全一样的粽子，其中有且只有一个有蛋黄．若从中一次随机取出两个，则这两个粽子都没有蛋黄的概率是　 　．
18．（3分）已知一个扇形的面积是15π，圆心角为150°，则此扇形的弧长为 　 　．
19．（3分）已知．在△ABC中，AB＝4，∠ABC＝45°，AC＝5，则线段BC的长为 　 　．
20．（3分）如图，△ABC中，∠A＝45°，点D为AB上一点，过点D作DE⊥BC，垂足为E，且DE＝BC，若BE＝，AC＝4，则线段AD＝　 　．

三、解答题（21、22题各7分，23、24题各8分，25-27题各10分，共计60分）
21．（7分）先化简，再求代数式（1﹣）÷的值，其中a＝4cos30°+3tan45°．
22．（7分）如图，方格纸中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．
（1）在图中画出以线段AB为一边的矩形ABCD（不是正方形），且点C和点D均在小正方形的顶点上；
（2）在图中画出以线段AB为一腰，底边长为2的等腰三角形ABE，点E在小正方形的顶点上，连接CE，请直接写出线段CE的长．

23．（8分）某学校为了解学生的课外阅读情况，王老师随机抽查部分学生，并对其暑假期间的课外阅读量进行统计分析，绘制成如图所示但不完整的统计图．已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%，根据所给出信息，解答下列问题：
（1）求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数；
（2）将条形统计图补充完整；
（3）若规定：假期阅读3本及3本以上课外书者为完成假期作业，据此估计该校1500名学生中，完成假期作业的有多少名学生？

24．（8分）如图1，AD是△ABC的中线，点E是AD中点，过A作AF∥BC交BE的延长线于F，连CF．
（1）求证：四边形ADCF是平行四边形；
（2）如图2，若AB⊥AC，请直接写出与线段AD相等的线段．

25．（10分）春平中学要为学校科技活动小组提供实验器材，计划购买A型、B型两种型号的放大镜．若购买8个A型放大镜和5个B型放大镜需用220元；若购买4个A型放大镜和6个B型放大镜需用152元．
（1）求每个A型放大镜和每个B型放大镜各多少元；
（2）春平中学决定购买A型放大镜和B型放大镜共75个，总费用不超过1180元，那么最多可以购买多少个A型放大镜？
26．（10分）已知AB、CD均为⊙O的直径，连接AC，AD，已知∠CAD＝2∠C．
（1）如图1，求证：AB⊥CD；
（2）如图2，点E在弧BC上，连接AE、DE，过点A作AE的垂线交⊙O于点F，求证：AE+AF＝DE；
（3）如图3，在（2）的条件下，连接BF交AD于点G，在AC上取点M，连接EM，若∠CME+∠CDE＝90°，EM：AF＝10：3，GF＝1，求线段DE的长度．

27．（10分）直线y＝kx+k与x轴交于A，与y轴交于C点，直线BC的解析式为y＝﹣x+k，与x轴交于B．
（1）如图1，求点A的横坐标；
（2）如图2，D为BC延长线上一点，过D作x轴垂线于点E，连接CE，若CD＝CA，设△ACE的面积为S，求S与k的函数关系式；
（3）如图3，在（2）的条件下，连接OD交AC于点F，将△CDF沿CF翻折得到△FCG，直线FG交CE于点K，若3∠ACE﹣∠CDO＝45°，求点K的坐标．


2021年黑龙江省哈尔滨市南岗区虹桥中学中考数学毕业考试试卷
参考答案与试题解析
一、选择题（每小题3分．共30分）
1．（3分）﹣9的相反数是（　　）
A．﹣9 B．﹣ C．9 D．
【分析】根据只有符号不同的两个数互为相反数，可得一个数的相反数．
【解答】解：﹣9的相反数是9，
故选：C．
2．（3分）下列运算正确的是（　　）
A．＝3 B．（ab3）2＝a2b6
C．（a﹣b）2＝a2﹣b2 D．5a﹣3a＝2
【分析】根据立方根的定义，积的乘方，完全平方公式，合并同类项判断即可．
【解答】解：A选项，33＝27，故该选项计算错误，不合题意；
B选项，（ab3）2＝a2b6，故该选项计算正确，符合题意；
C选项，（a﹣b）2＝a2﹣2ab+b2，故该选项计算错误，不合题意；
D选项，5a﹣3a＝2a，故该选项计算错误，不合题意；
故选：B．
3．（3分）如图所示图形中既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．
【解答】解：A．不是轴对称图形，也不是中心对称图形，故此选项不合题意；
B．不是轴对称图形，是中心对称图形，故此选项不合题意；
C．既是轴对称图形又是中心对称图形，故此选项符合题意；
D．是轴对称图形，但不是中心对称图形，故此选项不合题意．
故选：C．
4．（3分）如图中几何体的主视图是（　　）

A． B． C． D．
【分析】画出该组合体的主视图即可．
【解答】解：这个组合体的主视图如图所示：

故选：C．
5．（3分）若反比例函数y＝的图象经过点（2，﹣1），则该反比例函数的图象在（　　）
A．第一、二象限 B．第一、三象限
C．第二、三象限 D．第二、四象限
【分析】根据反比例函数图象在第一、三象限或在第二、四象限，根据（2，﹣1）所在象限即可作出判断．
【解答】解：点（2，﹣1）在第四象限，则该反比例函数的图象的两个分支在第二、四象限．
故选：D．
6．（3分）在Rt△ABC中，∠C＝90°，∠B＝35°，AB＝3，则BC的长为（　　）
A．3sin35° B． C．3cos35° D．3tan35°
【分析】根据余弦定义可得cosB＝，再代入AB＝3，可得答案．
【解答】解：∵cos35°＝＝，
∴BC＝3cos35°，
故选：C．

7．（3分）方程＝的解为（　　）
A．x＝ B．x＝ C．x＝ D．x＝
【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
【解答】解：去分母得：2x＝9x﹣3，
解得：x＝，
经检验x＝是分式方程的解，
故选：C．
8．（3分）某商品经过连续两次降价，售价由原来的每件25元降到每件16元，则平均每次降价的百分率为（　　）
A．20% B．40% C．18% D．36%
【分析】设降价的百分率为x，根据降低率的公式a（1﹣x）2＝b建立方程，求解即可．
【解答】解：设降价的百分率为x
根据题意可列方程为25（1﹣x）2＝16
解方程得，（舍）
∴每次降价的百分率为20%
故选：A．
9．（3分）如图，在△ABC中，∠ACB＝90°，∠A＝25°，点D在AB边上，将△ABC沿CD折叠，使得B点落在AC边上的B′处，则∠ADB′的度数为（　　）

A．25° B．30° C．35° D．40°
【分析】先根据三角形的内角和求出∠B的度数，再根据三角形翻折的性质得到∠DB′C的度数，最后根据三角形外角的性质求出∠ADB′的度数．
【解答】解：∵在△ABC中，∠ACB＝90°，∠A＝25°，
∴∠B＝180°﹣90°﹣25°＝65°，
∵△CDB′是由△CDB翻折而来，
∴∠DB′C＝∠B＝65°，
∵∠DB′C是△AB′D的外角，
∴∠ADB′＝∠DB′C﹣∠A＝65°﹣25°＝40°．
故选：D．
10．（3分）如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线于点E．则下列结论错误的是（　　）

A．＝ B． C． D．
【分析】根据矩形的性质以及平行线分线段成比例定理即可解决问题．
【解答】解：∵四边形ABCD是平行四边形，
∴BC∥DE，AD＝BC，
∴△BCF∽△EDF，
∴，
故B正确；
∵△BCF∽△EDF，
∴，
故D错误；
∵DF∥AB，
∴△EDF∽△EAB，
∴＝，故C正确，
∵△EDF∽△EAB，
∴，故A正确，
故选：D．

二、填空题：（每小题3分，共计30分）
11．（3分）把1750000用科学记数法表示为 　1.75×106　．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
【解答】解：1750000＝1.75×106．
故答案为：1.75×106．
12．（3分）在函数y＝中，自变量x的取值范围是　x≠　．
【分析】函数中分母不为零是函数y＝有意义的条件，因此2x﹣3≠0即可；
【解答】解：函数y＝中分母2x﹣3≠0，
∴x≠；
故答案为x≠；
13．（3分）因式分解：a3﹣6a2b+9ab2＝　a（a﹣3b）2　．
【分析】原式提取a，再利用完全平方公式分解即可．
【解答】解：原式＝a（a2﹣6ab+9b2）
＝a（a﹣3b）2．
故答案为：a（a﹣3b）2．
14．（3分）计算：﹣＝　　．
【分析】二次根式的加减运算，先化为最简二次根式，再将被开方数相同的二次根式进行合并．
【解答】解：原式＝﹣2＝﹣．
故答案为：﹣．
15．（3分）不等式组的解集是 　1≤x＜2　．
【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
【解答】解：解不等式2x﹣1＜3，得：x＜2，
解不等式≥1，得：x≥1，
∴不等式组的解集为1≤x＜2，
故答案为：1≤x＜2．
16．（3分）二次函数y＝﹣（x﹣6）2+8的最大值是　8　．
【分析】利用二次函数的性质解决问题．
【解答】解：∵a＝﹣1＜0，
∴y有最大值，
当x＝6时，y有最大值8．
故答案为8．
17．（3分）现有四个外观完全一样的粽子，其中有且只有一个有蛋黄．若从中一次随机取出两个，则这两个粽子都没有蛋黄的概率是　　．
【分析】根据概率的求法，先画出树状图，求出所有出现的情况，即可求出答案．
【解答】解：用A表示没蛋黄，B表示有蛋黄的，画树状图如下：

∵一共有12种情况，两个粽子都没有蛋黄的有6种情况，
∴则这两个粽子都没有蛋黄的概率是＝，
故答案为：．
18．（3分）已知一个扇形的面积是15π，圆心角为150°，则此扇形的弧长为 　5π　．
【分析】根据扇形的面积公式，可以求得该扇形所在圆的半径，然后再根据弧长公式，即可计算出该扇形的弧长．
【解答】解：∵一个扇形的面积是15π，圆心角为150°，S扇形＝，
∴15π＝，
解得r＝6，
∴此扇形的弧长为：＝5π，
故答案为：5π．
19．（3分）已知．在△ABC中，AB＝4，∠ABC＝45°，AC＝5，则线段BC的长为 　7或1　．
【分析】作AD⊥BC于点D，分类讨论点C在BD延长线上或BD上，通过解直角三角形求解．
【解答】解：作AD⊥BC于点D，

①当点C在BD延长线上时，
∵∠ABC＝45°，∠ADB＝90°，
∴△ABD为等腰直角三角形，
∴AD＝BD＝AB＝×4＝4．
在Rt△ACD中，由勾股定理得：
CD＝＝3,
∴BC＝BD+CD＝7．
②当点C'在BD上时，同理可得C'D＝AD＝4，
∴BC'＝BD﹣C'D＝1．
故答案为：7或1．
20．（3分）如图，△ABC中，∠A＝45°，点D为AB上一点，过点D作DE⊥BC，垂足为E，且DE＝BC，若BE＝，AC＝4，则线段AD＝　1　．

【分析】作CH⊥AB，由∠A＝45°，得CH＝AH＝4，设DE＝BC＝x，证明△BED∽△BHC可得BH＝，在Rt△CHB中，由勾股定理得：，解得x＝2，从而DE＝BC＝2，BH＝2，即可解决问题．
【解答】解：作CH⊥AB于H，

在Rt△ACH中，∠A＝45°，
∴CH＝AH＝sin45°×AC＝，
∵DE⊥BC，CH⊥AB，
∴∠DEB＝∠CHB＝90°，
∵∠B＝∠B，
∴△BED∽△BHC，
∴，
∴，
设DE＝BC＝x，
则BH＝，
在Rt△CHB中，由勾股定理得：
CH2+BH2＝BC2，
∴，
整理得：x4﹣16x2﹣80＝0，
∴（x2﹣20）（x2+4）＝0，
∵x2+4＞0，
∴x2＝20，
∵x＞0，
∴x＝2，
∴DE＝BC＝2，BH＝2，
在Rt△BED中，由勾股定理得：
BD＝，
∴DH＝BD﹣BH＝5﹣2＝3，
∴AD＝AH﹣DH＝4﹣3＝1．
故答案为：1．
三、解答题（21、22题各7分，23、24题各8分，25-27题各10分，共计60分）
21．（7分）先化简，再求代数式（1﹣）÷的值，其中a＝4cos30°+3tan45°．
【分析】根据分式的运算法则即可求出答案，
【解答】解：当a＝4cos30°+3tan45°时，
所以a＝2+3
原式＝•
＝
＝
22．（7分）如图，方格纸中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．
（1）在图中画出以线段AB为一边的矩形ABCD（不是正方形），且点C和点D均在小正方形的顶点上；
（2）在图中画出以线段AB为一腰，底边长为2的等腰三角形ABE，点E在小正方形的顶点上，连接CE，请直接写出线段CE的长．

【分析】（1）利用数形结合的思想解决问题即可；
（2）利用数形结合的思想解决问题即可；
【解答】解：（1）如图所示，矩形ABCD即为所求；


（2）如图△ABE即为所求，CE＝4．
23．（8分）某学校为了解学生的课外阅读情况，王老师随机抽查部分学生，并对其暑假期间的课外阅读量进行统计分析，绘制成如图所示但不完整的统计图．已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%，根据所给出信息，解答下列问题：
（1）求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数；
（2）将条形统计图补充完整；
（3）若规定：假期阅读3本及3本以上课外书者为完成假期作业，据此估计该校1500名学生中，完成假期作业的有多少名学生？

【分析】（1）根据阅读2本的学生有10人，占20%即可求得总人数；
（2）利用总人数50减去其它各组的人数就是读4本的学生数，据此即可作出统计图；
（3）求得样本中3本及3本以上课外书者所占的比例，然后乘以总人数1500即可求解．
【解答】解：（1）被抽查学生人数为：10÷20%＝50（人），中位数是3本；
（2）阅读量为4本的人数为：50﹣4﹣10﹣15﹣6＝15（人），补全条形统计图如图：

（3）×1500＝1080（本），
答：估计该校1500名学生中，完成假期作业的有1080名学生．
24．（8分）如图1，AD是△ABC的中线，点E是AD中点，过A作AF∥BC交BE的延长线于F，连CF．
（1）求证：四边形ADCF是平行四边形；
（2）如图2，若AB⊥AC，请直接写出与线段AD相等的线段．

【分析】（1）首先利用全等三角形的判定方法得出△AEF≌△DEB（AAS），进而得出AF＝BD，再利用一组对边平行且相等的四边形是平行四边形进而得出答案；
（2）由AB⊥AC，AD是BC边上的中线，可得AD＝CD＝BC，然后由四边形ADCF是平行四边形，证得四边形ADCF是菱形，即可得到和AD相等的线段．
【解答】（1）证明：∵点E是AD中点，
∴AE＝DE，
∵AF∥BC，
∴∠AFE＝∠EBD．
在△AEF和△DEB中,
,
∴△AEF≌△DEB（AAS）．
∴AF＝BD．
∵AD是△ABC的中线，
∴BD＝DC，
∴AF＝DC．
又∵AF∥BC，
∴四边形ADCF为平行四边形；
（2）解:和AD相等的线段有BD、CD、AF、CF，
理由如下：
∵AC⊥AB，AD是斜边BC的中线，
∴AD＝BC＝DC，
∵四边形ADCF是平行四边形，
∴平行四边形ADCF是菱形，
∴AD＝BD＝AF＝CF＝CD．
25．（10分）春平中学要为学校科技活动小组提供实验器材，计划购买A型、B型两种型号的放大镜．若购买8个A型放大镜和5个B型放大镜需用220元；若购买4个A型放大镜和6个B型放大镜需用152元．
（1）求每个A型放大镜和每个B型放大镜各多少元；
（2）春平中学决定购买A型放大镜和B型放大镜共75个，总费用不超过1180元，那么最多可以购买多少个A型放大镜？
【分析】（1）设每个A型放大镜和每个B型放大镜分别为x元，y元，列出方程组即可解决问题；
（2）由题意列出不等式求出即可解决问题．
【解答】解：（1）设每个A型放大镜和每个B型放大镜分别为x元，y元，可得：，
解得：，
答：每个A型放大镜和每个B型放大镜分别为20元，12元；
（2）设购买A型放大镜a个，根据题意可得：20a+12×（75﹣a）≤1180，
解得：a≤35，
答：最多可以购买35个A型放大镜．
26．（10分）已知AB、CD均为⊙O的直径，连接AC，AD，已知∠CAD＝2∠C．
（1）如图1，求证：AB⊥CD；
（2）如图2，点E在弧BC上，连接AE、DE，过点A作AE的垂线交⊙O于点F，求证：AE+AF＝DE；
（3）如图3，在（2）的条件下，连接BF交AD于点G，在AC上取点M，连接EM，若∠CME+∠CDE＝90°，EM：AF＝10：3，GF＝1，求线段DE的长度．

【分析】（1）由∠CAD＝90°，∠CAD＝2∠C，可得∠CAO＝∠C＝45°，从而∠COA＝90°，即得AB⊥CD；
（2）过点A作AH⊥DE于点H，过点B作BG⊥DE于点G，连接BE，BF，BD，由四边形AFBE是矩形，可得BE＝AF，根据∠AED＝∠ACD＝45°，得∠BEG＝45°，故AE＝AH＝HE，BE＝GE，证明△AHD≌△DGB，可得AH＝DG，即得AE+AF＝AE+BE＝AH+GE＝DG+GE＝DE；
（3）设CD与ME交于N，过D作DH⊥AE于H，连接CE、BE，设AF＝x，AE＝y，则DE＝x+y，由△DEH是等腰直角三角形，可得HE＝HD＝（x+y），AH＝（y﹣x），AD＝，Rt△AOD中，可得OA＝OD＝，即⊙O半径为，即可求CE＝y﹣x，根据∠FAG＝∠CDE，可列方程＝①，证明△CEN∽△MEC，可得＝＝，即CE2＝EM•EN，而EM＝，故EN＝，即得＝，另一方面，由△MCN∽△AED，有＝，可得＝，解得x＝y，把x＝y代入①即得y＝，从而求得DE＝x+y＝．
【解答】解：（1）∵CD为⊙O的直径，
∴∠CAD＝90°，
∵∠CAD＝2∠C，
∴∠C＝45°，
∵OA＝OC，
∴∠CAO＝∠C＝45°，
∴∠CAO+∠C＝45°+45°＝90°，
∴∠COA＝90°，
∴AB⊥CD；
（2）证明：过点A作AH⊥DE于点H，过点B作BG⊥DE于点G，连接BE，BF，BD，如图：

∵AB为⊙O的直径，AF⊥AE，
∴∠FAE＝∠AFB＝∠AEB＝90°，
∴四边形AFBE是矩形，
∴BE＝AF，
∵∠AED＝∠ACD＝45°，
由（1）知：直径AB⊥CD，
∴＝，AD＝BD，
∴∠BEG＝∠AED＝45°，
∵AH⊥DE，BG⊥DE，
∴△AHE和△BGE均为等腰直角三角形，
∴AE＝AH＝HE，BE＝GE，
∵AB为直径，
∴∠ADB＝90°，
又∵AH⊥DE，
∴∠ADE+∠DAH＝∠ADE+∠BDE＝90°，
∴∠DAH＝∠BDE，即∠DAH＝∠BDG，
在△AHD和△DGB中，
，
∴△AHD≌△DGB（AAS），
∴AH＝DG，
∴AE+AF＝AE+BE＝AH+GE＝DG+GE＝DE；
（3）设CD与ME交于N，过D作DH⊥AE于H，连接CE、BE，如图：

由（2）知：AE+AF＝DE，四边形AFBE是矩形，
设AF＝x，AE＝y，则DE＝x+y，
∵∠AED＝∠ACD＝45°，
∴△DEH是等腰直角三角形，
∴HE＝HD＝＝（x+y），
∴AH＝AE﹣HE＝y﹣（x+y）＝（y﹣x），
Rt△ADH中，AD＝＝，
Rt△AOD中，OA＝OD，OA2+OD2＝AD2，
∴OA＝OD＝，即⊙O半径为，
∴CD＝2OD＝，
∵CD为⊙O的直径，
∴∠CED＝90°，
Rt△CED中，CE＝＝＝＝|x﹣y|，
由图可知：x≤y，
∴CE＝y﹣x，
∵＝，＝，
∴＝，
∴∠FAG＝∠CDE，
∴tan∠FAG＝tan∠CDE，即＝，
∵FG＝1，
∴＝①，
∵∠CME+∠CDE＝90°，
而∠ECD+∠CDE＝90°，
∴∠CME＝∠ECD，
又∠CEN＝∠MEC，
∴△CEN∽△MEC，
∴＝＝，即CE2＝EM•EN，
∵EM：AF＝10：3，AF＝x，
∴EM＝，
∴EN＝＝，
∴＝＝＝，
∵∠EAD＝∠ECD＝∠CME，∠MCN＝∠AED＝45°，
∴△MCN∽△AED，
∴＝，
∴＝，
∴10x2+13xy﹣3y2＝0，
解得x＝﹣y（舍去）或x＝y，
把x＝y代入①得：＝，
解得：y＝，
∴x＝，
∴DE＝x+y＝．
27．（10分）直线y＝kx+k与x轴交于A，与y轴交于C点，直线BC的解析式为y＝﹣x+k，与x轴交于B．
（1）如图1，求点A的横坐标；
（2）如图2，D为BC延长线上一点，过D作x轴垂线于点E，连接CE，若CD＝CA，设△ACE的面积为S，求S与k的函数关系式；
（3）如图3，在（2）的条件下，连接OD交AC于点F，将△CDF沿CF翻折得到△FCG，直线FG交CE于点K，若3∠ACE﹣∠CDO＝45°，求点K的坐标．

【分析】（1）令y＝0，求x；
（2）过点D作y轴的垂线，由K型全等，得E点坐标，即可求出S与k的函数关系式；
（3）由等腰直角三角形和四点共圆把已知条件转化为简单的等量关系，然后求出k的值，再求点K的坐标．
【解答】解：（1）∵直线y＝kx+k与x轴交于A，与y轴交于C点，
∵当x＝0时，y＝k；
当y＝0时，kx+k＝0，得：x＝﹣1，
∴C（0，k），A（﹣1，0），
∴点A的横坐标为﹣1．
（2）过点D作DH⊥y轴于点H，
∵DH⊥OH，CO⊥AO，
∴∠DHC＝∠COA，
∴∠HDC+∠DCH＝90°，
对直线BC：当x＝0时，y＝k，当y＝0时，x＝k2，
∴B（k2，0），
∴OB＝k2，
∴，
又∵∠AOC＝∠COB＝90°，
∴△AOC∽△COB，
∴∠OAC＝∠OCB，
∵∠OAC+∠OCA＝90°，
∴∠OCB+∠OCA＝90°，即：∠ACB＝90°，
∴AC⊥BD，∠DCA＝90°，
∴∠DCH+∠ACO＝90°，
∴∠HDC＝∠OCA，
又∵DC＝CA，
∴△DHC≌△COA（AAS），
∴DH＝OC，CH＝AO，
∵A（﹣1，0），C（0，k），
∴CH＝OA＝1，DH＝CO＝k，
∴E（﹣k，0），D（﹣k，1+k），
∴AE＝﹣1﹣（﹣k）＝﹣1+k，
∴S＝（k≠0），
（3）连接AD，过AD的中点N作NM⊥AD交DE于点M，连接AM，
∵DC⊥AC，DE⊥OA，
∴∠DEA＝∠DCA＝90°，
∴在四边形AEDC中，∠DEA+∠DCA＝180°，∠EAC+∠EDC＝180°，
∴点A、D、E、C四点共圆，AD为圆的直径，点N为圆心，
∴∠ACE＝∠ADE，
∵MN是AD的中垂线，
∴DM＝AM，
∴∠ADE＝∠DAM，
∴∠AME＝2∠ADE，
∵DC＝AC，
∴∠ADC＝45°，
∴∠CDO＝45°﹣∠ADO，
又∵3∠ACE﹣∠CDO＝45°，
∴3∠ADE﹣（45°﹣∠ADO）＝45°，
即：3∠ADE+∠ADO＝90°，
在△EDO中，∠ADE+∠ADO+∠DOE＝90°，
∴∠DOE＝2∠ADE＝∠AME，
设AM＝DM＝x，则：ME＝DE﹣DM＝1+k﹣x，
∵AE2+ME2＝AM2，
∴（﹣1+k）2+（1+k﹣x）2＝x2，
解得：x＝，
∴ME＝1+k﹣，
∵∠DOE＝∠AME，
∴tan∠DOE＝tan∠AME，
∴，即：，
解得：k＝3，
∴C（0，3），D（﹣2，4），E（﹣3，0），
∴直线OD的解析式为：y＝﹣2x，
直线AC的解析式为：y＝3x+3，
直线EC的解析式为：y＝x+3，
由，解得：，
∴点F（，），
∵点D和点G关于点C对称，
∴G（3，2），
∴直线GF的解析式为：y＝，
由，解得：，
∴点K的坐标为（）．


声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2021/8/11 12:01:05；用户：节节高5；邮箱：5jiejg@xyh.com；学号：37675298