九年级上册25.1.1 随机事件教案及反思

第二十五章 概率初步

25.1 随机事件与概率

25.1.1 随机事件

【知识与技能】

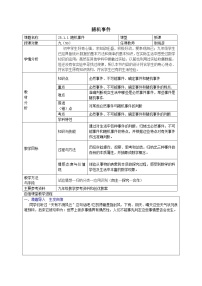
1.理解必然发生的事件,不可能发生的事件,随机事件的概念.

2.了解随机事件发生的可能性有大有小,不同的随机事件发生的可能性的大小不同.

【过程与方法】

通过本节课的学习,会根据经验判断一个简单事件是属于必然事件,不可能事件还是随机事件.

【情感态度】

感受数学与现实生活的联系,积极参与对数学问题的探讨,利用数学的思维方式解决现实问题.

【教学重点】

随机事件的特点,会判断现实生活中的随机事件.

【教学难点】

判断现实生活中哪些事件是随机事件.

一、情境导入,初步认识

1.播放一段天气预报,引出一句古语“天有不测风云”.这句话被引申为世界上有很多事情具有偶然性.人们不能事先判断这些事情是否会发生,但是随着人们对事件发生可能性的深入研究,人们发现许多偶然事件的发生也是有规律可循的.所以天气预报也只是对未来天气的预测,但并不是一定是如此.

【教学说明】激发学生的兴趣,让学生体会数学源于生活,生活中处处有数学.

2.分析说明下列事件能否一定发生.

（1）今天不上课.

（2）明天要下雨.

（3）煮熟的鸭子飞了.

（4）投一枚硬币,正面向上.

【教学说明】教师提出问题,引起学生的注意和思考.让学生感知事件的发生有多种可能.

二、思考探究,获取新知

探究1  5名同学参加演讲比赛,按抽签方式决定每个人的出场顺序,签筒中有5根形状、大小完全相同的纸签,上面分别标有出场的序号1、2、3、4、5,小军先抽签,他在看不到纸签上的数字的情况下从签筒中随机任意地取一根纸签.请考虑以下问题：

（1）抽到的序号有几种可能的结果？

（2）抽到的序号小于6吗？

（3）抽到的序号会是0吗？

（4）抽到的序号会是1吗？

【教学说明】教师提出问题,也可事先做好签,请学生们动手操作试验,感知事件发生的多种情况.经过操作试验思考回答,让学生分析阐述自己的观点,初步感知事件发生的情况类别.

（1）每次抽签的结果不一定相同,序号1、2、3、4、5都有可能抽到,共有5种可能的结果,但事先不能预料一次抽签会抽到哪种结果.

（2）抽到的序号一定小于6.

（3）抽到的序号一定不是0.

（4）抽到的序号可能是1,也可能不是1,事先无法确定.

探究2  小伟掷一个质地均匀的正方体骰子,骰子的6个面上分别刻有1到6的点数,请考虑以下问题：掷一次骰子,在骰子向上的一面上：

（1）可能出现哪些点数？

（2）出现的点数大于0吗？

（3）出现的点数会是7吗？

（4）出现的点数会是4吗？

【教学说明】教师给出问题,学生合作交流,进一步体会事件发生的情况,是一定发生,或一定不发生,还是可能发生.

1.从上述探究中可知,有些事件发生与否是可以事先确定的,有些事件发生与否,则是不能事先确定的.

【教学说明】教师引导学生归纳总结事件发生的三种情况,增强学生对事件发生可能性的认识.引导学生理解“在一定条件下”的意义.

【归纳结论】在一定条件下,有些事件必然会发生（如：标准大气压下,加热到100℃,水沸腾）,这样的事件称为必然事件.相反的,有些事件必然不会发生（如：三角形的内角和为360°）,这样的事件称为不可能事件.

在一定条件下,可能发生也可能不发生的事件（如：探究1中序号为2,探究2中出现点数为4）称为随机事件.

2.请同学们举生活中的实例说明必然事件、不可能事件、随机事件.

【教学说明】学生结合定义列举,并能稍作阐述,教师讲评、归纳、鼓励.

3.随机事件发生的可能性有大小.

探究试验：袋子中有4个黑球,2个白球,这些球的形状、大小、质地等完全相同.

在看不到球的情况下,随机的从袋子中摸出一个球.

（1）是白球还是黑球？

（2）经过多次试验,摸出的黑球和白球哪个次数多？说明了什么问题？

【教学说明】教师提出问题,引导学生试验,学生通过试验,观察结果,思考并得出结论,体会随机事件发生的可能性有大小.

【归纳结论】一般地,随机事件发生的可能性有大小,不同的随机事件发生的可能性的大小有可能不同.

三、运用新知,深化理解

1.下列事件中,属必然事件的是（  ）

A.男生的身高一定超过女生

B.方程4x2=0有实数解

C.明天数学考试小明一定得满分

D.两个无理数相加一定是无理数

2.下列事件中,哪些是随机事件？哪些是必然事件？哪些是不可能事件？说说你的理由.

(1)掷一枚骰子,6点朝上.

(2)367人中至少有2人出生日期相同.

(3)小明想用长度为10cm,20cm,30cm的小木条,首尾相接,做一个三角形.

(4)小明买福利彩票,中500万奖金.

【教学说明】上述题目较为简单,可让学生自主完成,教师再选派几名学生作出回答即可.

【答案】

1.B【解析】A.男生的身高可能超过女生,也可能不超过女生,生活中这样的现象随处可见,故它是随机事件.B.方程4x2=0的Δ=0,故它有两个相等的实数根,所以是必然事件.C.小明可能得满分,也可能不会,故为随机事件.

D.如-与相加得0是有理数,与2相加得3是无理数,故它是随机事件.

2.（1）随机事件,因为一枚骰子有6个面,其中一个面是6点.（2）必然事件,因为一年有365天或366天,所以367人必有两个生日相同.

（3）不可能事件,因为10+20=30,而三角形任意两边之和大于第三边.

（4）随机事件,因为福利彩票中包含有500万的奖项,所以只要买福利彩票是有可能中500万奖金的.

四、师生互动,课堂小结

本堂课你学到了哪些有关随机事件的知识？你有哪些收获和体会?说说看.

【教学说明】在学生回顾与反思本堂课的学习过程中,进一步完善认知,师生共同归纳总结.

1.布置作业,从教材“习题25.1”中选取.

2.完成练习册中本课时练习的“课后作业”部分.

通过这些生动的、有趣的实例,自然地引出必然事件和不可能事件；其次,必然事件和不可能事件相对于随机事件来说,特征比较明显,学生容易判断,把它们首先提出来,符合由浅入深的理念,容易激发学生的学习积极性.“抽签”这个活动是学生容易理解或亲身经历过的,操作简单省时,又具有很好的经验性,最主要的是活动中含有丰富的随机事件,激发学生的探知欲.