

2020-2021学年黑龙江省哈尔滨市道里区八年级(下)期末数学试卷(五四学制)
展开2020-2021学年黑龙江省哈尔滨市道里区八年级(下)期末数学试卷(五四学制)
一、选择题(每题3分,共30分)
1.(3分)下列选项中的方程,是一元二次方程的为( )
A.x+=1 B.x2+2y﹣3=0 C.3x2=1 D.x3﹣2x+1=0
2.(3分)线段a、b、c组成的三角形不是直角三角形的是( )
A.a=7,b=24,c=25 B.a=,b=4,c=5
C.a=,b=1,c= D.a=40,b=50,c=60
3.(3分)下列命题错误的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.一条对角线平分一组对角的四边形是菱形
D.对角线互相垂直的矩形是正方形
4.(3分)如图,在菱形ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的周长为( )
A.16 B.12 C.8 D.4
5.(3分)已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1,y2,0的大小关系是( )
A.0<y1<y2 B.y1<0<y2 C.y1<y2<0 D.y2<0<y1
6.(3分)某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( )
A.20% B.25% C.50% D.62.5%
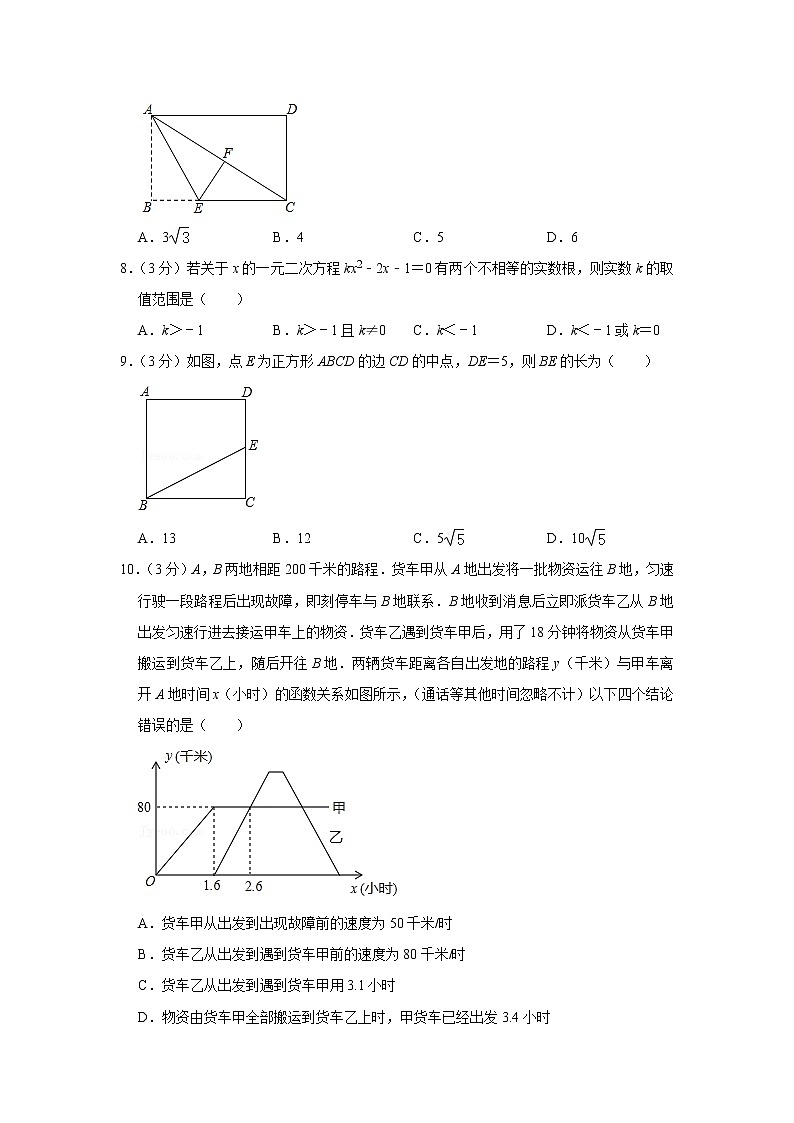
7.(3分)如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A.3 B.4 C.5 D.6
8.(3分)若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则实数k的取值范围是( )
A.k>﹣1 B.k>﹣1且k≠0 C.k<﹣1 D.k<﹣1或k=0
9.(3分)如图,点E为正方形ABCD的边CD的中点,DE=5,则BE的长为( )
A.13 B.12 C.5 D.10
10.(3分)A,B两地相距200千米的路程.货车甲从A地出发将一批物资运往B地,匀速行驶一段路程后出现故障,即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发匀速行进去接运甲车上的物资.货车乙遇到货车甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往B地.两辆货车距离各自出发地的路程y(千米)与甲车离开A地时间x(小时)的函数关系如图所示,(通话等其他时间忽略不计)以下四个结论错误的是( )
A.货车甲从出发到出现故障前的速度为50千米/时
B.货车乙从出发到遇到货车甲前的速度为80千米/时
C.货车乙从出发到遇到货车甲用3.1小时
D.物资由货车甲全部搬运到货车乙上时,甲货车已经出发3.4小时
二、填空题(每题3分,共30分)
11.(3分)函数y=中,自变量x的取值范围是 .
12.(3分)若正比例函数y=kx的图象经过点(2,﹣4),则k的值为 .
13.(3分)在△ABC中,AB=13,BC=10,BC边上的中线AD=12,则△ABC的周长为 .
14.(3分)x=2是关于x的一元二次方程ax2﹣4x﹣4=0的一个根,则a的值为 .
15.(3分)如图,在平行四边形ABCD中,∠B=60°,∠BCD的平分线交AD于点E,若CD=6,四边形ABCE的周长为26,则BC长为 .
16.(3分)一次函数y=﹣2x+3的图象不经过第 象限.
17.(3分)四边形ABCD为菱形,该菱形的周长为8,面积为2,则∠ABC为 度.
18.(3分)如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为 度.
19.(3分)参加足球联赛的每两队之间都进行两场比赛,共要比赛210场,则参加比赛的足球队共有 个.
20.(3分)如图,矩形ABCD,AB=4,AD=7,点E在BC上,CE=CD,DF⊥AE,点F为垂足,则DF的长为 .
三、解答题(第21题7分,(1)3分,(2)4分,22题7分,23,24题每题8分,第25,26,27题每题10分,共60分)
21.(7分)解下列方程:
(1)x2﹣3x=0;
(2)5x2﹣4x﹣1=0.
22.(7分)如图,每个小正方形的边长都为1,AB的位置如图所示.
(1)在图中确定点C,请你连接CA,CB,使CB⊥BA,AC=5;
(2)在完成(1)后,在图中确定点D,请你连接DA,DC,DB,使CD=,AD=,直接写出BD的长.
23.(8分)如图,在平面直角坐标系中,点O为坐标原点,直线y=2x﹣1与直线y=x+交于点A,过点A作x轴的垂线,点B为垂足,点C的横坐标为﹣1,点C在直线y=2x﹣1上,连接BC.
(1)求点A的坐标;
(2)求∠CBO的度数.
24.(8分)如图,点E,F分别在正方形ABCD的边CD,BC上,AE与DF交于点G,∠AGD=90°.
(1)求证:AE=DF;
(2)若AG=4GE,在不添加任何辅助线的情况下,请写出图中所有长度等于AB一半的线段.
25.(10分)已知某列货车挂有A,B两种不同规格的货车厢共60节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元,设使用该列车全部车厢的总费用为y万元,这列货车挂A型车厢x节.
(1)试写出y与x之间的函数关系式;
(2)若使用该列车全部车厢的总费用少于45万元,则至少挂A型车厢多少节?
26.(10分)四边形ABCD,AD∥BC,∠ABC=∠D.
(1)如图(1),求证:四边形ABCD为平行四边形;
(2)如图(2),过A,C两点分别作AE⊥BC,CF⊥AD,E,F为垂足.求证:BE=DF;
(3)如图(3),在(2)的条件下,点G在AC上,点H为四边形ABCD所在平面内一点,∠BHG=∠D=60°,∠AHG=30°,∠ACB=2∠AGH,BC=8,AG=5,求AF长.
27.(10分)在平面直角坐标系中,点O为坐标原点,过点B的直线y=﹣x+交x轴于点A,点B的横坐标为1,点C在x轴负半轴,OC=1.
(1)如图(1),求直线BC的解析式;
(2)如图(2),点P在直线BC上,点P的横坐标为t,点P在第三象限,过点P作x轴的平行线交直线AB于点Q,设PQ的长为d,求d与t之间的函数关系式,不要求写出自变量t的取值范围;
(3)如图(3),在(2)的条件下,点D在PQ上,CD⊥BC,∠BDA=45°,求d的值.
2020-2021学年黑龙江省哈尔滨市道里区八年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(每题3分,共30分)
1.(3分)下列选项中的方程,是一元二次方程的为( )
A.x+=1 B.x2+2y﹣3=0 C.3x2=1 D.x3﹣2x+1=0
【分析】根据一元二次方程的定义逐个判断即可.
【解答】解:A.是分式方程,不是整式方程,不是一元二次方程,故本选项不符合题意;
B.是二元二次方程,不是一元二次方程,故本选项不符合题意;
C.是一元二次方程,故本选项符合题意;
D.是一元三次方程,不是一元二次方程,故本选项不符合题意;
故选:C.
2.(3分)线段a、b、c组成的三角形不是直角三角形的是( )
A.a=7,b=24,c=25 B.a=,b=4,c=5
C.a=,b=1,c= D.a=40,b=50,c=60
【分析】根据判断三条线段是否能构成直角三角形的三边,需验证两小边的平方和是否等于最长边的平方,分别对每一项进行分析,即可得出答案.
【解答】解:A、72+242=252,符合勾股定理的逆定理,是直角三角形;
B、42+52=()2,符合勾股定理的逆定理,是直角三角形;
C、12+()2=()2,符合勾股定理的逆定理,是直角三角形;
D、402+502≠602,不符合勾股定理的逆定理,不是直角三角形.
故选:D.
3.(3分)下列命题错误的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.一条对角线平分一组对角的四边形是菱形
D.对角线互相垂直的矩形是正方形
【分析】利用平行四边形、矩形、菱形及正方形的判定定理分别判断后即可确定正确的选项.
【解答】解:A、对角线互相平分的四边形是平行四边形是正确的,不符合题意;
B、对角线相等的平行四边形是矩形是正确的,不符合题意;
C、一条对角线平分一组对角的四边形不一定是菱形,原来的说法错误,符合题意;
D、对角线互相垂直的矩形是正方形是正确的,不符合题意.
故选:C.
4.(3分)如图,在菱形ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的周长为( )
A.16 B.12 C.8 D.4
【分析】由菱形的性质可得出AC⊥BD,AB=BC=CD=DA,再根据直角三角形斜边上的中线等于斜边的一半得出AB的长,结合菱形的周长公式即可得出结论.
【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴△AOB为直角三角形.
∵OE=2,且点E为线段AB的中点,
∴AB=2OE=4.
C菱形ABCD=4AB=4×4=16.
故选:A.
5.(3分)已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1,y2,0的大小关系是( )
A.0<y1<y2 B.y1<0<y2 C.y1<y2<0 D.y2<0<y1
【分析】根据点的横坐标利用一次函数图象上点的坐标特征,即可求出y1、y2的值,将其与0比较大小后即可得出结论.
【解答】解:∵点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,
∴y1=﹣5,y2=10,
∵10>0>﹣5,
∴y1<0<y2.
故选:B.
6.(3分)某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( )
A.20% B.25% C.50% D.62.5%
【分析】设每月增长率为x,据题意可知:三月份销售额为2(1+x)2万元,依此等量关系列出方程,求解即可.
【解答】解:设该店销售额平均每月的增长率为x,则二月份销售额为2(1+x)万元,三月份销售额为2(1+x)2万元,
由题意可得:2(1+x)2=4.5,
解得:x1=0.5=50%,x2=﹣2.5(不合题意舍去),
答:该店销售额平均每月的增长率为50%;
故选:C.
7.(3分)如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A.3 B.4 C.5 D.6
【分析】根据折叠的性质得到AF=AB,∠AFE=∠B=90°,根据等腰三角形的性质得到AF=CF,于是得到结论.
【解答】解:∵将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,
∴AF=AB,∠AFE=∠B=90°,
∴EF⊥AC,
∵∠EAC=∠ECA,
∴AE=CE,
∴AF=CF,
∴AC=2AB=6,
故选:D.
8.(3分)若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则实数k的取值范围是( )
A.k>﹣1 B.k>﹣1且k≠0 C.k<﹣1 D.k<﹣1或k=0
【分析】利用一元二次方程的定义和判别式的意义得到k≠0且△=(﹣2)2﹣4k•(﹣1)>0,然后其出两个不等式的公共部分即可.
【解答】解:根据题意得k≠0且△=(﹣2)2﹣4k•(﹣1)>0,
解得k>﹣1且k≠0.
故选:B.
9.(3分)如图,点E为正方形ABCD的边CD的中点,DE=5,则BE的长为( )
A.13 B.12 C.5 D.10
【分析】由已知可得CD=DE=CD,CE=5,CD=10,再由勾股定理即可求BE.
【解答】解:∵点E为正方形ABCD的边CD的中点,
∴CD=DE=CD,
∵DE=5,
∴CE=5,CD=10,
在Rt△BCE中,BE==5,
故选:C.
10.(3分)A,B两地相距200千米的路程.货车甲从A地出发将一批物资运往B地,匀速行驶一段路程后出现故障,即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发匀速行进去接运甲车上的物资.货车乙遇到货车甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往B地.两辆货车距离各自出发地的路程y(千米)与甲车离开A地时间x(小时)的函数关系如图所示,(通话等其他时间忽略不计)以下四个结论错误的是( )
A.货车甲从出发到出现故障前的速度为50千米/时
B.货车乙从出发到遇到货车甲前的速度为80千米/时
C.货车乙从出发到遇到货车甲用3.1小时
D.物资由货车甲全部搬运到货车乙上时,甲货车已经出发3.4小时
【分析】根据数形结合得到甲乙相应的速度逐项判断即可.
【解答】解:由图象可得,甲货车速度为:80÷1.6=50(千米/时),故A正确;
乙货车从出发到遇到甲货车前速度为:80÷(2.6﹣1.6)=80(千米/时),故B正确;
由图可知200﹣80=120(千米),120÷80=1.5(小时),
∴货车乙从出发到遇到货车甲用1.5小时,故C错误;
物资由货车甲全部搬运到货车乙上时,甲货车已经出发:1.5+1.6+18÷60=3.4(小时),故D正确.
故选:C.
二、填空题(每题3分,共30分)
11.(3分)函数y=中,自变量x的取值范围是 x≠﹣3 .
【分析】根据分母不等于0列式计算即可得解.
【解答】解:由题意得,x+3≠0,
解得x≠﹣3.
故答案为:x≠﹣3.
12.(3分)若正比例函数y=kx的图象经过点(2,﹣4),则k的值为 ﹣2 .
【分析】因为正比例函数y=kx的图象经过点(2,﹣4),代入解析式,解之即可求得k.
【解答】解:∵正比例函数y=kx的图象经过点(2,﹣4),
∴﹣4=2k,
解得:k=﹣2.
故填﹣2.
13.(3分)在△ABC中,AB=13,BC=10,BC边上的中线AD=12,则△ABC的周长为 36 .
【分析】在△ABD中,根据勾股定理的逆定理即可判断AD⊥BC,然后根据线段的垂直平分线的性质,即可得到AC=AB,从而求解.
【解答】解:∵AD是中线,AB=13,BC=10,
∴BD=BC=5.
∵52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵BD=CD,
∴AC=AB=13,
∴△ABC的周长=13+13+10=36,
故答案为:36.
14.(3分)x=2是关于x的一元二次方程ax2﹣4x﹣4=0的一个根,则a的值为 3 .
【分析】将x=2代入原方程即可求出a的值.
【解答】解:将x=2代入ax2﹣4x﹣4=0,
∴4a﹣8﹣4=0,
∴a=3,
故答案是:3.
15.(3分)如图,在平行四边形ABCD中,∠B=60°,∠BCD的平分线交AD于点E,若CD=6,四边形ABCE的周长为26,则BC长为 5 .
【分析】利用平行四边形的对边相等且互相平行,进而得出DE=CD=6,再求出AE+BC=14,BC﹣AE=6,即可求出BC的长.
【解答】解:∵CE平分∠BCD交AD边于点E,
∴∠ECD=∠ECB,
∵在平行四边形ABCD中,AD∥BC,AB=CD=3,AD=BC,∠D=∠B=60°,
∴∠DEC=∠ECB,
∴∠DEC=∠DCE,
∴DE=CD=6,
∴△CDE是等边三角形,
∴CE=CD=6,
∵四边形ABCE的周长为26,
∴AE+BC=26﹣6﹣6=14①,
∵AD﹣AE═DE=6,
即BC﹣AE=6②,
由①②得:BC=10;
故答案为:10.
16.(3分)一次函数y=﹣2x+3的图象不经过第 三 象限.
【分析】由于k=﹣2<0,b=3>0,根据一次函数图象与系数的关系得到一次函数y=﹣2x+3的图象经过第二、四象限,与y轴的交点在x轴上方,即还要过第一象限.
【解答】解:∵k=﹣2<0,
∴一次函数y=﹣2x+3的图象经过第二、四象限,
∵b=3>0,
∴一次函数y=﹣2x+3的图象与y轴的交点在x轴上方,
∴一次函数y=﹣2x+3的图象经过第一、二、四象限,
即一次函数y=﹣2x+3的图象不经过第三象限.
故答案为三.
17.(3分)四边形ABCD为菱形,该菱形的周长为8,面积为2,则∠ABC为 30或150 度.
【分析】分当∠BAC为钝角和锐角时分别求出∠ABC的度数即可.
【解答】解:如图1所示:当∠BAC为钝角,过A作AE⊥BC,
∵菱形ABCD的周长为8,
∴AB=2,
∵面积为2,
∴AE=1,
∴∠ABC=30°,
当∠BAC为锐角是,过D作DE⊥AB,
∵菱形ABCD的周长为8,
∴AB=2,
∵面积为2,
∴AE=1,
∴∠A=30°,
∴∠ABC=150°,
故答案为:30或150.
18.(3分)如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为 60 度.
【分析】根据正方形的性质及全等三角形的性质求出∠ABE=15°,∠BAC=45°,再求∠BFC.
【解答】解:∵四边形ABCD是正方形,
∴AB=AD,
又∵△ADE是等边三角形,
∴AE=AD=DE,∠DAE=60°,
∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=(180°﹣150°)÷2=15°,
又∵∠BAC=45°,
∴∠BFC=45°+15°=60°.
故答案为:60.
19.(3分)参加足球联赛的每两队之间都进行两场比赛,共要比赛210场,则参加比赛的足球队共有 15 个.
【分析】设共有x个队参加比赛,根据每两队之间都进行两场比赛结合共比了210场即可得出关于x的一元二次方程,解之即可得出结论.
【解答】解:设共有x个队参加比赛,
根据题意得:2×x(x﹣1)=210,
整理得:x2﹣x﹣210=0,
解得:x=15或x=﹣14(舍去).
故答案为:15.
20.(3分)如图,矩形ABCD,AB=4,AD=7,点E在BC上,CE=CD,DF⊥AE,点F为垂足,则DF的长为 .
【分析】两三角形相似,只要证明∠B=∠AFD,∠AEB=∠DAE即可得出△ABE与△DFA相似,进而解答即可.
【解答】解:∵矩形ABCD,
∴AD∥BC,
∴∠DAE=∠AEB,
∵DF⊥AE,
∴∠B=∠AFD=90°,
在△ABE与△DFA中:
∠B=∠AFD,∠AEB=∠DAE
∴△ABE∽△DFA.
∴,
即=,
解得:DF=,
故答案为:.
三、解答题(第21题7分,(1)3分,(2)4分,22题7分,23,24题每题8分,第25,26,27题每题10分,共60分)
21.(7分)解下列方程:
(1)x2﹣3x=0;
(2)5x2﹣4x﹣1=0.
【分析】(1)先分解因式,即可把一元二次方程转化成一元一次方程,求出方程的解即可;
(2)先分解因式,即可把一元二次方程转化成一元一次方程,求出方程的解即可.
【解答】解:(1)x2﹣3x=0,
x(x﹣3)=0,
x=0,x﹣3=0,
x1=0,x2=3;
(2)5x2﹣4x﹣1=0,
(5x+1)(x﹣1)=0,
5x+1=0,x﹣1=0,
x1=﹣,x2=1.
22.(7分)如图,每个小正方形的边长都为1,AB的位置如图所示.
(1)在图中确定点C,请你连接CA,CB,使CB⊥BA,AC=5;
(2)在完成(1)后,在图中确定点D,请你连接DA,DC,DB,使CD=,AD=,直接写出BD的长.
【分析】(1)先证明∠ABE=∠BCF,∠DBF=∠BAE,则可得到∠CBF+∠BCF=90°,从而确定C点位置;
(2)由勾股定理在Rt△DBG中,可求BD的长.
【解答】解:(1)如图,
在Rt△AEB中,tan∠ABE=,
在Rt△BCF中,tan∠BCF=,
∴∠ABE=∠BCF,
∴∠DBF=∠BAE,
∴∠CBF+∠ABE=∠CBF+∠BCF=90°,
∴BC⊥AB,
在Rt△ACH中,AC=5;
(2)∵CD=,AD=,可确定D点位置如图,
∴在Rt△DBG中,BD=.
23.(8分)如图,在平面直角坐标系中,点O为坐标原点,直线y=2x﹣1与直线y=x+交于点A,过点A作x轴的垂线,点B为垂足,点C的横坐标为﹣1,点C在直线y=2x﹣1上,连接BC.
(1)求点A的坐标;
(2)求∠CBO的度数.
【分析】(1)解析式联立成方程组,解方程组即可求得A的坐标;
(2)过C点作CD⊥x轴于D,根据A的坐标以及直线y=2x﹣1求得B、C的坐标,即可求得BD=CD=3,从而求得∠CBO=45°.
【解答】解:(1)由,解得,
∴A(2,3);
(2)过C点作CD⊥x轴于D,
∵A(2,3),
∴B(2,0),
∵点C的横坐标为﹣1,点C在直线y=2x﹣1上,
∴y=2×(﹣1)﹣1=﹣3,
∴C(﹣1,﹣3),
∴BD=3,CD=3,
∴△CBD的等腰直角三角形,
∴∠CBO=45°.
24.(8分)如图,点E,F分别在正方形ABCD的边CD,BC上,AE与DF交于点G,∠AGD=90°.
(1)求证:AE=DF;
(2)若AG=4GE,在不添加任何辅助线的情况下,请写出图中所有长度等于AB一半的线段.
【分析】(1)证明△AED≌△DFC(AAS)即可;
(2)设GE=a,则AG=4a,可证△ADE∽△AGD,则正方形的边长为AD=2a,所以DE=FC=BF=CE=a,即可求解.
【解答】解:(1)∵正方形ABCD,
∴AD=CD,∠ADC=∠DCF=90°,
∵∠AGD=90°
∴∠FDC+∠DEA=90°,
∵∠FDC+∠DFC=90°,
∴∠DEA=∠DFC,
∴△AED≌△DFC(AAS),
∴AE=DF;
(2)∵AG=4GE,
设GE=a,则AG=4a,
∵∠DGA=∠ADE,
∴△ADE∽△AGD,
∴=,
∴AD=2a,
在Rt△ADE中,DE=a,
∵△AED≌△DFC,
∴FC=a,
∵CD=BC=2a,
∴BF=CE=a,
∴长度等于AB一半的线段有DE、CE、CF、BF.
25.(10分)已知某列货车挂有A,B两种不同规格的货车厢共60节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元,设使用该列车全部车厢的总费用为y万元,这列货车挂A型车厢x节.
(1)试写出y与x之间的函数关系式;
(2)若使用该列车全部车厢的总费用少于45万元,则至少挂A型车厢多少节?
【分析】(1)先变换单位,设用A型车厢x节,则用B型车厢(60﹣x)节,总运费为y万元,根据题意列出函数关系式;
(2)根据用该列车全部车厢的总费用少于45万元列出不等式求解即可.
【解答】解:(1)6000元=0.6万元,8000元=0.8万元,
设用A型车厢x节,则用B型车厢(60﹣x)节,总运费为y万元,
依题意,得y=0.6x+0.8(60﹣x)=﹣0.2x+48;
(2)由题意,得﹣0.2x+48<45,
解得:x>15,
∵x为正整数,
∴x的最小值为16,
答:该列车全部车厢的总费用少于45万元,则至少挂A型车厢16节.
26.(10分)四边形ABCD,AD∥BC,∠ABC=∠D.
(1)如图(1),求证:四边形ABCD为平行四边形;
(2)如图(2),过A,C两点分别作AE⊥BC,CF⊥AD,E,F为垂足.求证:BE=DF;
(3)如图(3),在(2)的条件下,点G在AC上,点H为四边形ABCD所在平面内一点,∠BHG=∠D=60°,∠AHG=30°,∠ACB=2∠AGH,BC=8,AG=5,求AF长.
【分析】(1)根据两对边分别平行证四边形为平行四边形即可;
(2)根据AAS证△ABE≌△CDF,即可得证结论;
(3)延长HG交BC延长线于点P,延长BA至点Q,使AQ=AG,连接HQ,在HG上截取HR=HB,连接RB,证△HAQ≌△HAG,△BHQ≌△BRP,得出BC+CG=BA+AG,设CG=x,则AC=5+x,AB=3+x,根据30°所对的直角边是斜边的一半再利用勾股定理求出x=2,即可求出AF.
【解答】解:(1)∵AD∥BC,
∴∠D+∠BCD=180°,
∵∠ABC=∠D,
∴∠ABC+∠BCD=180°,
∴AB∥CD,
∵AD∥BC,
∴四边形ABCD为平行四边形;
(2)由四边形ABCD为平行四边形,
得AB=CD,∠ABC=∠D,
∵AE⊥BC,CF⊥AD,
∴∠AEB=∠CFD=90°,
∴△ABE≌△CDF(AAS),
∴BE=DF;
(3)如图(3),延长HG交BC延长线于点P,延长BA至点Q,使AQ=AG,延长CA交HQ于点M,连接HQ,在HG上截取HR=HB,连接RB,
∵∠BHG=∠D=60°,∠AHG=30°,∠ACB=2∠AGH,
∴∠MAH=∠AHG+∠AGH=30°+∠AGH,∠MAB=∠ABC+∠ACB=60°+2∠AGH,
∴∠MAH=∠MAB,
即∠MAH=∠BAH,
又∵∠MAQ=∠BAC,
∴∠MAH+∠MAQ=∠BAC+∠BAH,
即∠HAQ=∠HAG,
又∵AQ=AG,AH=AH,
∴△HAQ≌△HAG(SAS),
∴∠QHA=∠AHG=30°,∠Q=∠AGH,
∴∠QHB=∠QHA+∠AHG+∠BHG=30°+30°+60°=120°,
∵HR=HB,∠BHG=60°,
∴△BHR是等边三角形,
∴BH=BR,∠HBR=60°,
∴∠HBA+∠ABR=∠ABR+∠RBC=60°,
∴∠HBA=∠RBC,
∴△HBQ≌△RBP(ASA),
∴BQ=BP,∠Q=∠P,
∵∠AGH=∠PGC,
∴∠PGC=∠AGH=∠P,
∴CG=CP,
∴BC+CP=BA+AQ,
即BC+CG=BA+AG,
设CG=x,则AC=5+x,AB=BQ﹣AQ=BC+PC﹣AG=8+x﹣5=3+x,
∵∠ABE=60°,
∴∠BAE=90°﹣∠ABE=90°﹣60°=30°,
∴BE=AB=,CE=BC﹣BE=8﹣=,
由勾股定理得AB2﹣BE2=AC2﹣EC2,
即(3+x)2﹣()2=(5+x)2﹣()2,
解得x=2,
∴AF=EC=,
即AF的长为.
27.(10分)在平面直角坐标系中,点O为坐标原点,过点B的直线y=﹣x+交x轴于点A,点B的横坐标为1,点C在x轴负半轴,OC=1.
(1)如图(1),求直线BC的解析式;
(2)如图(2),点P在直线BC上,点P的横坐标为t,点P在第三象限,过点P作x轴的平行线交直线AB于点Q,设PQ的长为d,求d与t之间的函数关系式,不要求写出自变量t的取值范围;
(3)如图(3),在(2)的条件下,点D在PQ上,CD⊥BC,∠BDA=45°,求d的值.
【分析】(1)根据过点B的直线y=﹣x+交x轴于点A,点B的横坐标为1,求得点B的坐标,根据点C在x轴负半轴,OC=1可求得点C的坐标,利用待定系数法即可求得直线BC的解析式;
(2)求出P、Q两点坐标即可解决问题;
(3)作BF⊥x轴,点F为垂足,作BG⊥BA,使BG=BA,连接CG,作GH⊥BF,点H为垂足,作GT⊥x轴,点T为垂足,过点B作BD的垂线交DA的延长线于点M,作DN⊥x轴,点N为垂足,证明△GBH≌△BAF(AAS),可得G(﹣3,1),求出BC=2,CG=,BG=5,由勾股定理的逆定理得∠BCG=90°,G,C,D 三点共线,证明△BGD≌△BAM(SAS),可得∠BDC=∠M=45°,△BCD为等腰直角三角形,再证Rt△BCF≌Rt△CDN(AAS),可得DN=CF=2,则点P的纵坐标为﹣2,求出t=﹣2,利用(2)求得的d与t之间的函数关系式即可求解.
【解答】解:(1)∵过点B的直线y=﹣x+交x轴于点A,点B的横坐标为1,
∴点B的坐标是(1,4),
又∵点C在x轴负半轴,OC=1,
∴C(﹣1,0),
设直线BC的解析式为:y=kx+b(k≠0),
则,
解得:.
∴直线BC的解析式为:y=2x+2;
(2)∵点P在直线BC上,点P的横坐标为t,
∴P(t,2t+2),
∵点Q在直线AB上,PQ∥x轴,直线AB:y=﹣x+,
∴2t+2=﹣x+,解得:x=,
∴Q(,2t+2),
∴d=PQ=﹣t=;
(3)作BF⊥x轴,点F为垂足,作BG⊥BA,使BG=BA,连接CG,作GH⊥BF,点H为垂足,作GT⊥x轴,点T为垂足,过点B作BD的垂线交DA的延长线于点M,作DN⊥x轴,点N为垂足,
∴∠BHG=∠AFB=90°,∠ABG=90°,
∴∠GBH=∠BAF,
∵BG=BA,
∴△GBH≌△BAF(AAS),
∴BH=AF,GH=BF.
∵B(1,4),A(4,0),C(﹣1,0),
∴OF=1,OA=4,BF=4,BC=2,
∴AF=3,AB=BG==5,GH=BF=4,OG=3,BH=AF=3,
∴HF=GT=1,
∴G(﹣3,1),
∴CG=,
∵BC=2,CG=,BG=5,
∴BC2+CG2=BG2,
∴∠BCG=90°,
∵CD⊥BC,
∴∠GCB+∠DCB=180°,
∴G,C,D 三点共线,
∵BG⊥BA,BD⊥BM,
∴∠GBD=∠ABM,
∵∠BDA=45°,
∴BD=BM,∠M=45°,
∵BG=BA,
∴△BGD≌△BAM(SAS),
∴∠BDC=∠M=45°,
∴△BCD为等腰直角三角形,
∴BC=CD,
∵BF⊥x轴,CD⊥BC,DN⊥x轴,
∴∠CBF=∠DCN,∠BFC=∠CND=90°
∴Rt△BCF≌Rt△CDN(AAS),
∴DN=CF,
∵BC=2,BF=4,
∴DN=CF==2,
∵PQ∥x轴,点D在PQ上,
∴点P的纵坐标为﹣2,即2t+2=﹣2,解得:t=﹣2,
由(2)得:
d==.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/8/12 11:43:18;用户:节节高5;邮箱:5jiejg@xyh.com;学号:37675298
2022-2023学年黑龙江省哈尔滨市道里区八年级(上)期末数学试卷(五四学制)(含解析): 这是一份2022-2023学年黑龙江省哈尔滨市道里区八年级(上)期末数学试卷(五四学制)(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
黑龙江省哈尔滨市道里区光华中学校2020-2021学年八年级上学期期中数学试卷(五四学制): 这是一份黑龙江省哈尔滨市道里区光华中学校2020-2021学年八年级上学期期中数学试卷(五四学制),共3页。
2022-2023学年黑龙江省哈尔滨市道里区七年级(下)期末数学试卷(五四学制)(含解析): 这是一份2022-2023学年黑龙江省哈尔滨市道里区七年级(下)期末数学试卷(五四学制)(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












