
2018年湖北省武汉市华中师大一附中高中招生数学试卷
展开
这是一份2018年湖北省武汉市华中师大一附中高中招生数学试卷,共17页。试卷主要包含了a的值为 ,2018的值为 等内容,欢迎下载使用。
2018年湖北省武汉市华中师大一附中高中招生数学试卷
一.选择题(本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,有且只有-项是正确的。)
1.(7分)二次函数y=x2+2x+c的图象与x轴的两个交点为A(x1,0),B(x2,0),且x1<x2,点P(m,n)是图象上一点,那么下列判断正确的是( )
A.当n>0时,m<x1 B.当n>0时,m>x2
C.当n<0时,m<0 D.当n<0时,x1<m<x2
2.(7分)已知实数a、b、c满足a<b<c,并且k=++,则直线y=﹣kx+k一定经过( )
A.第一、三、四象限 B.第一、二、四象限
C.第一、二、三象限 D.第二、三、四象限
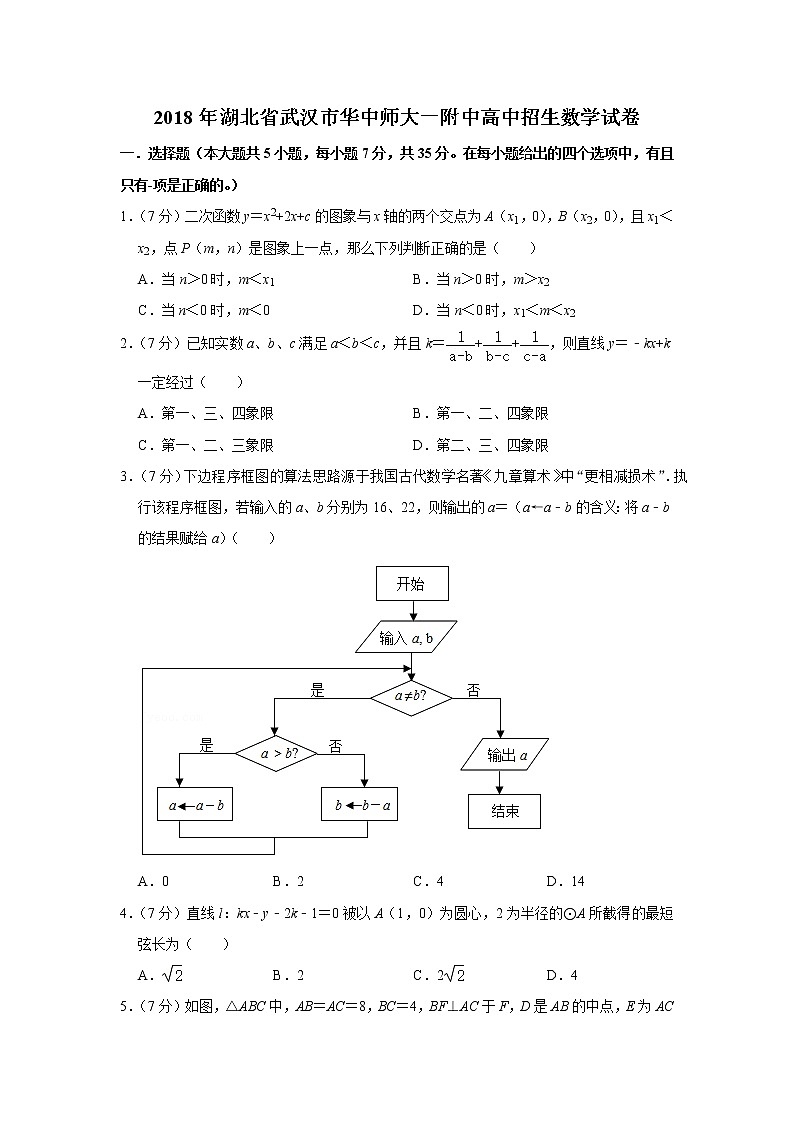
3.(7分)下边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图,若输入的a、b分别为16、22,则输出的a=(a←a﹣b的含义:将a﹣b的结果赋给a)( )
A.0 B.2 C.4 D.14
4.(7分)直线l:kx﹣y﹣2k﹣1=0被以A(1,0)为圆心,2为半径的⊙A所截得的最短弦长为( )
A. B.2 C.2 D.4
5.(7分)如图,△ABC中,AB=AC=8,BC=4,BF⊥AC于F,D是AB的中点,E为AC上一点,且2EF=AC,则tan∠DEF=( )
A. B. C. D.
二、填空题(本大题共5小题,每小题7分,共35分)
6.(7分)若a+b﹣2﹣4=3﹣c﹣5,则(b﹣c)a的值为 .
7.(7分)已知△ABC的一边长为4,另外两边长恰是方程2x2﹣12x+m+1=0的两实根,则实数m的取值范围是 .
8.(7分)点D是△ABC的边AB上的一点,使得AB=3AD,P是△ABC外接圆上一点,使得∠ADP=∠ACB,则的值为 .
9.(7分)有十张正面分别标有数字1,2,3,4,5,6,7,8,9,10的不透明卡片,它们除数字不同外其余全部相同,将它们背面朝上,洗匀后从中任取一张,以卡片上的数字作为关于x的不等式5x﹣a≤5中的系数a,使得该不等式的正整数解只有1和2的概率为 .
10.(7分)若四个互不相等的正实数a,b,c,d满足(a2018﹣c2018)(a2018﹣d2018)=2018,(b2018﹣c2018)(b2018﹣d2018)=2018,则(ab)2018﹣(cd)2018的值为 .
三、解答题(本大题共3小题,共50分解答应写出文字说明、证明过程和演算步骤.)
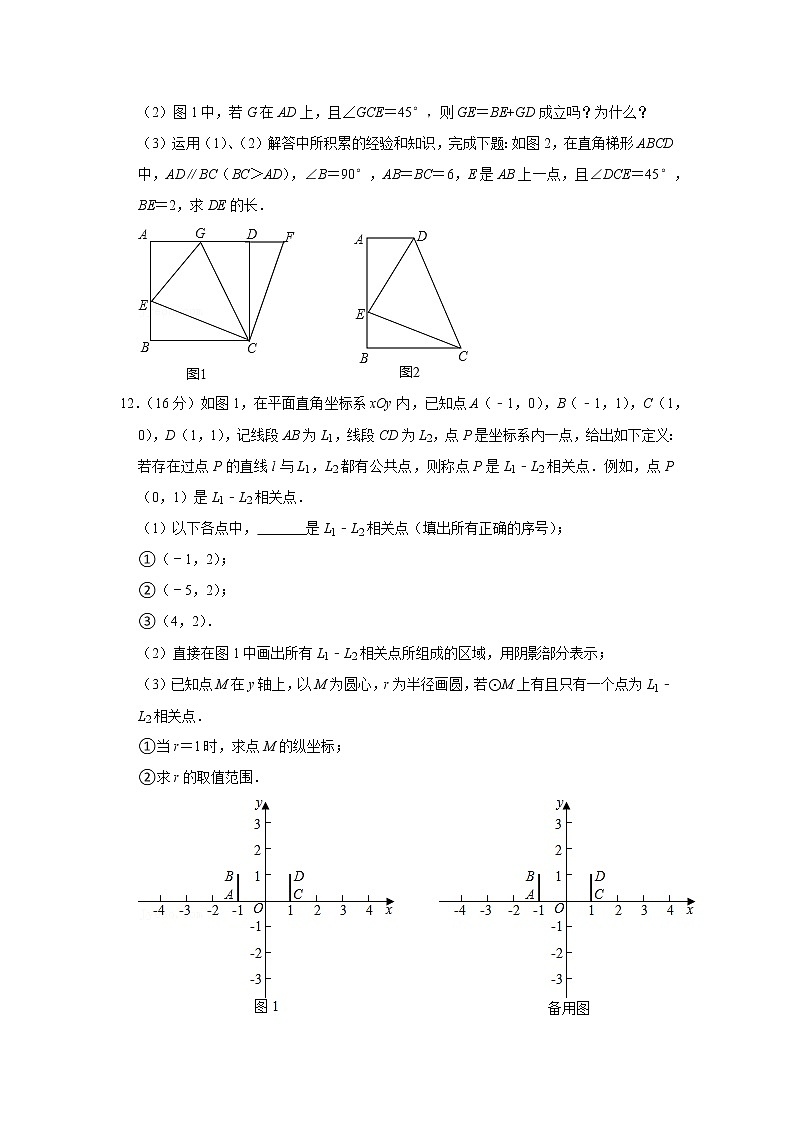
11.(16分)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是AB上一点,且∠DCE=45°,BE=2,求DE的长.
12.(16分)如图1,在平面直角坐标系xOy内,已知点A(﹣1,0),B(﹣1,1),C(1,0),D(1,1),记线段AB为L1,线段CD为L2,点P是坐标系内一点,给出如下定义:若存在过点P的直线l与L1,L2都有公共点,则称点P是L1﹣L2相关点.例如,点P(0,1)是L1﹣L2相关点.
(1)以下各点中, 是L1﹣L2相关点(填出所有正确的序号);
①(﹣1,2);
②(﹣5,2);
③(4,2).
(2)直接在图1中画出所有L1﹣L2相关点所组成的区域,用阴影部分表示;
(3)已知点M在y轴上,以M为圆心,r为半径画圆,若⊙M上有且只有一个点为L1﹣L2相关点.
①当r=1时,求点M的纵坐标;
②求r的取值范围.
13.(18分)定义:点P(x,y)为平面直角坐标系中的点,若满足x=y时,则称该点为“平衡点”,例如点(﹣1,﹣1),(0,0),(,),…都是“平衡点”.
(1)当﹣1≤x≤3时,直线y=2x+m上存在“平衡点”,则实数m的取值范围是 ;
(2)直线y=3mx+n﹣1上存在“平衡点”吗?若存在,请求出“平衡点”的坐标;若不存在,请说明理由;
(3)若抛物线y=ax2+bx+1(a>0)上存在两个不同的“平衡点”A(x1,x1),B(x2,x2),且满足0<x1<2,|x2﹣x1|=2,令=b2﹣2b+,试求实数t的取值范围.
2018年湖北省武汉市华中师大一附中高中招生数学试卷
参考答案与试题解析
一.选择题(本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,有且只有-项是正确的。)
1.(7分)二次函数y=x2+2x+c的图象与x轴的两个交点为A(x1,0),B(x2,0),且x1<x2,点P(m,n)是图象上一点,那么下列判断正确的是( )
A.当n>0时,m<x1 B.当n>0时,m>x2
C.当n<0时,m<0 D.当n<0时,x1<m<x2
【分析】根据题目中的函数解析式和二次函数的性质,可以判断各个选项中的结论是否正确,从而可以解答本题.
【解答】解:∵二次函数y=x2+2x+c,
∴该函数图象开口向上,
∵二次函数y=x2+2x+c的图象与x轴的两个交点为A(x1,0),B(x2,0),且x1<x2,点P(m,n)是图象上一点,
∴当n>0时,m<x1或m>x2,故选项A、B错误;
当n<0时,x1<m<x2,故选项C错误,选项D正确;
故选:D.
2.(7分)已知实数a、b、c满足a<b<c,并且k=++,则直线y=﹣kx+k一定经过( )
A.第一、三、四象限 B.第一、二、四象限
C.第一、二、三象限 D.第二、三、四象限
【分析】根据a<b<c,并且k=++,可以得到k的正负情况,然后根据一次函数的性质,即可得到直线y=﹣kx+k经过哪几个象限.
【解答】解:∵a<b<c,
∴c﹣a>b﹣a>0,
∴,
∵k=++,
∴k=++<++=<0,
∴直线y=﹣kx+k经过第一、三、四象限,
故选:A.
3.(7分)下边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图,若输入的a、b分别为16、22,则输出的a=(a←a﹣b的含义:将a﹣b的结果赋给a)( )
A.0 B.2 C.4 D.14
【分析】根据程序框图先判断,再执行,分别计算出当前的a、b的值,从而得到结论.
【解答】解:当a=16、b=22时,b=22﹣16=6,
当a=16、b=6时,a=16﹣6=10,
当a=10、b=6时,a=10﹣6=4,
当a=4、b=6时,b=6﹣4=2,
当a=4、b=2时,a=4﹣2=2=b,
故输出的a=2.
故选:B.
4.(7分)直线l:kx﹣y﹣2k﹣1=0被以A(1,0)为圆心,2为半径的⊙A所截得的最短弦长为( )
A. B.2 C.2 D.4
【分析】不论k取什么值,直线l一定经过定点,首先求得这个点的坐标,判断与圆的位置关系,然后利用垂径定理即可求.
【解答】解:kx﹣y﹣2k﹣1=0,
∴y=kx﹣2k﹣1=k(x﹣2)﹣1,
∴直线l一定经过点B(2,﹣1),
∵A(1,0),
∴AB=<2,
∴点B在⊙A的内部,当直线l⊥AB时,直线l截⊙A所得的弦最短,
∴最短的弦长为:2,
故选:C.
5.(7分)如图,△ABC中,AB=AC=8,BC=4,BF⊥AC于F,D是AB的中点,E为AC上一点,且2EF=AC,则tan∠DEF=( )
A. B. C. D.
【分析】通过作垂线,构造直角三角形,利用直角三角形的边角关系、勾股定理,以及相似三角形的性质求解即可.
【解答】解:过点A作AM⊥BC,垂足为M,过点D作DN⊥AC,垂足为N,
∵AB=AC=8,BC=4,
∴BM=MC=BC=2,
在Rt△AMC中,
AM===2,
又∵BF⊥AC,
∴∠BFC=∠AMC=90°,
又∵∠C=∠C,
∴△BFC∽△AMC,
∴====,
∴FC=1,BF=,
又∵2EF=AC=8,
∴EF=4,
∵D是AB的中点,DN∥BF,
∴DN=BF=,AN=NF=AF=(8﹣1)=,
∴EN=EC﹣NC=(4+1)﹣(+1)=,
在Rt△DEN中,
tan∠DEN==,
即tan∠DEF=.
故选:C.
二、填空题(本大题共5小题,每小题7分,共35分)
6.(7分)若a+b﹣2﹣4=3﹣c﹣5,则(b﹣c)a的值为 36 .
【分析】将a+b﹣2﹣4=3﹣c﹣5变形为a﹣1﹣2+1+b﹣2﹣4+4+(c﹣3﹣6+9)=0,配方后根据非负数的性质可求a,b,c,再代入计算即可求解.
【解答】解:∵a+b﹣2﹣4=3﹣c﹣5,
∴a﹣1﹣2+1+b﹣2﹣4+4+(c﹣3﹣6+9)=0,
即(﹣1)2+(﹣2)2+(﹣3)2=0,
∴﹣1=0,﹣2=0,﹣3=0,
解得a=2,b=6,c=12,
∴(b﹣c)a=(6﹣12)2=36.
故答案为:36.
7.(7分)已知△ABC的一边长为4,另外两边长恰是方程2x2﹣12x+m+1=0的两实根,则实数m的取值范围是 9<m≤17 .
【分析】根据一元二次方程的根与系数的关系及三角形的三边关系可得到(x1﹣x2)2<16,把两根之积与两根之和代入(x1﹣x2)2的变形中,可求得m的取值范围,再由根的判别式确定出m的最后取值范围.
【解答】解:由根与系数的关系可得:x1+x2=6,x1•x2=,
又有三角形的三边关系可得:|x1﹣x2|<4,
则(x1﹣x2)2<16,
即(x1+x2)2﹣4x1•x2<16,
即:36﹣2m﹣2<16,
解得:m>9;
既然方程有两个实根,则△≥0,
解得m≤17.
故答案为:9<m≤17.
8.(7分)点D是△ABC的边AB上的一点,使得AB=3AD,P是△ABC外接圆上一点,使得∠ADP=∠ACB,则的值为 .
【分析】连接AP,由圆周角定理可得出∠APB=∠ACB,进而可得出∠APB=∠ACB=∠ADP,由相似三角形的判定定理可得出△APB∽△ADP,再根据相似三角形的对应边成比例即可得出结论.
【解答】解:连接AP,
∵∠APB与∠ACB是所对的圆周角,
∴∠APB=∠ACB,
∵∠ADP=∠ACB,
∴∠APB=∠ACB=∠ADP,
∵∠DAP=∠DAP,
∴△APB∽△ADP,
∴==,
∴AP2=AD•AB=AD•(3AD)=3AD2,
∴===.
故答案为:.
9.(7分)有十张正面分别标有数字1,2,3,4,5,6,7,8,9,10的不透明卡片,它们除数字不同外其余全部相同,将它们背面朝上,洗匀后从中任取一张,以卡片上的数字作为关于x的不等式5x﹣a≤5中的系数a,使得该不等式的正整数解只有1和2的概率为 .
【分析】先解不等式得到x≤,再利用不等式的整数得到∴2≤<3,解得5≤a<10,然后根据概率公式求解.
【解答】解:解不等式5x﹣a≤5得x≤,
∵该不等式的正整数解只有1和2,
∴2≤<3,解得5≤a<10,
∵从10张中任取一张,取的数满足5≤a<10有5个,
∴洗匀后从中任取一张,以卡片上的数字作为关于x的不等式5x﹣a≤5中的系数a,使得该不等式的正整数解只有1和2的概率==.
故答案为.
10.(7分)若四个互不相等的正实数a,b,c,d满足(a2018﹣c2018)(a2018﹣d2018)=2018,(b2018﹣c2018)(b2018﹣d2018)=2018,则(ab)2018﹣(cd)2018的值为 ﹣2018 .
【分析】根据题意可将a2018与b2018看做方程(x﹣c2018)(x﹣d2028)=2018的两个解,把所求的式子被减数利用积的乘方逆运算变形后换为x1x2,把方程整理后,利用根与系数的关系表示出x1x2,代入整理后的式子中,即可求出所求式子的值.
【解答】解:设a2018与b2018看做方程(x﹣c2018)(x﹣d2018)=2018的两个解,
方程整理得:x2﹣(c2018+d2018)x+(cd)2018﹣2018=0,
则(ab)2018﹣(cd)2018=,
又x1x2=(cd)2018﹣2018,
则(ab)2018﹣(cd)2018==(cd)2018﹣2018﹣(cd)2018=﹣2018.
故答案为:﹣2018.
三、解答题(本大题共3小题,共50分解答应写出文字说明、证明过程和演算步骤.)
11.(16分)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是AB上一点,且∠DCE=45°,BE=2,求DE的长.
【分析】(1)根据正方形的性质可知:CB=CD,DF=BE,∠B=∠CDA,于是证得△CEB≌△CFD,即可证出CE=CF,
(2)首先证出∠ECF=90°,故可知∠FCG=45°,于是证得△CEG≌△CFG,即可证出GE=GF=DF+GD=BE+GD,
(3)首先求出DE=DF=DG+BE=DG+2=AB﹣AD+2=6﹣AD+2=8﹣AD,然后根据勾股定理的知识求出AD的值,进而求出DE的值.
【解答】(1)证明:∵四边形ABCD是正方形,
∴CB=CD,∠B=∠CDA,
∵DF=BE,
∴△CEB≌△CFD,
∴CE=CF,
(2)解:成立.理由如下:
过C作CG⊥DF,
证得∠ECF=90°,
∴∠FCG=45°,
证得△CEG≌△CFG(SAS),
∴GE=GF=DF+GD=BE+GD,
(3)解:延长AD到F,使得DF=DE,过C作CG⊥DF,
同理得:DE=DF=DG+BE=DG+2=AB﹣AD+2=6﹣AD+2=8﹣AD,
又∵DE=,
∴,
∴AD=3,
∴DE=5.
12.(16分)如图1,在平面直角坐标系xOy内,已知点A(﹣1,0),B(﹣1,1),C(1,0),D(1,1),记线段AB为L1,线段CD为L2,点P是坐标系内一点,给出如下定义:若存在过点P的直线l与L1,L2都有公共点,则称点P是L1﹣L2相关点.例如,点P(0,1)是L1﹣L2相关点.
(1)以下各点中, ②③ 是L1﹣L2相关点(填出所有正确的序号);
①(﹣1,2);
②(﹣5,2);
③(4,2).
(2)直接在图1中画出所有L1﹣L2相关点所组成的区域,用阴影部分表示;
(3)已知点M在y轴上,以M为圆心,r为半径画圆,若⊙M上有且只有一个点为L1﹣L2相关点.
①当r=1时,求点M的纵坐标;
②求r的取值范围.
【分析】(1)画出图象,根据L1﹣L2相关点定义判断即可;
(2)连接BD、BC、AD,即可得到所有L1﹣L2相关点所组成的区域;
(3)①画出图形,由M在y轴上,⊙M上只有一个点为L1﹣L2相关点,知⊙M与AC相切或⊙M与BD相切,即可得到M的坐标为(0,﹣1)或(0,2);
②画出图形,不妨设M位于阴影部分下方,则⊙M与AC相切于O(0,0),且⊙M与直线AD相离,过M作ME⊥AD于E,设AD与BC交于F,在Rt△AOF中,可得sin∠AFO==,在Rt△FEM中,ME=(+r)•,根据(+r)•>r,即可得r<2+,故r的取值范围是0<r<2+.
【解答】解:(1)如图:
由图可知,过(﹣5,2)、(4,2)都存在直线,与L1,L2都有公共点,而过(﹣1,2)不能作直线,使直线和L1,L2都有公共点,根据L1﹣L2相关点的定义,(﹣5,2)、(4,2)是L1﹣L2相关点,(﹣1,2)不是L1﹣L2相关点,
故答案为:②③;
(2)所有L1﹣L2相关点所组成的区域,用阴影部分表示如下(含边界):
(3)①如图:
∵M在y轴上,⊙M上只有一个点为L1﹣L2相关点,
∴⊙M与AC相切或⊙M与BD相切,
∵⊙M的半径r=1,
∴M(0,﹣1)或M'(0,2),
即⊙M上有且只有一个点为L1﹣L2相关点,M的坐标为(0,﹣1)或(0,2);
②阴影部分关于直线y=对称,故不妨设M位于阴影部分下方,如图:
∵点M在y轴上,⊙M上有且只有一个点为L1﹣L2相关点,阴影部分关于y轴对称,
∴⊙M与AC相切于O(0,0),且⊙M与直线AD相离,
过M作ME⊥AD于E,设AD与BC交于F,
∴MO=r,ME>r,F(0,),
在Rt△AOF中,∠AOF=90°,OA=1,OF=,
∴AF==,
∴sin∠AFO==,
在Rt△FEM中,FM=OF+OM=+r,
∴ME=FM•sin∠EFM=FM•sin∠AFO=(+r)•,
∴(+r)•>r,
解得r<2+,
∴r的取值范围是0<r<2+.
13.(18分)定义:点P(x,y)为平面直角坐标系中的点,若满足x=y时,则称该点为“平衡点”,例如点(﹣1,﹣1),(0,0),(,),…都是“平衡点”.
(1)当﹣1≤x≤3时,直线y=2x+m上存在“平衡点”,则实数m的取值范围是 ﹣3≤m≤1 ;
(2)直线y=3mx+n﹣1上存在“平衡点”吗?若存在,请求出“平衡点”的坐标;若不存在,请说明理由;
(3)若抛物线y=ax2+bx+1(a>0)上存在两个不同的“平衡点”A(x1,x1),B(x2,x2),且满足0<x1<2,|x2﹣x1|=2,令=b2﹣2b+,试求实数t的取值范围.
【分析】(1)根据x=y,﹣1≤x≤3可得出关于m的不等式,求出m的取值范围即可;
(2)联立方程,分三种情况讨论;
(3)先将A(x1,x1),B(x2,x2)代入y=ax2+bx+1,得到ax12+(b﹣1)x1+1=0,ax22+(b﹣1)x2+1=0,根据方程的解的定义可知x1,x2是一元二次方程ax2+(b﹣1)x+1=0的两个根,由根与系数的关系可得x1+x2=,x1•x2=,则(x1﹣x2)2=(x1+x2)2﹣4x1•x2==4,整理得出b2﹣2b=(2a+1)2﹣2,则t=b2﹣2b+=(2a+1)2+.再由﹣2<x1<2,|x1﹣x2|=2,得出﹣4<x2<4,﹣8<x1•x2<8,即﹣8<<8,又a>0,解不等式组得出a>,进而求出t的取值范围.
【解答】解:(1)∵x=y,
∴x=2x+m,即x=﹣m.
∵﹣1≤x≤3,
∴﹣1≤﹣m≤3,
∴﹣3≤m≤1,
故答案为:﹣3≤m≤1;
(2)若直线y=3mx+n﹣1上存在“平衡点”,
∴3mx+n﹣1=x,
∴(3m﹣1)x=1﹣n,
当3m﹣1=0,1﹣n=0,即m=,n=1,此时方程有无数个解,此时直线y=3mx+n﹣1上所有点都是“平衡点”,坐标为(x,x),x为任意实数;
当3m﹣1=0,1﹣n≠0,即m=,n≠1,此时方程无解,此时直线上不存在“平衡点”;
当3m﹣1≠0,即m≠,此时方程有唯一解为x=,此时直线上只有一个“平衡点”,坐标为(,);
(3)联立方程组可得:,
可得ax2+(b﹣1)x+1=0,
∵抛物线上存在两个不同的“平衡点”A(x1,x1),B(x2,x2),且满足0<x1<2,
∴x1+x2=,x1•x2=,△=(b﹣1)2﹣4a>0,
∴(x1﹣x2)2=(x1+x2)2﹣4x1•x2=()2﹣4•==4,
∴b2﹣2b=4a2+4a﹣1=(2a+1)2﹣2,
∴t=b2﹣2b+=(2a+1)2﹣2+=(2a+1)2+.
∵﹣2<x1<2,|x1﹣x2|=2,
∴﹣4<x2<0或0<x2<4,
∴﹣4<x2<4,
∴﹣8<x1•x2<8,
∴﹣8<<8,
∵a>0,
∴a>,
∴(2a+1)2+>+=2,
∴t>2.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/8/11 11:59:27;用户:节节高5;邮箱:5jiejg@xyh.com;学号:37675298
相关试卷
这是一份2020-2021学年湖北省武汉市华中师大一附中高一(上)期中数学试卷,共25页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年湖北省武汉市华中师大一附中高一(上)入学数学试卷,共25页。
这是一份2021-2022学年湖北省武汉市华中师大一附中高一(下)期中数学试卷(a卷),文件包含2021-2022学年湖北省武汉市华中师大一附中高一下期中数学试卷a卷docx、2021-2022学年湖北省武汉市华中师大一附中高一下期中数学试卷a卷pdf等2份试卷配套教学资源,其中试卷共58页, 欢迎下载使用。