

人教A版 (2019)选择性必修 第一册第一章 空间向量与立体几何本章综合与测试课后测评
展开
空间向量专题
一、选择题(本大题共3小题,共15.0分)
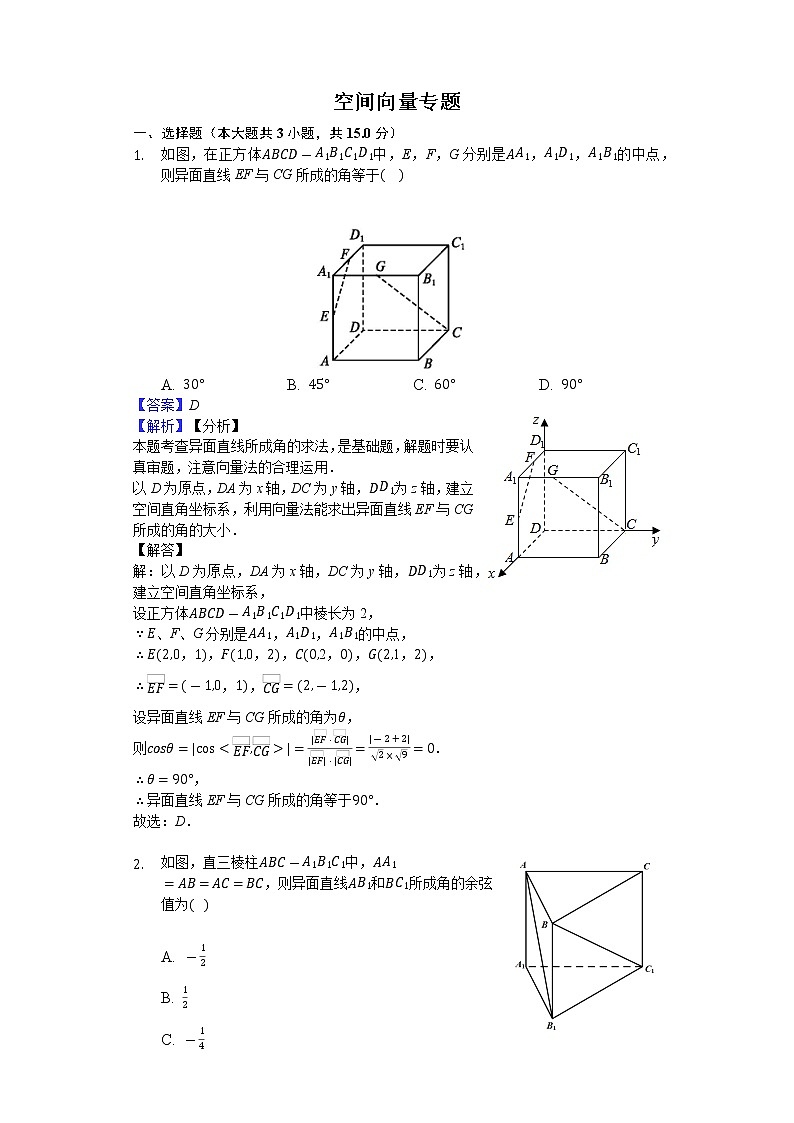
- 如图,在正方体中,E,F,G分别是,,的中点,则异面直线EF与CG所成的角等于
A. B. C. D.
【答案】D
【解析】【分析】
本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.
以D为原点,DA为x轴,DC为y轴,为z轴,建立空间直角坐标系,利用向量法能求出异面直线EF与CG所成的角的大小.
【解答】
解:以D为原点,DA为x轴,DC为y轴,为z轴,建立空间直角坐标系,
设正方体中棱长为2,
、F、G分别是,,的中点,
0,,0,,2,,1,,
0,,,
设异面直线EF与CG所成的角为,
则.
,
异面直线EF与CG所成的角等于.
故选:D.
- 如图,直三棱柱中,,则异面直线和所成角的余弦值为
A.
B.
C.
D.
|
【答案】D
【解析】【分析】
本题考查空间几何体中异面直线所成的角的问题,考查余弦定理的应用,属于中档题.分别取AB,,的中点D,E,F,连接DE,DF,则或其补角即为异面直线和所成的角.在三角形DEF中,根据余弦定理即可求出结果.
【解答】
解:分别取AB,,的中点D,E,F,连接DE,DF,EF.
则,
所以或其补角即为异面直线和所成的角.
不妨设,
则.
所以在三角形DEF中,,
所以异面直线和所成的角的余弦值为.
故选D.
- 如图,在直三棱柱中,,,,D,E分别是AB,的中点,则异面直线BE与CD所成的角的余弦值为
A.
B.
C.
D.
|
【答案】C
【解析】【分析】
本题考查异面直线所成的角,涉及余弦定理和勾股定理,属于中档题.
取的中点F,连结DF,EF,CF,得到,则就是异面直线BE与CD所成的角或其补角,进行求解即可.
【解答】
解:取的中点F,连结DF,EF,CF.
易知EF是的中位线,所以且1,
又且,所以且.
所以四边形EFDB是平行四边形,
所以,
所以就是异面直线BE与CD所成的角或其补角.
因为,,,D,E,F分别是AB,,的中点,
所以,且.
所以由勾股定理,得,
所以.
由勾股定理,得,
.
在中,由余弦定理得.
故选C.
二、解答题(本大题共9小题,共108.0分)
- 在直三棱柱中,底面是直角三角形,,D为侧棱的中点.
求异面直线,所成角的余弦值;
求二面角的平面角的余弦值.
【答案】解:由已知得CA,CB,两两垂直,
如图所示,以C为原点,CA,CB,为坐标轴,建立空间直角坐标系,
则0,,0,,2,,0,,
2,,0,.
所以0,,,
所以
,
即异面直线与所成角的余弦值为
因为2,,0,,0,,
所以,,
所以为平面的一个法向量.
因为,0,,
设平面的一个法向量为,y,.
由,得
令,则,,2,.
所以,.
由图可知二面角的平面角是锐角,
所以二面角的余弦值为.
【解析】本题主要考查利用空间向量解决几何体中的夹角问题,包括两条异面直线的夹角和两个平面的夹角,属于中档题.
以C为原点,CA,CB,为坐标轴,建立空间直角坐标系,写出要用的点的坐标,写出两个向量的方向向量,根据两个向量所成的角得到两条异面直线所成的角.
先求两个平面的法向量,根据两个法向量所成的角得到结果.
- 如图,在四棱锥中,平面ABCD,,,,N为AD的中点.
求异面直线PB与CD所成角的余弦值;
点M在线段PC上且满足,直线MN与平面PBC所成角的正弦值为,求实数的值.
【答案】解:因为平面ABCD,平面ABCD,所以,又因为,所以两两垂直.
以A为空间坐标原点建立如图所示的空间直角坐标系.
由,N为AD的中点,得,所以,设异面直线PB与CD所成的角的大小为,则.
所以异面直线PB与CD所成角的余弦值为 ;
设平面PBC的法向量,因为,
由得,取,得,所以.
因为,所以,
所以.
依题意,
化简得,
解得或,由于M在线段PC上,所以.
【解析】本题考查利用空间向量方法研究异面直线及直线与平面所成角,属中档题.
依题意,建立空间坐标系,求得的坐标,进而求得结果;
依题意,求出平面PBC的法向量,
求得,根据求解即可.
- 如图,已知多面体,,,均垂直于平面ABC,,,,.
Ⅰ证明:平面;
Ⅱ求直线与平面所成的角的正弦值.
【答案】方法一:
Ⅰ证明:由得,
所以,故.
由得,
由得,
由,得,所以,
故,
又,平面,平面,
因此平面;
Ⅱ解:如图,过点作,交直线于点D,连接AD.
由平面得,平面平面,且平面平面,
由得平面,
所以是与平面所成的角.
由得,
所以,又,故.
因此,直线与平面所成的角的正弦值是.
方法二:
Ⅰ如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的正半轴,建立空间直角坐标系.
由题意知各点坐标如下:
因此
由,得.
由,得.
又,平面,平面,
所以平面.
Ⅱ设直线与平面所成的角为.
由Ⅰ可知
设平面的法向量.
由,即可取.
所以.
因此,直线与平面所成的角的正弦值是.
【解析】本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力、逻辑推理能力和运算求解能力,属于中档题.
方法一:
Ⅰ利用勾股定理的逆定理证明,,从而可得平面;
Ⅱ由题意得到是与平面所成的角,求解即可.
方法二:
Ⅰ如图建立空间直角坐标系,得出相关点到坐标,计算,,利用向量才垂直条件可得结论;
Ⅱ设直线与平面所成的角为,,求出平面的法向量,可得即可.
- 如图所示,在直三棱柱中,点M在线段上
若求异面直线AM和所成角的余弦值;
若直线AM与平面所成角为,试确定点M的位置.
【答案】解:以C为坐标原点,分别以CA,CB,所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则0,,0,,0,,4,
因为,所以3,
所以0,,3,
所以,.
所以异面直线AM和所成角的余弦值为.
由0,,4,,0,,
知4,,0,
设平面的法向量为b,,
由,得
令,则,,
所以平面的一个法向量为1,
因为点M在线段上,
所以可设,
所以
因为直线AM与平面所成角为,
所以,.
由,,
得
,
解得或.
因为点M在线段上,
所以,
即点2,是线段的中点.
【解析】本题考查利用空间向量求异面直线所成的角,利用空间向量求线面角,属于中档题.
以C为坐标原点,分别以CA,CB,所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系,求出0,,3,,利用法向量求异面直线所成的角;
求出平面的一个法向量为1,,可设,所以,利用直线AM与平面所成角为,列出方程,求出x即可求解.
- 如图,正四棱柱中,,,点P是棱的中点.
求直线和平面所成角的正弦值;
求点到平面的距离.
【答案】解:以D为原点,DA,DC,所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系:
,,点P是棱的中点.
0,,0,,1,,1,,
0,,0,,1,,1,,
1,.
,
设平面的法向量为,
则有,令,可得,
故,
则直线和平面所成角的正弦值为.
由可知,直线和平面所成角的正弦值为,
则点到平面的距离.
【解析】本题考查利用空间向量求解线面之间的夹角,求解点到面的距离,属于中档题.
建立空间坐标系,得出各点的空间坐标,求解出平面的法向量,再利用空间向量的数量积公式即可求解;
由可得直线和平面所成角满足,利用直角三角形性质即可求解得点到平面的距离
- 如图,在四棱锥中,底面ABCD为直角梯形,,,侧面SAB为正三角形且平面底面ABCD,,E,F分别为SD,SB的中点.
证明:平面SAB;
求EC与平面FCD所成角的正弦值.
【答案】证明:如图,取AD中点M,连接EM,CM,
因为EM为中位线,
所以,
所以,
又,
所以且,
所以四边形ABCM为平行四边形,
所以,
,,
所以平面平面SAB,
因为平面EMC,平面SAB,
所以平面SAB.
不妨设,取AB中点O,过O作,
因为平面底面ABCD,,
所以,,
又因为三角形SAB为正三角形,
所以,,
故如图建立空间直角坐标系,可得,
2,,0,,2,,4,,所以,,,
设平面FCD的一个法向量为,则即可取,
则,.
【解析】本题考查线面平行的判定和直线与平面所成角,属于中等难度;
取AD中点M,连接EM,CM,先证平面平面SAB,
因为平面EMC,平面SAB,平面SAB.
建立空间直角坐标系,可得,设平面FCD的一个法向量为,即可求解;
- 如图,已知四边形ABCD是边长为2的菱形,,平面平面ABCD,,,.
求证:平面平面AEFC;
若四边形AEFC为直角梯形,且,求二面角的余弦值.
【答案】证明:因为四边形ABCD是菱形,
所以,
又因为平面ABCD,平面平面ABCD,平面平面,
所以平面AEFC,
因为平面BDE,
所以平面平面AEFC.
解:设,如图,连接FO,
因为,四边形AEFC为直角梯形,且,
所以可得四边形AEFO为矩形,,
因为平面AEFC,平面AEFC,
所以,
因为,BD,平面ABCD,,
所以平面ABCD,
所以平面ABCD,
因为平面ABCD,
所以,
因为O为BD中点,
所以,
又,.
所以≌.
过B作交FC于G,则,
所以为二面角的平面角,
在中,
所以,,
同理,
在中,,
故,
,
,
故,解得,则,
在中,,
所以二面角的余弦值为.
【解析】本题考查面面垂直的判定和求二面角的平面角,考查推理能力和计算能力,属于中档题.
通过求证平面AEFC即可求证平面平面AEFC;
利用为二面角的平面角即可求解.
- 已知正三棱柱中,,D是BC的中点.
Ⅰ求证:平面;
Ⅱ求锐二面角的余弦值.
【答案】Ⅰ证明:连结 ,
设 ,则M是 的中点,
再连结 DM,则 DM是 的中位线,
所以 ,
又因为平面 ,平面 ,
所以平面 ;
Ⅱ解:取AB的中点O, 的中点,连结和OC,易知两两垂直,以O为原点,建立如图所示的空间直角坐标系,
则有,,,,
所以,,
设平面的一个法向量,
则令,则有,,
所以,
同理可求平面的一个法向量
所以
又因为二面角是锐二面角,
所以锐二面角的余弦值为.
【解析】本题考查线面平行的判定,二面角,利用空间向量求线线、线面和面面的夹角,考查逻辑推理能力和空间想象能力,属于中档题.
Ⅰ连结 ,设 ,连结 DM,根据题意,证明,由线面平行的判定定理可得;
Ⅱ取AB的中点O, 的中点,连结和OC,易知两两垂直,以O为原点,建立空间直角坐标系,利用空间向量法计算可得.
- 如图所示,在四棱柱中,侧棱平面ABCD,底面ABCD是直角梯形,,.
证明:平面;
若,求二面角的正弦值.
【答案】解:因为侧棱平面ABCD,所以平面平面ABCD,
又,平面平面,所以平面,
而平面,所以;
因为侧棱平面ABCD,所以,又,所以,
又,所以平面.
如图,以D为坐标原点,分别以AD、DC、所在直线为x、y、z轴建立空间直角坐标系.
则0,,1,,4,,4,.
设平面的法向量为,又,,
则求得令,得.
设平面的法向量为,又,,
则求得令,得.
另解:由可得平面的法向量为,设为,
所以,
故二面角的正弦值为.
【解析】本题考查线面垂直的判定和二面角,属于中档题;
先证;再证,又,所以平面.
以D为坐标原点,分别以AD、DC、所在直线为x、y、z轴建立空间直角坐标系.则0,,1,,4,,4,可得平面的法向量为,平面的法向量为利用夹角公式即可求解;
人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示课后练习题: 这是一份人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示课后练习题,共9页。
选择性必修 第一册第一章 空间向量与立体几何1.4 空间向量的应用练习题: 这是一份选择性必修 第一册第一章 空间向量与立体几何1.4 空间向量的应用练习题,共14页。试卷主要包含了选择题,解答题,填空题等内容,欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用巩固练习: 这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用巩固练习,共18页。试卷主要包含了解答题等内容,欢迎下载使用。













