

高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用课堂检测
展开
空间向量所成角问题复习20道选择题
一、选择题(本大题共20小题,共100.0分)
- 已知两平面的法向量分别为1,,1,,则两平面所成的二面角为
A. B. C. 或 D.
- 设直线l的方向向量为,平面的法向量为,,则使成立的是
- ,1,
B. ,1,
C. 1,,
D. ,1,
- 设向量,,则,
A. B.
C. D.
- 若不重合的两个平面的法向量分别是,,则这两个平面的位置关系是
A. 平行 B. 垂直 C. 相交但不垂直 D. 不能确定
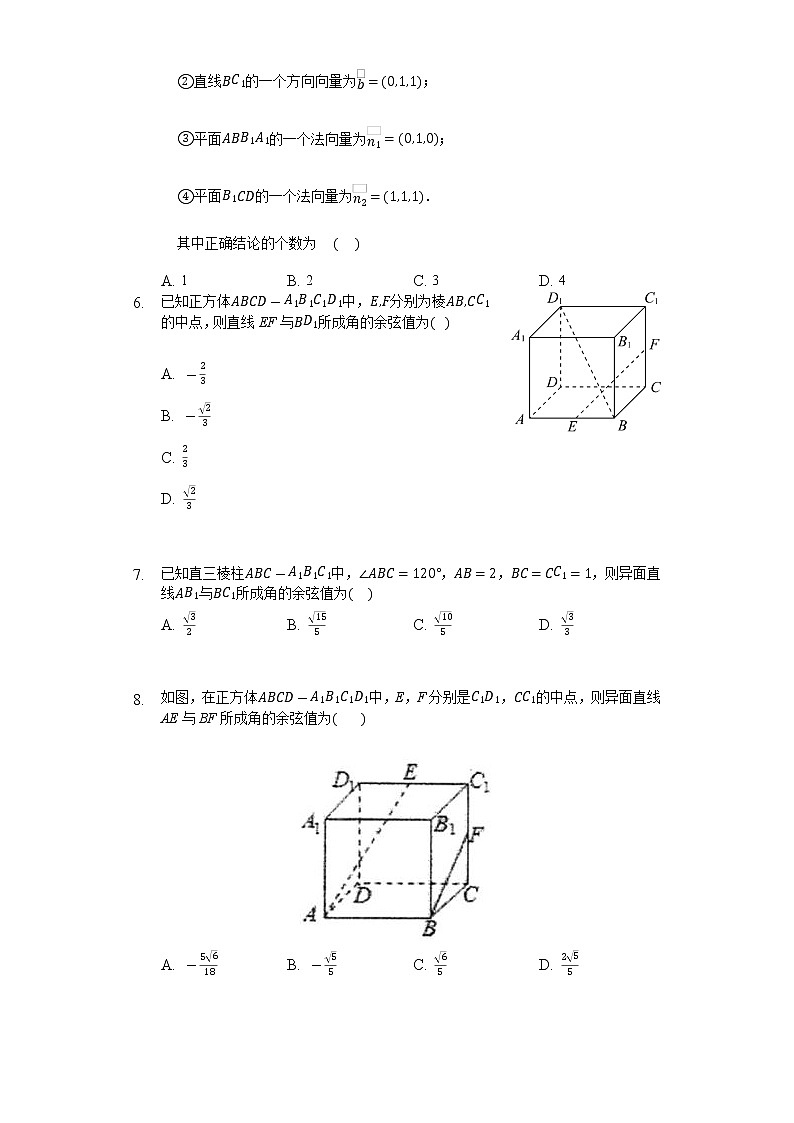
- 在如图所示的空间直角坐标系中,是棱长为1的正方体,给出下列结论:
直线的一个方向向量为;
直线的一个方向向量为;
平面的一个法向量为;
平面的一个法向量为.
其中正确结论的个数为
A. 1 B. 2 C. 3 D. 4
- 已知正方体中,分别为棱的中点,则直线EF与所成角的余弦值为
A.
B.
C.
D.
|
- 已知直三棱柱中,,,,则异面直线与所成角的余弦值为
A. B. C. D.
- 如图,在正方体中,E,F分别是,的中点,则异面直线AE与BF所成角的余弦值为
A. B. C. D.
- 已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为
A. B. C. D.
- 如图,在正方体中,直线与平面ABCD所成角的余弦值是
A. B. C. D.
- 如图,已知长方体中,,,则直线和平面所成角的正弦值等于
- B. C. D.
|
- 在正三棱柱中,侧棱长为,底面三角形的边长为1,则与侧面所成角的大小为
A.
B.
C.
D.
|
- 如图,在正方体中,下列结论不正确的是
A.
B.
C.
D.
|
- 将正方形ABCD沿对角线BD折成直二面角,有如下四个结论:
;
是等边三角形;
与平面BCD所成的角为;
与CD所成的角为.
其中错误的结论是
A. B. C. D.
- 如图,在正方体中,分别是的中点,则下列判断错误的是
- B.
C. D.
|
- 如图,在直三棱柱中,,,,D,E分别是,的中点,则直线DE与平面所成的角的正弦值为
- B. C. D.
|
- 如图,已知直三棱柱中,,,则直线与直线所成角的余弦值为
A. B. C. D.
- 已知正四棱柱的体积为,底面ABCD的边长为1,则二面角的余弦值为
A. B. C. D.
- 如图,四棱锥中,平面ABCD,四边形ABCD是正方形,,M是棱PC的中点,N是棱PB的中点,则异面直线AN,BM所成角的余弦值为
A. B. C. D. 0
- 已知两平面的法向量分别为1,,1,,则两平面所成的二面角为
A. B. C. 或 D.
空间向量所成角问题复习20道选择题
一、选择题(本大题共20小题,共100.0分)
- 已知两平面的法向量分别为1,,1,,则两平面所成的二面角为
A. B. C. 或 D.
【答案】C
【解析】【分析】
本题考查的知识点是二面角的平面角及求法,其中一定要注意两平面所成的二面角与,相等或互补.根据已知中两个平面法向量的夹角,代入向量夹角公式,可以求出两个向量的夹角,进而根据两平面所成的二面角与,相等或互补,得到答案.
【解答】
解:两平面的法向量分别为1,,1,,
则两平面所成的二面角与,相等或互补
,
故,
故两平面所成的二面角为或
故选C.
- 设直线l的方向向量为,平面的法向量为,,则使成立的是
A. ,1,
B. ,1,
C. 1,,
D. ,1,
【答案】B
【解析】解:直线l的方向向量为,平面的法向量为,,使
成立,
,
在A中,,故A错误;
在B中,,故B成立;
在C中,,故C错误;
在D中,,故D错误.
故选:B.
由直线l的方向向量为,平面的法向量为,,使成立,得到,由此能求出结果.
本题考查线面平行的判断与求法,考查直线的方向向量、平面的法向量等基础知识,考查运算与求解能力,考查化归与转化思想,是基础题.
- 设向量,,则,
A. B.
C. D.
【答案】D
【解析】【分析】
本题考查了空间向量的夹角三角函数值的求法,属于简单题.
利用即可求出.
【解答】
解:向量,,
.
故选D.
- 若不重合的两个平面的法向量分别是,,则这两个平面的位置关系是
A. 平行 B. 垂直 C. 相交但不垂直 D. 不能确定
【答案】B
【解析】【分析】
本题考查利用空间向量研究平面平行及垂直,同时考查空间向量平行的条件,属于基础题.
观察两个向量坐标的数量关系,判断向量平行或垂直即可.
【解答】
解:,,
,故两个向量垂直.
所以两个平面垂直.
故选B.
- 在如图所示的空间直角坐标系中,是棱长为1的正方体,给出下列结论:
直线的一个方向向量为;
直线的一个方向向量为;
平面的一个法向量为;
平面的一个法向量为.
其中正确结论的个数为
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】【分析】
本题考查了空间向量的应用、向量共线定理,考查了推理能力与计算能力,属于简单题.
直线l的方向向量与平面的法向量平行,再利用向量共线定理即可判断出结论.
【解答】
解:因为,,所以正确.
,,所以正确.
因为直线平面,,所以正确.
点的坐标为1,,与平面不垂直,错误.
故选C.
- 已知正方体中,分别为棱的中点,则直线EF与所成角的余弦值为
A.
B.
C.
D.
|
【答案】D
【解析】【分析】
本题在正方体中求两条异面直线所成角的余弦值,着重考查了利用空间坐标系求向量的长度和夹角等知识,属于基础题.
以AB、AD、为x、y、z轴,建立空间直角坐标系如图,可得B、、E、F各点的坐标,从而得到和的坐标,利用空间向量的夹角公式求出它们所成角的余弦,即可得到异面直线EF与所成角的余弦值.
【解答】
解:以AB、AD、为x、y、z轴,建立空间直角坐标系,取,
则0,,1,,0,,1,
1,,1,,
可得,,
,
设异面直线EF与所成角为,
则,
故选D.
- 已知直三棱柱中,,,,则异面直线与所成角的余弦值为
A. B. C. D.
【答案】C
【解析】【分析】
本题考查了空间中的两条异面直线所成角的计算问题,也考查了空间中的平行关系应用问题,是中档题.
设M、N、P分别为AB,和的中点,得出、夹角为MN和NP夹角或其补角;根据中位线定理,结合余弦定理求出AC、MQ,MP和的余弦值即可.
【解答】
解:如图所示,
设M、N、P分别为AB,和的中点,
则,,
则、夹角为MN和NP夹角或其补角因异面直线所成角为,
可知,;
作BC中点Q,则为直角三角形,,,
中,由余弦定理得
,
,,;
在中,由余弦定理得
;
又异面直线所成角的范围是,
与所成角的余弦值为.
故选C.
- 如图,在正方体中,E,F分别是,的中点,则异面直线AE与BF所成角的余弦值为
A. B. C. D.
【答案】D
【解析】【分析】
本题考查异面直线所成角的余弦值的求法,是基础题.
以D为原点,DA为x轴,DC为y轴,为z轴,建立空间直角坐标系,由此利用向量法能求出异面直线AE与BF所成角的余弦值.
【解答】
解:以D为原点,DA为x轴,DC为y轴,为z轴,建立空间直角坐标系,
设正方体棱长为2,E,F分别是,的中点,
0,,1,,2,,2,,
1,,0,,
设异面直线AE与BF所成角的平面角为,
则.
异面直线AE与BF所成角的余弦值为.
故选D.
- 已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为
A. B. C. D.
【答案】B
【解析】【分析】
本题考查异面直线及其所成的角,关键是找角,考查了余弦定理的应用,是中档题.
由E为AB的中点,可取AD中点F,连接EF,则为异面直线CE与BD所成角,设出正四面体的棱长,求出的三边长,然后利用余弦定理求解异面直线CE与BD所成角的余弦值.
【解答】
解:如图,
取AD中点F,连接EF,CF,
为AB的中点,
,
则为异面直线BD与CE所成的角,
为正四面体,E,F分别为AB,AD的中点,
.
设正四面体的棱长为2a,
则,
.
在中,由余弦定理得:
.
故选B.
- 如图,在正方体中,直线与平面ABCD所成角的余弦值是
A. B. C. D.
【答案】D
【解析】【分析】
本题考查了线面角的计算,考查计算能力,属于基础题.
连接AC,则为直线与平面ABCD所成的角,在中求出即可.
【解答】
解:连接AC,
平面ABCD,
为直线与平面ABCD所成的角,
设正方体的棱长为1,则,,
.
故选:D.
- 如图,已知长方体中,,,则直线和平面所成角的正弦值等于
A.
B.
C.
D.
|
【答案】C
【解析】【分析】
本题考查直线与平面所成的角,主要考查线面角,关键是寻找线面角,通常寻找斜线在平面上的射影,属于基础题.
要求线面角,先寻找斜线在平面上的射影,因此,要寻找平面的垂线,利用已知条件可得.
【解答】
解:由题意,连接,交于点O,
长方体中,,
,
又平面,,
,平面,平面,
平面,
直线和平面所成角为,
在中,,,.
即直线和平面所成角的正弦值等于.
故选C.
- 在正三棱柱中,侧棱长为,底面三角形的边长为1,则与侧面所成角的大小为
A.
B.
C.
D.
|
【答案】A
【解析】解:以C为原点,CA为x轴,在平面ABC中过C作AC的垂线为y轴,
为z轴,建立空间直角坐标系,
,0,,
,
平面的法向量1,,
设与侧面所成角的大小为,
则,
,
与侧面所成角的大小为.
故选:A.
以C为原点,CA为x轴,在平面ABC中过C作AC的垂线为y轴,为z轴,建立空间直角坐标系,利用向量法能求出与侧面所成角的大小.
本题考查线面角的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.
- 如图,在正方体中,下列结论不正确的是
A.
B.
C.
D.
|
【答案】C
【解析】【分析】
本题考查简单多面体棱柱、棱锥、棱台及其结构特征与空间中直线与直线的位置关系及利用空间向量判定线线的垂直平行关系的知识点,考查了正方体的结构特征,空间线线位置关系及其判定方法,属于基础题.
如图所示,建立空间直角坐标系,利用向量垂直与数量积的关系即可得出.
【解答】
解:如图所示,建立空间直角坐标系.
不妨设正方体的棱长.
则0,,1,,1,,1,,0,,
,0,,
,
,
因此不可能有,
故选C.
- 将正方形ABCD沿对角线BD折成直二面角,有如下四个结论:
;
是等边三角形;
与平面BCD所成的角为;
与CD所成的角为.
其中错误的结论是
A. B. C. D.
【答案】C
【解析】【分析】
本题考查的知识点是线面垂直的判定与性质,空间两点距离,线面夹角,异面直线的夹角,其中根据已知条件将正方形ABCD沿对角线BD折成直二面角,结合立体几何求出相关直线与直线、直线与平面的夹角,及线段的长是关键.
取BD的中点E,则,根据线面垂直的判定及性质可判断的真假;求出AC长后,可以判断的真假;求出AB与平面BCD所成的角可判断的真假;建立空间坐标系,利用向量法,求出AB与CD所成的角,可以判断的真假;进而得到答案.
【解答】
解:取BD的中点E,则,面AEC.
,故正确.
设正方形边长为a,则,.
.
为等边三角形,故正确.
为AB与面BCD所成的角为,故不正确.
以E为坐标原点,EC、ED、EA分别为x,y,z轴建立直角坐标系,
则0,,,,0,.
,.
,
,,故正确.
故选C.
- 如图,在正方体中,分别是的中点,则下列判断错误的是
A.
B.
C.
D.
|
【答案】D
【解析】【分析】
本题主要考查利用向量证明线面垂直,线面平行,线线垂直,线线平行,属于中档题.
利用向量法求解.
【解答】
解:如图,建立空间直角坐标系:
设正方体棱长为2,
则0,,2,,,
2,,,2,,1,,
则,,
,,
,,故A正确;
,,
,,
平面,故B正确;
根据,,
可知,MN和AB不平行,故MN和不平行,故D错误;
易求得平面ABCD法向量为,
则,又平面ABCD,
平面ABCD,故C正确;
故选D.
- 如图,在直三棱柱中,,,,D,E分别是,的中点,则直线DE与平面所成的角的正弦值为
A.
B.
C.
D.
|
【答案】A
【解析】【分析】
本题考查线面角的正弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.
以B为原点,分别以BC,BA,所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出直线DE与平面所成的角的正弦值.
【解答】
解:在直三棱柱中,且,,,
,即,
又平面ABC,
所以以B为原点,分别以BC,BA,所在直线为x,y,z轴,建立空间直角坐标系,
,E分别是,的中点,设,
,0,,,0,,
,
取平面的法向量1,,
设直线DE与平面所成的角为,
则
.
直线DE与平面所成的角的正弦值为.
故选A.
- 如图,已知直三棱柱中,,,则直线与直线所成角的余弦值为
A. B. C. D.
【答案】D
【解析】【分析】
本题考查利用空间向量求异面直线所成角,属于中档题.
设,建立的空间直角坐标系,得到向量,的坐标,即可求出,即可得出直线与直线夹角的余弦值.
【解答】
解:设,以C为原点,以CA,,CB分别为x轴,y轴,z轴,建立空间直角坐标系,如图所示:
所以0,,2,,0,,2,;
;
,
直线与直线夹角的余弦值为.
故选D.
- 已知正四棱柱的体积为,底面ABCD的边长为1,则二面角的余弦值为
A. B. C. D.
【答案】C
【解析】解:过D作于O,连接AO,
则就是二面角的平面角.
正四棱柱的体积为,底面ABCD的边长为1,.
在中,,,可得,.
在中,,
.
故选:C.
过D作于O,连接AO,则就是二面角的平面角.解即可.
本题考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养和向量法的合理运用.
- 如图,四棱锥中,平面ABCD,四边形ABCD是正方形,,M是棱PC的中点,N是棱PB的中点,则异面直线AN,BM所成角的余弦值为
A. B. C. D. 0
【答案】D
【解析】【分析】
本题主要考查利用空间向量求异面直线所成的角,属于中档题.
先根据线面平行的性质定理确定点N的位置,再建系利用空间向量即可求出异面直线AN,BM所成角的余弦值.
【解答】
解:因为平面ABCD,所以,,
又ABCD为正方形,
所以,
如图,以A为原点,以AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
设,则0,,0,,2,,0,,0,,1,,
设异面直线AN,BM所成角为,
则,
故选D.
- 已知两平面的法向量分别为1,,1,,则两平面所成的二面角为
A. B. C. 或 D.
【答案】C
【解析】【分析】
本题考查的知识点是二面角的平面角及求法,属于中档题.
根据已知中两个平面法向量的夹角,代入向量夹角公式,可以求出两个向量的夹角,进而根据两平面所成的二面角与,相等或互补,得到答案.
【解答】
解:两平面的法向量分别为1,,1,,
则两平面所成的二面角与,相等或互补,
,
故,
故两平面所成的二面角为或,
故选C.
高中数学人教B版 (2019)必修 第四册11.3.1 平行直线与异面直线课时练习: 这是一份高中数学人教B版 (2019)必修 第四册11.3.1 平行直线与异面直线课时练习,共16页。
人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示课后练习题: 这是一份人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示课后练习题,共9页。
选择性必修 第一册第一章 空间向量与立体几何1.4 空间向量的应用练习题: 这是一份选择性必修 第一册第一章 空间向量与立体几何1.4 空间向量的应用练习题,共14页。试卷主要包含了选择题,解答题,填空题等内容,欢迎下载使用。













