初中数学北师大版七年级上册1.1 生活中的立体图形同步达标检测题

这是一份初中数学北师大版七年级上册1.1 生活中的立体图形同步达标检测题，共36页。
生活中的对称轴2016-2020年成都数学七年级下学期常规版期末汇编
1. 如图，将长方形 ABCD 沿 EF 折叠，点 D 落在 AB 边上的 H 点处，点 C 落在点 G 处，若 ∠AEH=30∘，则 ∠EFC 等于 ∘．


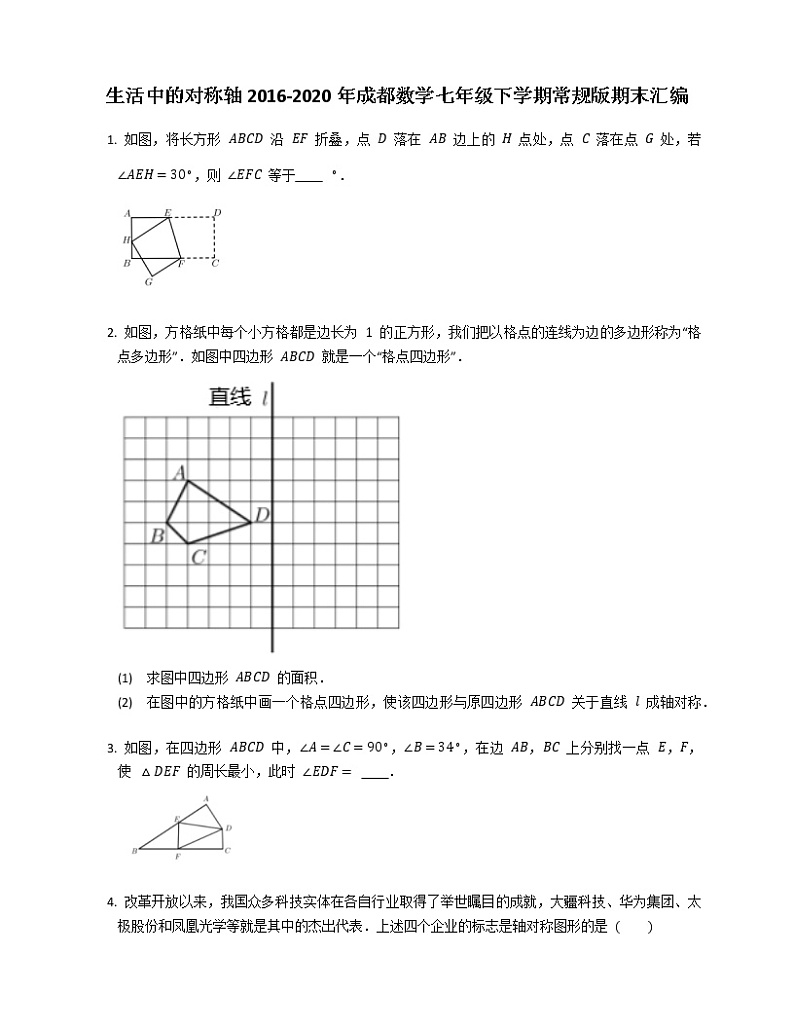
2. 如图，方格纸中每个小方格都是边长为 1 的正方形，我们把以格点的连线为边的多边形称为“格点多边形”．如图中四边形 ABCD 就是一个“格点四边形”．

(1) 求图中四边形 ABCD 的面积．
(2) 在图中的方格纸中画一个格点四边形，使该四边形与原四边形 ABCD 关于直线 l 成轴对称．

3. 如图，在四边形 ABCD 中，∠A=∠C=90∘，∠B=34∘，在边 AB，BC 上分别找一点 E，F，使 △DEF 的周长最小，此时 ∠EDF= ．


4. 改革开放以来，我国众多科技实体在各自行业取得了举世瞩目的成就，大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表．上述四个企业的标志是轴对称图形的是 (  )
A． B．
C． D．

5. 下列图形是我国国产品牌汽车的标识，其中是轴对称图形的是   
A． B．
C． D．

6. 如图，在边长为 1 的小正方形组成的网格中，四边形 ABCD 的四个顶点均在格点上．请按要求完成下列各题：

(1) 在网格中画出四边形 ABCD 关于直线 l 对称的四边形 A1B1C1D1．
(2) 求四边形 ABCD 的面积．

7. 下列四个手机APP图标中，是轴对称图形的是   
A． B． C． D．

8. 如图，在长度为 1 个单位长度的小正方形组成的正方形网格中，点 A，B，C 在小正方形的顶点上．

(1) 在图中画出 △ABC 关于直线 l 成轴对称的 △AʹBʹCʹ；
(2) 求 △ABC 的面积；
(3) 在直线 l 上找一点 P，使 PB+PC 的长最短，标出点 P（保留作图痕迹）．

9. 下面图形表示绿色食品、节水、节能和低碳四个标志，其中是轴对称图形的是   
A． B．
C． D．

10. 如图，在长度为 1 个单位长度的小正方形组成的正方形网格中，△ABC 的三个顶点 A，B，C 都在格点上．

(1) 在图中画出与 △ABC 关于直线 l 成轴对称的 △A1B1C1；
(2) 在直线 l 上找出一点 P，使得 ∣PA−PC∣ 的值最大；（保留作图痕迹并标上字母 P）
(3) 在直线 l 上找出一点 Q，使得 QA+QC1 的值最小；（保留作图痕迹并标上字母 Q）
(4) 在正方形网格中存在 个格点，使得该格点与 B，C 两点构成以 BC 为底边的等腰三角形．

11. 如图，将一张三角形纸片 ABC 的一角折叠，使点 A 落在 △ABC 外的 Aʹ 处，折痕为 DE．如果 ∠A=α，∠CEAʹ=β，∠BDAʹ=γ，那么 α，β，γ 三个角的关系是 ．


12. 四边形 ABCD 中，∠BAD=125∘，∠B=∠D=90∘，在 BC，CD 上分别找一点 M，N，当三角形 AMN 周长最小时，∠MAN 的度数为 ．


13. 下列标志中，可以看作是轴对称图形的是   
A． B． C． D．

14. 如图，正方形网格中每个小正方形边长都是 1．

(1) 画出 △ABC 关于直线 l 对称的图形 △A1B1C1；
(2) 在直线 l 上找一点 P，使 PB=PC；（要求在直线 l 上标出点 P 的位置)）
(3) 连接 PA，PC，计算四边形 PABC 的面积．

15. 新冠疫情发生以来，各地根据教育部“停课不停教，停课不停学”的相关通知精神，积极开展线上教学．下列在线学习平台的图标中，是轴对称图形的是   
A． B． C． D．

16. 下列标志中，可以看作是轴对称图形的是   
A． B． C． D．

17. 如图，把一张长方形纸片 ABCD 沿 EF 折叠，若 ∠EFG=50∘，则 ∠BGE=   

A． 100∘ B． 90∘ C． 80∘ D． 70∘

18. 如图，方格纸中每个小方格都是边长为 1 的正方形，四边形 ABCD 的顶点与点 E 都是格点．

(1) 作出四边形 ABCD 关于直线 AC 对称的四边形 ABʹCDʹ；
(2) 求四边形 ABCD 的面积；
(3) 若在直线 AC 上有一点 P，使得 P 到 D，E 的距离之和最小，请作出点 P (请保留作图痕迹)，且求出 PC= ．

19. 下列图形是中国一些航空公司的标志，其中是轴对称图形的是   
A． B． C． D．

20. 下面的四个汉字可以看作是轴对称图形的是   
A． B． C． D．

21. 如图，将长方形 ABCD 沿 EF 折叠，点 D 落在 AB 边上的 H 点处，点 C 落在点 G 处，若 ∠AEH=30∘，则 ∠EFC 等于 ∘．


22. 如图，方格纸中每个小方格都是边长为 1 的正方形，我们把以格点的连线为边的多边形称为“格点多边形”．如图中四边形 ABCD 就是一个“格点四边形”．

(1) 求图中四边形 ABCD 的面积；
(2) 在图中的方格纸中画一个格点四边形，使该四边形与原四边形 ABCD 关于直线 l 成轴对称．

23. 如图，在四边形 ABCD 中，∠A=∠C=90∘，∠B=34∘，在边 AB，BC 上分别找一点 E，F，使 △DEF 的周长最小，此时 ∠EDF= ．


24. 改革开放以来，我国众多科技实体在各自行业取得了举世瞩目的成就，大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表．上述四个企业的标志是轴对称图形的是   
A． B． C． D．

25. 如图，在边长为 1 的小正方形组成的网格中，点 A，B，C 均在小正方形的顶点上．

(1) 在图中画出与 △ABC 关于直线 l 成轴对称的 △AʹBʹCʹ；
(2) 求 △ABC 的面积．

26. 下列艺术字中，可以看作是轴对称图形的是   
A． B． C． D．

27. 如图有一张直角三角形纸片，两直角边 AC=4 cm，BC=8 cm，把纸片的部分折叠，使点 B 与点 A 重合，折痕为 DE，则 △ACD 的周长为 ．


28. 如图 a 是长方形纸带，∠DEF=15∘，将纸带沿 EF 折叠成图 b，则 ∠AEG 的度数 度，再沿 BF 折叠成图 c．则图中的 ∠CFE 的度数是 度．


29. 下面四个手机应用图标中是轴对称图形的是   
A． B． C． D．

30. 一个不透明的盒子中装有 4 张卡片，这 4 张卡片的正面分别画有等腰三角形、线段、圆和三角形，这些卡片除图形外都相同，将卡片搅匀．从盒子中任意抽取一张，卡片上的图形是轴对称图形的概率是 ．

31. 如图，方格图中每个小正方形的边长为 1，点 A，B，C 都是格点．

(1) 画出 △ABC 关于直线 MN 的对称图形 △AʹBʹCʹ；
(2) 直接写出线段 BBʹ 的长度；
(3) 直接写出 △ABC 的面积．

32. 下列图形中，是轴对称图形的是   
A． B． C． D．

33. 如图，方格纸中每个小方格都是边长为 1 的正方形，我们把顶点均在格点上的三角形称为“格点三角形”，如图 1，△ABC 就是一个格点三角形．（提示：作图时，先用 2B 铅笔作图，确定不再修改后用中性笔描黑）

(1) 作出 △ABC 关于直线 m 成轴对称的图形；
(2) 求 △ABC 的面积；
(3) 在图 2 的直线 m 上求作点 D，使得以 A，C，D 为顶点的格点三角形是等腰三角形．


34. 中国的方块字中有些具有对称性．下列美术字是轴对称图形的是   
A．爱 B．我 C．中 D．华

35. 如图，在 △ABC 中，AB=AC，∠C=70∘，△ABʹCʹ 与 △ABC 关于直线 AD 对称，∠CAD=10∘，连接 BBʹ，则 ∠ABBʹ 的度数是   

A． 45∘ B． 40∘ C． 35∘ D． 30∘

36. 如图，在 4×4 正方形网格中，黑色部分的图形构成一个轴对称图形，现在任选取一个白色的小正方形并涂黑，使图中黑色部分的图形仍然构成一个轴对称图形的概率是 ．


37. 图书馆的标志浓缩了图书馆的文化，下列图书馆标志中，是轴对称图形的是   
A． B．
C． D．

38. 如图，现有若干个边长相等的小等边三角形组成的图形，其中已经涂黑了 3 个小三角形（阴影部分表示），在空白的三角形中只涂黑一个小三角形，使整个图案成轴对称图形的概率是   

A． 19 B． 29 C． 13 D． 49

39. 如图 1，在正方形 ABCD 中，∠GAH=45∘，∠GAH 的两边分别与线段 BC，CD 相交于 E，F（点 E 不与 B，C 重合；点 F 不与 C，D 重合）．

(1) 填空：线段 BE，EF，DF 的数量关系是 ．
(2) 如图 2，点 P 是 EF 的中点，连接 AP，作点 E 关于直线 AB 的对称点 Eʹ，作点 F 关于直线 AD 的对称点 Fʹ，连接 EʹFʹ，求证：EʹFʹ=2AP．

(3) 如图 3，若 E，F 是 BC，CD 上的定点，利用（1），（2）的结论探究：当 AP=m，BE+DF=n 时，在线段 AB，AD 上是否分别存在 M，N，使四边形 MEFN 的周长有最小值，若存在，请求出最小值；若不存在，请说明理由．（用 m，n 的代数式表示）


40. 下列图形不是轴对称图形的是
A． B． C． D．

41. 下列大学的校徽图案是轴对称图形的是   
A． B．
C． D．

42. 如图，直线 l 是一条河，A，B 是两个新农村定居点．欲在 l 上的某点处修建一个水泵站，直接向 A，B 两地供水．现有如下四种管道铺设方案，图中实线表示铺设的供水管道，则铺设管道最短的方案是   

A． B． C． D．

43. 如图所示，△ABC 中，AB=6，AC=8，沿过 B 点的直线折叠这个三角形，使点 A 落在 BC 边上的点 E 处，折痕为 BD．若 △CDE 的周长为 11，则 BC 长为 ．


44. 下面的方格图是由边长为 1 的 42 个小正方形拼成的，△ABC 的顶点 A，B，C 均在小正方形的顶点上．

(1) 作出 △ABC 关于直线 m 对称的 △AʹBʹCʹ；
(2) 求 △ABC 的面积．

45. 下列图形中是轴对称图形的是   
A． B． C． D．

46. 如图，在长度为 1 个单位的小正方形组成的网格中，点 A，B，C 小正方形的顶点上．

(1) 在图中画出与 △ABC 关于直线 l 成轴对称的 △AʹBʹCʹ．
(2) △ABC 的面积为 ．
(3) 在直线 l 上找一点 P，使 PB+PC 的长最短，（在图形中标出点 P）

47. 下列图形中，为轴对称图形的是   
A． B．
C． D．

48. 如图，在正方形网格上有一个 △ABC．

(1) 画 △ABC 关于直线 MN 的对称图形（不写画法）；
(2) 若网格上的每个小正方形的边长为 1，求 △ABC 的面积．

49. 如图所示的五角星是轴对称图形，它的对称轴共有   

A． 1 条 B． 3 条 C． 5 条 D．无数条

50. 图①是一张长方形纸条，点 E，F 分别在 AD，BC 上，将纸条沿 EF 折叠成图②．再沿 BF 折叠成图③．若图③中的 ∠CFE=108∘，则图①中的 ∠DEF 的度数是 ．


51. 下列图形中，是轴对称图形的是   
A． B． C． D．

52. 如图，在 △ABC 中，D，E 分别是边 AB，AC 的中点，∠B=70∘，现将 △ADE 沿 DE 翻折，点 A 的对应点 M 刚好落在 BC 边上，则 ∠BDM 的大小是   

A． 70∘ B． 40∘ C． 30∘ D． 20∘

53. 将一等腰直角三角形纸片对折后再对折，得到如图所示的图形，然后将阴影部分剪掉，把剩余部分展开后的平面图形是   

A． B． C． D．

54. 观察下面的图形，其中是轴对称图形的是
A． B． C． D．

55. 如图，在边长为 1 的小正方形组成的网格中，给出了四边形 ABCD 的两条边 AB 与 BC，且四边形 ABCD 是一个轴对称图形，其对称轴为直线 AC．

(1) 在图中标出点 D，并画出该四边形的另两条边；
(2) 请直接写出四边形 ABCD 的面积．

56. 下列交通标志是轴对称图形的是   
A． B． C． D．

57. 下列图形中，是轴对称图形的是   
A． B．
C． D．

58. 下面四个手机应用图标中是轴对称图形的是   
A． B． C． D．

59. 如图，已知 △ABC 为等腰直角三角形，∠ACB 为直角，AC=BC=4，∠BCD=15∘，P 为射线 CD 上的动点，则 PA−PB 的最大值为 ．


60. 观察下面的图形，其中不是轴对称图形的是   
A． B． C． D．

61. 如图，下列 4×4 网格图都是由 16 个相同小正方形组成，每个网格图中有 4 个小正方形已涂上阴影，请在每图的空白小正方形中选取 3 个空白小正方形涂上阴影，使 7 个阴影小正方形组成一个轴对称图形，要求完成 3 种不同的涂法．


62. 如图，点 P 是 ∠AOB 内任意一点，OP=3，点 M 和点 N 分别是射线 OA 和射线 OB 上的动点，若 ∠AOB=30∘，则 △PMN 周长的最小值是 ．


63. 下面图形表示绿色食品、节水、节能和低碳四个标志，其中是轴对称图形的是   
A． B． C． D．

64. 如图，在长度为 1 个单位长度的小正方形组成的正方形网格中，△ABC 的三个顶点 A，B，C 都在格点上．

(1) 在图中画出与 △ABC 关于直线 l 成轴对称的 △A1B1C1．
(2) 在直线 l 上找出一点 P，使得 PA+PC1 的值最小．（保留作图痕迹并标上字母 P）
(3) 在正方形网格中存在 个格点，使得该格点与 B，C 两点构成以 BC 为底边的等腰三角形．

65. 如图，将一张三角形纸片 ABC 的一角折叠，使点 A 落在 △ABC 外的 Aʹ 处，折痕为 DE．如果 ∠A=α，∠CEAʹ=β，∠BDAʹ=γ，那么 α，β，γ 之间的关系是 ．


66. 如图，四边形 ABCD 中，∠BAD=125∘，∠B=∠D=90∘，在 BC，CD 上分别找一点 M，N，当三角形 AMN 周长最小时，∠MAN 的度数为 ．


67. 低碳环保的理念深入人心，共享单车已成为人们出行的重要工具．下列共享单车图标（不考虑颜色）中，是轴对称图形的有    个．

A． 0 B． 1 C． 2 D． 3

68. 如图，方格纸中每个小方格都是边长为 1 的正方形，四边形 ABCD 的顶点与点 E 都是格点．

(1) 作出四边形 ABCD 关于直线 AC 对称的四边形 ABʹCDʹ；
(2) 求四边形 ABCD 的面积；
(3) 若在直线 AC 上有一点 P，使得 P 到 D，E 的距离之和最小，请作出点 P（请保留作图痕迹），且求出 PC= ．

69. 图 1 为五边形纸片 ABCDE；如图 2，将 ∠A 以 BE 为折痕往下折，A 点恰好落在 CD 上；如图 3 再分别以 AB，AE 为折痕，将 ∠C 与 ∠D 往上折，使得 A，B，C，D，E 五点均在同一平面上，若图 3 中 ∠CAD=54∘，则图 1 中 ∠A 的度数为 ．


70. 下列手机软件图标中，是轴对称图形的是   
A． B．
C． D．

71. 下面有 4 个汽车标志图案，其中不是轴对称图形的是   
A． B．
C． D．

72. 下列图形中，不是轴对称图形的是   
A． B． C． D．

73. 如图，将纸片 △ABC 沿 DE 折叠，点 A 落在点 F 处，已知 ∠1+∠2=110∘，则 ∠A= 度．


74.
(1) 画 △ABC 关于直线 MN 的对称图形（对应，不写画法）；

(2) 若网格上的每个小正方形的边长为 1，求 △ABC 的面积．
答案
1. 【答案】 105
【解析】由折叠的性质可知：∠DEF=∠HEF，
∵∠AEH=30∘，
∴∠DEF=∠HEF=12180∘−∠AEH=75∘，
∴∠AEF=∠AEH+∠HEF=30∘+75∘=105∘，
∵ 四边形 ABCD 是长方形，
∴AD∥BC，
∴∠EFC=∠AEF=105∘．

2. 【答案】
(1) S四边形ABCD=12×3×1+12×3×3=32+92=6.
(2) 如图所示，四边形 AʹBʹCʹDʹ 即为所求．

3. 【答案】 112°
【解析】如图，作点 D 关于 BA 的对称点 P，点 D 关于 BC 的对称点 Q，连接 PQ，交 AB 于 E，交 BC 于 F，则点 E，F 即为所求，
∵ 四边形 ABCD 中，∠A=∠C=90∘，∠B=34∘，
∴∠ADC=180∘−34∘=146∘，
由轴对称知，∠ADE=∠P，∠CDF=∠Q，
在 △PDQ 中 ∠P+∠Q−∠ADC=180∘−146∘=34∘，
∴∠AED+∠CDF=∠P+∠Q=34∘，
∴∠EDF=∠ADC−∠ADE+∠CDF=180∘−34∘−34∘=112∘．


4. 【答案】B

5. 【答案】D

6. 【答案】
(1)
(2) 由（1）可知：
S四边形ABCD=S△ABC+S△ADC=12×5×2+12×5×1=152.

7. 【答案】B

8. 【答案】
(1) 如图，△AʹBʹCʹ 为所作；
(2) △ABC的面积=2×4−12×2×2−12×2×1−12×4×1=3.
(3) 如上图，点 P 为所作．

9. 【答案】A

10. 【答案】
(1) △A1B1C1 如图所示，
由对称的性质，分别作出 A，B，C 的对应点 A1，B1，C1，顺次连接 A1B1，A1C1，B1C1，得到 △A1B1C1 与 △ABC 关于直线 l 成轴对称．
(2) ∵C 与 C1 关于直线 l 对称，
∴PC=PC1．
∴∣PA−PC∣=∣PA−PC1∣，
当 P，A，C1 三点共线时，∣PA−PC1∣ 取得最大值，即 ∣PA−PC∣ 的值最大．
∴ 连接 AC1，延长 AC1 交直线 l 于点 P，点 P 即所求．
(3) ∵C 与 C1 关于直线 l 对称，
∴QC=QC1，
∴QA+QC1=QA+QC，
当 A，Q，C 三点共线时，QA+QC 取得最小值，即 QA+QC1 的值最小．
∴ 直线 AC 与直线 l 的交点 Q 即为所求．
(4) 4
【解析】
(4) ∵ 构成以 BC 为底边的等腰三角形，
则等腰三角形的顶点在线段 BC 的垂直平分线上．
∴ 作线段 BC 的垂直平分线，如图 D1，D2，D3，D4 即为所求，共 4 个格点．

11. 【答案】 γ=2α+β
【解析】由折叠得：∠A=∠Aʹ，
∵∠BDAʹ=∠A+∠AFD，∠AFD=∠Aʹ+∠CEAʹ，
∵∠A=α，∠CEAʹ=β，∠BDAʹ=γ，
∴∠BDAʹ=γ=α+α+β=2α+β，
故答案为：γ=2α+β．


12. 【答案】 70∘
【解析】延长 AB 到 Aʹ 使得 BAʹ=AB，延长 AD 到 Aʺ 使得 DAʺ=AD，连接 AʹAʺ 与 BC，CD 分别交于点 M，N．
∵∠ABC=∠ADC=90∘，
∴A，Aʹ 关于 BC 对称，Aʹ，Aʺ 关于 CD 对称，此时 △AMN 的周长最小，
∵BA=BAʹ，MB⊥AB，
∴MA=MAʹ，同理：NA=NAʺ，
∴∠Aʹ=∠MAB，∠Aʺ=∠NAD，
∵∠AMN=∠Aʹ+∠MAB=2∠Aʹ，∠ANM=∠Aʺ+∠NAD=2∠Aʺ，
∴∠AMN+∠ANM=2∠Aʹ+∠Aʺ，
∵∠BAD=125∘，
∴∠Aʹ+∠Aʺ=180∘−∠BAD=55∘，
∴∠AMN+∠ANM=2×55∘=110∘．
∴∠MAN=180∘−110∘=70∘．


13. 【答案】C
【解析】A、是中心对称图形，故A错误；
B、是中心对称图形，故B错误；
C、是轴对称图形，故C正确；
D、是中心对称图形，故D错误．

14. 【答案】
(1) 所作图形如图所示：
(2) 如图所示，过 BC 中点 D 作 DP⊥BC 交直线 l 于点 P，
此时 PB=PC．
(3) S四边形PABC=S△ABC+S△APC=12×5×2+12×5×1=152.

15. 【答案】A

16. 【答案】C
【解析】A、是中心对称图形，故A错误；
B、是中心对称图形，故B错误；
C、是轴对称图形，故C正确；
D、是中心对称图形，故D错误．

17. 【答案】A
【解析】 ∵ 四边形纸片 ABCD 是矩形纸片，
∴AD∥BC，
∴∠DEF=∠EFG，
又 ∵∠EFG=50∘，
∴∠DEF=50∘，
∵ 四边形 EFCʹDʹ 由四边形 EFCD 翻折而成，
∴∠GEF=∠DEF=50∘，
∴∠EGB=50∘+50∘=100∘，
故选：A

18. 【答案】
(1) 四边形 ABʹCDʹ 如图所示；
(2) S四边形ABCD=12×6×3=9．
(3) 5
【解析】
(3) 作点 E 关于直线 AC 的对称点 Eʹ，连接 DEʹ 交直线 AC 于 P，点 P 即为所求，此时 PC=5．

19. 【答案】D
【解析】A、不是轴对称图形，故本选项不符合题意；
B、不是轴对称图形，故本选项不符合题意；
C、不是轴对称图形，故本选项不符合题意；
D、是轴对称图形，故本选项符合题意．

20. 【答案】A
【解析】四个汉字中，可以看作轴对称图形的是．

21. 【答案】 105
【解析】 ∵ 将长方形 ABCD 沿 EF 折叠，点 D 落在 AB 边上的 H 点处，点 C 落在点 G 处，
∴∠DEF=∠HEF，
∵∠AEH=30∘，
∴∠DEF=∠HEF=12180∘−∠AEH=75∘，
∵ 四边形 ABCD 是长方形，
∴AD∥BC，
∴∠DEF+∠EFC=180∘，
∴∠EFC=180∘−75∘=105∘．

22. 【答案】
(1) S四边形ABCD=12×3×4=6．
(2) 如图，四边形 AʹBʹCʹDʹ 即为所求．

23. 【答案】 112°
【解析】如图，作点 D 关于 BA 的对称点 P，点 D 关于 BC 的对称点 Q，连接 PQ，交 AB 于 Eʹ，交 BC 于 Fʹ，则点 Eʹ，Fʹ 即为所求．
∵ 四边形 ABCD 中，∠A=∠C=90∘，∠B=α，
∴∠ADC=180∘−α，
由轴对称知，∠ADEʹ=∠P，∠CDFʹ=∠Q，
在 △PDQ 中，
∠P+∠Q=180∘−∠ADC=180∘−180∘−34∘=34∘,
∴∠ADEʹ+∠CDFʹ=∠P+∠Q=34∘，
∴∠EʹDFʹ=∠ADC−∠ADEʹ+∠CDFʹ=180∘−68∘=112∘．


24. 【答案】B
【解析】A、不是轴对称图形，故本选项错误；
B、是轴对称图形，故本选项正确；
C、不是轴对称图形，故本选项错误；
D、不是轴对称图形，故本选项错误．

25. 【答案】
(1) 如图，△AʹBʹCʹ 即为所求．
(2) △ABC 的面积
=2×4−12×1×2−12×1×3−12×1×4=72.

26. 【答案】B
【解析】A、不是轴对称图形，故本选项不合题意；
B、是轴对称图形，故本选项符合题意；
C、不是轴对称图形，故本选项不合题意；
D、不是轴对称图形，故本选项不合题意．

27. 【答案】 12 cm
【解析】由折叠的性质可知，AD=BD，
∴ △ACD的周长=AC+CD+AD=AC+CD+DB=AC+BC=12cm.

28. 【答案】 150 ； 135
【解析】如图，延长 AE 到 H，
由于纸条是长方形，
∴EH∥GF，
∴∠1=∠EFG，
根据翻折不变性得 ∠1=∠2=15∘，
∴∠2=∠EFG，∠AEG=180∘−2×15∘=150∘，
又 ∵∠DEF=15∘，
∴∠2=∠EFG=15∘，∠FGD=15∘+15∘=30∘．
在梯形 FCDG 中，∠GFC=180∘−30∘=150∘，
根据翻折不变性，∠CFE=∠GFC−∠GFE=150∘−15∘=135∘．


29. 【答案】A

30. 【答案】 34
【解析】 ∵ 等腰三角形、线段、圆是轴对称图形，三角形不是轴对称图形，
∴ 从盒子中任意抽取一张，卡片上的图形是轴对称图形的概率是 34．

31. 【答案】
(1) 如图：
(2) 6；
(3) 172．
【解析】
(3) S=4×5−12×4×1−12×4×1−12×5×3=172．

32. 【答案】C
【解析】A，不是轴对称图形，故本选项不符合题意；
B，不是轴对称图形，故本选项不符合题意；
C，是轴对称图形，故本选项符合题意；
D，不是轴对称图形，故本选项不符合题意．

33. 【答案】
(1) 如图，△AʹBʹCʹ 即为所求．
(2) S△ABC=4×3−12×3×2−12×1×4−12×1×3=5.5．
(3) 如图，点 D1，D2 即为所求．

34. 【答案】C

35. 【答案】B
【解析】 ∵AB=AC，
∴∠ABC=∠C=70∘，
∴∠BAC=180∘−70∘−70∘=40∘，
∵△ABʹCʹ 与 △ABC 关于直线 AD 对称，
∴∠BAC=∠BʹACʹ=40∘，∠CAD=∠CʹAD=10∘，
∴∠BABʹ=40∘+10∘+10∘+40∘=100∘，
∵AB=ABʹ，
∴∠ABBʹ=12180∘−100∘=40∘．

36. 【答案】 513
【解析】如图，
∵ 根据轴对称图形的概念，轴对称图形两部分沿对称轴折叠后可重合，白色的小正方形有 13 个，而能构成一个轴对称图形的有 5 个情况．
∴ 使图中黑色部分的图形仍然构成一个轴对称图形的概率是：513


37. 【答案】D
【解析】A、不是轴对称图形，故此选项错误；
B、不是轴对称图形，故此选项错误；
C、不是轴对称图形，故此选项错误；
D、是轴对称图形，故此选项正确．

38. 【答案】B
【解析】如图所示：
在空白的三角形中只涂黑一个小三角形，使整个图案成轴对称图形的情况有 2 个，则概率是 29．


39. 【答案】
(1) DF+BE=EF
(2) 如图 2，延长 AP 至 T，使得 PT = AP，连接 AEʹ，AFʹ，ET，
由题可得，点 E 关于直线 AB 的对称点为 Eʹ，点 F 关于直线 AD 的对称点为 Fʹ，
∴B 为 EEʹ 的中点，D 为 FFʹ 的中点，
又 ∵ 四边形 ABCD 为正方形，
∴∠ABE=∠ADF=90∘，
∴AB 为 EEʹ 的中垂线，AD 为 FFʹ 的中垂线，
∴AE=AEʹ，AF=AFʹ，
∵ 点 P 是 EF 的中点，
∴PE=PF，
又 ∵∠EPT=∠FPA，AP=TP，
∴△PET≌△PFASAS，
∴ET=AF，∠PET=∠PFA，
∴ET=AFʹ，且 ∠AET=∠AEP+∠PET=∠AEP+∠AFP=180∘−∠EAF，
∵AEʹ=AE，AB=AB，∠ABEʹ=∠ABE=90∘，
∴Rt△ABE≌Rt△ABEʹHL，
∴∠BAEʹ=∠BAE，
同理可得 ∠FAD=∠FʹAD，
∴∠EʹAFʹ=∠BAEʹ+∠DAFʹ+∠BAD=∠BAE+∠DAF+∠BAD=∠BAD−∠EAF+∠BAD=180∘−∠EAF.
∴∠AET=∠EʹAFʹ，
又 ∵AEʹ=AE，AFʹ=ET，
∴△EʹAFʹ≌△AETSAS，
∴EʹFʹ=AT=2AP．
(3) 四边形 MEFN 的周长存在最小值 2m+n．
如图 3，作点 E 关于 AB 的对称点 Eʹ，作点 F 关于 AD 的对称点 Fʹ，连接 EʹFʹ，交 AB 于 M，交 AD 于 N，连接 ME，NF，
∵ 点 E 关于直线 AB 的对称点为 Eʹ，点 F 关于直线 AD 的对称点为 Fʹ，
∴B 为 EEʹ 的中点，D 为 FFʹ 的中点，
又 ∵ 四边形 ABCD 为正方形，
∴∠ABE=∠ADF=90∘，
∴AB 为 EEʹ 的中垂线，AD 为 FFʹ 的中垂线，
∴ME=MEʹ，NF=NFʹ，
∴四边形MEFN的周长=EM+MN+FN+EF=MEʹ+MN+NFʹ+EF=EʹFʹ+EF.
由（2）可得 EʹFʹ=2AP，由（1）可得 EF=BE+DF，
且 AP=m，BE+DF=n，
∴EʹFʹ+EF=2m+n，
∴ 当 Eʹ，M，N，Fʹ 在同一直线上时，四边形 MEFN 的周长有最小值，最小值为 2m+n．
【解析】
(1) 线段 BE，EF，DF 的数量关系是 DF+BE=EF．
理由：如图 1 所示，延长 CB 至 K，使得 BK=DF，连接 AK，则 △ABK≌△ADF，
∴AK=AF，∠BAK=∠DAF，
∴∠EAK=∠EAB+∠BAK=∠EAB+∠DAF=90∘−∠EAF=45∘，
∴∠EAK=∠EAF，
∴△EAK≌△EAFSAS，
∴EF=EK=BK+BE=DF+BE．


40. 【答案】D

41. 【答案】D

42. 【答案】D
【解析】作点 A 关于直线 l 的对称点 Aʹ，连接 BAʹ 交直线 l 于 M．
根据两点之间，线段最短，可知选项D铺设的管道，则所需管道最短．

43. 【答案】 9
【解析】由折叠可得，BE=AB=6，AD=ED，
∵AC=8，
∴AD+CD=8，
∴DE+CD=8，
又 ∵△CDE 的周长为 11，
∴CE=11−8=3，
∴BC=BE+CE=6+3=9．

44. 【答案】
(1) 如图，△AʹBʹCʹ 为所作；
(2) △ABC 的面积 =3×3−12×1×3−12×2×1−12×2×3=3.5．

45. 【答案】C

46. 【答案】
(1) △AʹBʹCʹ 即为所求．
(2) 5
(3) 如图点 P 即为所求．
【解析】
(2) S△ABC=3×4−12×2×3−12×2×2−12×1×4=5．

47. 【答案】A
【解析】A、是轴对称图形，故本选项正确；
B、不是轴对称图形，故本选项错误；
C、不是轴对称图形，故本选项错误；
D、不是轴对称图形，故本选项错误．

48. 【答案】
(1) △ABC 关于直线 MN 的对称图形如图所示；
(2) △ABC的面积=4×5−12×1×4−12×1×4−12×5×3=20−2−2−7.5=8.5.

49. 【答案】C

50. 【答案】 24°
【解析】图①中，
∵AD∥BC，
∴ 设 ∠DEF=∠EFB=α，
图②中，∠GFC=∠BGD=∠AEG=180∘−2∠EFG=180∘−2α，
图③中，∠CFE=∠GFC−∠EFG=180∘−2α−α=108．
解得 α=24∘．即 ∠DEF=24∘．

51. 【答案】D
【解析】A、不是轴对称图形，故此选项错误；
B、不是轴对称图形，故此选项错误；
C、不是轴对称图形，故此选项错误；
D、是轴对称图形，故此选项正确．

52. 【答案】B
【解析】 ∵△ADE 沿 DE 翻折，点 A 的对应点为 M，
∴DA=DM，
∵D 是边 AB 的中点，
∴DA=DB，
∴DB=DM，
∴∠DMB=∠B=70∘，
∴∠BDM=180∘−70∘−70∘=40∘．

53. 【答案】A
【解析】拿一张纸具体剪一剪，结果为 A．

54. 【答案】B
【解析】A、不是轴对称图形，故此选项错误；
B、是轴对称图形，故此选项正确；
C、不是轴对称图形，故此选项错误；
D、不是轴对称图形，故此选项错误．

55. 【答案】
(1) 如图，点 D 及四边形的另两条边 AD，DC 为所作．
(2) S四边形ABCD=2×12×4×3=12．

56. 【答案】C

57. 【答案】C
【解析】A、不是轴对称图形，故本选项不符合题意；
B、不是轴对称图形，故本选项不符合题意；
C、是轴对称图形，故本选项符合题意；
D、不是轴对称图形，故本选项不符合题意．

58. 【答案】D

59. 【答案】 4
【解析】作 A 关于 CD 的对称点 Aʹ，连接 AʹB 交 CD 于 P，则点 P 就是使 ∣PA−PB∣ 的值最大的点，
∣PA−PB∣=AʹB，
连接 AʹC，
∵△ABC 为等腰直角三角形，AC=BC=4，
∴∠CAB=∠ABC=45∘，∠ACB=90∘，
∵∠BCD=15∘，
∴∠ACD=75∘，
∴∠CAAʹ=15∘，
∵AC=AʹC，
∴AʹC=BC，∠CAʹA=∠CAAʹ=15∘，
∴∠ACAʹ=150∘，
∵∠ACB=90∘，
∴∠ACB=60∘，
∴△AʹBC 是等边三角形，
∴AʹB=BC=4．


60. 【答案】A

61. 【答案】在图中选取 3 个空白小正方形涂上阴影，使 7 个小正方形组成一个轴对称图形，如下图．

62. 【答案】 3
【解析】分别作点 P 关于 OA，OB 的对称点 C，D，
连接 CD，分别交 OA，OB 于点 M，N，
连接 OP，OC，OD，PM，PN．
∵ 点 P 关于 OA 的对称点为 C，关于 OB 的对称点为 D，
∴PM=CM，OP=OC，∠COA=∠POA；
∵ 点 P 关于 OB 的对称点为 D，
∴PN=DN，OP=3，∠DOB=∠POB，
∴OC=OD=OP=3∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60∘,
∴△COD 是等边三角形，
∴CD=OC=OD=3，
∴△PMN 的周长的最小值 =PM+MN+PN=CM+MN+DN≥CD=3．


63. 【答案】A

64. 【答案】
(1) 如图所示，△A1B1C1 即为所求．
(2) ∵C 和 C1 关于直线 l 对称，
∴PC1=PC，
∴PA+PC1=PA+PC，
当且仅当 A，P，C 三点共线时，PA+PC 取得最小值为 AC，
∴PA+PC1 的值最小为 AC．
即如图所示，直线 AC 与直线 l 的交点 P 即为所求．
(3) 4
【解析】
(3) 如图，
在正方形网格中存在 4 个格点，使得该格点与 B，C 两点构成以 BC 为底边的等腰三角形．


65. 【答案】 γ=2α+β
【解析】由折叠得：∠A=∠Aʹ，
∵∠BDAʹ=∠A+∠AFD，∠AFD=∠Aʹ+∠CEAʹ，
∵∠A=α，∠CEAʹ=β，∠BDAʹ=γ，
∴∠BDAʹ=γ=α+α+β=2α+β．


66. 【答案】 70°
【解析】延长 AB 到 Aʹ 使得 BAʹ=AB，延长 AD 到 Aʺ 使得 DAʺ=AD，
连接 AʹAʺ 与 BC，CD 分别交于点 M，N，
∵∠ABC=∠ADC=90∘，
∴A，Aʹ 关于 BC 对称，A，Aʺ 关于 CD 对称，
此时，△AMN 的周长最小，
∵BA=BAʹ，MB⊥AB，
∴MA=MAʹ，同理：NA=NAʺ，
∴∠Aʹ=∠MAB，∠Aʺ=∠NAD，
∵∠AMN=∠Aʹ+∠MAB=2∠Aʹ，
∴∠ANM=∠Aʺ+∠NAD=2∠Aʺ，∠AMN+∠ANM=2∠Aʹ+Aʺ，
∵∠BAD=125∘，
∴∠Aʹ+∠Aʺ=180∘−∠BAD=55∘，
∴∠AMN+∠ANM=2×55∘=110∘，
∴∠MAN=180∘−110∘=70∘．


67. 【答案】A

68. 【答案】
(1) 如图为所求作的四边形 ABʹCDʹ．
(2) S四边形ABCD=S△ABD+S△BCD=12×6×2+12×6×1=9.
(3) 5

【解析】
(3) 如图，作点 E 关于直线 AC 的对称点 Eʹ，连接 DEʹ 交直线 AC 于 P，点 P 即为所求，此时 PC=5．


69. 【答案】 117°

70. 【答案】C

71. 【答案】D

72. 【答案】A

73. 【答案】55

74. 【答案】
(1) 如图所示：
(2) 如图所示，AC 和 AʹCʹ 相交于点 O，
S△ABO=12×3×4=6，S△CBO=12×3×2=3．
S△ABC=S△CBO+S△ABO=6+3=9．