

2018-2019学年上海市嘉定区七上期末数学试卷
展开一、选择题(共6小题;共30分)
1. 如果 a≠0,那么下列四个选项中,正确的选项是
A. a2+a3=a5B. a2⋅a3=a6C. a23=a8D. a2÷a3=1a
2. 下列各选项中的两个单项式,属于同类项的是
A. −2x,2yB. 2xy,xyzC. −xy2,13y2xD. xy2,x2y
3. 下列四个选项中,正确的选项是
A. a−b=b−aB. a−b=−b−a
C. −−a−b=a−bD. −a+b=−a+b
4. 下列四个选项中,可以表示 x2x+1−1x+1 的计算结果的选项是
A. x2−1B. x−1C. x−12D. x−12x+1
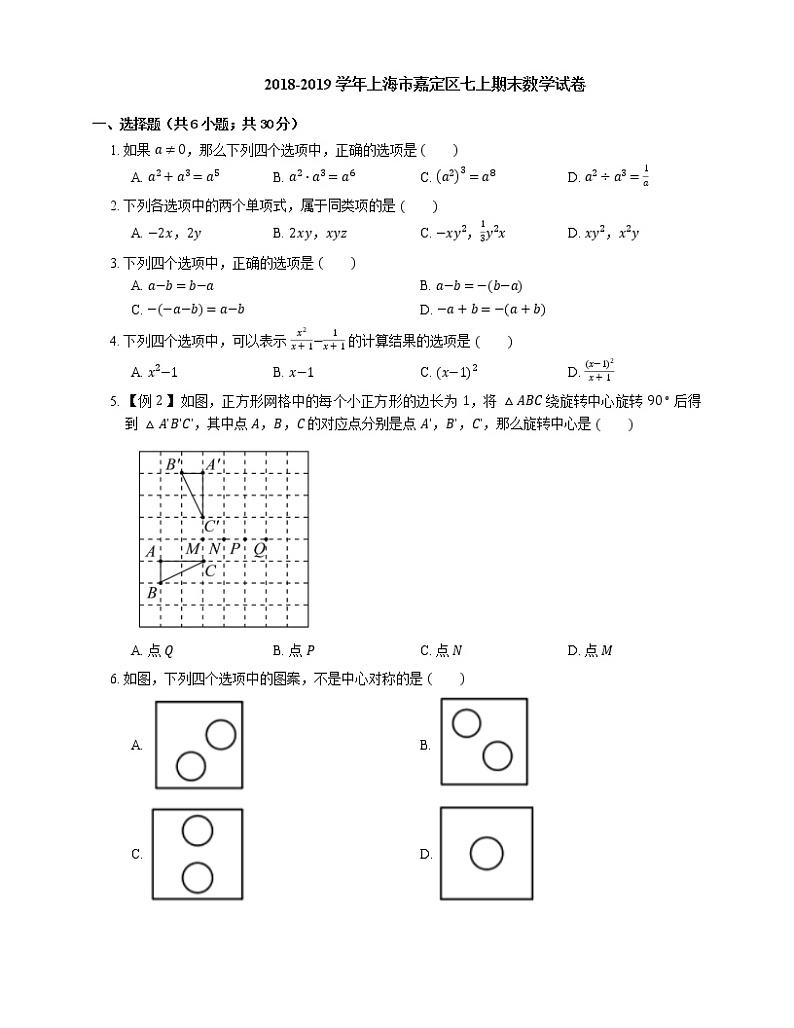
5. 【例 2 】如图,正方形网格中的每个小正方形的边长为 1,将 △ABC 绕旋转中心旋转 90∘ 后得到 △AʹBʹCʹ,其中点 A,B,C 的对应点分别是点 Aʹ,Bʹ,Cʹ,那么旋转中心是
A. 点 QB. 点 PC. 点 ND. 点 M
6. 如图,下列四个选项中的图案,不是中心对称的是
A. B.
C. D.
二、填空题(共12小题;共60分)
7. 计算:3x2−4x2= .
8. 地球与太阳的距离是 1.5×108 千米,光的速度约是每秒 3×105 千米,那么太阳光射到地球需要的时间为 秒.
9. 计算:−2x0= (备注:x≠0).
10. 因式分解:ax+ay+bx+by= .
11. 要使代数式 42x+3 有意义,那么字母 x 所表示的数的取值范围是 .
12. 写出多项式 x2−y2 与多项式 x2+xy 的一个公因式 .
13. 分式 1x2−y2 与分式 1x2−xy 的最简公分母是 .
14. 计算:−2x3÷12x2= .
15. 将代数式 3x−2y3 表示为只含有正整数指数幂的形式:3x−2y3= .
16. 如果代数式 x2+2mx+16 是只关于 x 的完全平方式,那么字母 m 所表示的数是 .
17. 如图,将三角形 ABC 沿直线 BC 平移得到三角形 DEF,其中点 A 与点 D 是对应点,点 B 与点 E 是对应点,点 C 与点 F 是对应点,如果 BC=5,EC=2,那么线段 AD 的长是 .
18. 已知线段 AB=2,以点 A 为旋转中心,如果将 AB 顺时针旋转 120∘,那么线段 AB 所扫过的图形的面积为 .(答案保留 π)
三、解答题(共7小题;共91分)
19. 计算:x+y−2x−y.
20. 计算:
(1)x2−5x+6x2+3x+2÷x−2x+1.
(2)xx2−y2−1x+y.
21. 已知:三角形纸片 ABC,∠C=90∘(如图).点 E 在线段 AC 上,点 F 在线段 AB 上,且点 A 与点 B 关于直线 EF 对称.
(1)画出直线 EF,并连接 BE.
(2)如果 AC=4,BC=3,求三角形 BCE 的周长.
22. 先化简,再求值:3a+2+a−2÷a2+2a+1a+2,其中 a=3.
23. 请回答下列问题:
(1)如果关于 x 的分式方程 m−2x+1=1 无解,求字母 m 的值.
(2)如果关于 x 的分式方程里 m−2x+1=1 的解是负数,求字母 m 的取值范围.
24. 某工厂计划生产 480 个零件,当生产任务完成一半时,停止生产进行反思和改进,用时 20 分钟.恢复生产后工作效率比原来可以提高 20%,要求比原计划提前 40 分钟完成任务,那么反思改进后每小时需要生产多少个零件?
25. 如图 1,将边长为 a 的正方形的边长增加 b,得到一个边长为 a+b 的正方形.在图 1 的基础上,某同学设计了一个解释验证 a+b2=a2+2ab+b2 的方案(详见方案 1)
方案 1.如图 2,用两种不同的方式表示边长为 a+b 的正方形的面积.
方式 1:S=a+b2
方式 2:S=S1+S2+S3+S4=a2+ab+ab+b2=a+b2=a2+2ab+b2
因此,a+b2=a2+2ab+b2.
(1)请模仿方案 1,在图 1 的基础上再设计一种方案,用以解释验证 a+b2=a2+2ab+b2.
(2)如图 3,在边长为 a 的正方形纸片上剪掉边长为 b 的正方形,请在此基础上再设计一个方案用以解释验证 a2−b2=a+ba−b.
答案
第一部分
1. D【解析】A.原式=a2+a3,故A错误;
B.原式=a5,故B错误;
C.原式=a6,故C错误.
2. C
3. B
4. B【解析】x2x+1−1x+1=x2−1x+1=x+1x−1x+1=x−1.
5. C
【解析】如图,N 点为旋转中心.
故选:C.
6. A
第二部分
7. −x2
【解析】3x2−4x2=−x2.
8. 5×102
【解析】由 s=vt,
t=1.5×1083×105=0.5×103=5×102(秒).
9. −2
【解析】−2x0=−2(备注:x≠0).
10. a+bx+y
【解析】原式=ax+y+bx+y=a+bx+y.
11. x≠−32
【解析】由分式有意义的条件可知:2x+3≠0,
∴x≠−32,
故答案为:x≠−32.
12. x+y
【解析】∵x2−y2=x+yx−y,x2+xy=xx+y,
∴ 两个多项式的公因式为:x+y.
13. xx+yx−y
【解析】两个分式可化为:1x+yx−y,1xx−y,
故最简公分母:xx+yx−y.
14. −8x
【解析】−2x3÷12x2=−2x3÷14x2=−8x.
15. 3y3x2
【解析】将代数式 3x−2y3 表示为只含有正整数指数幂的形式:3x−2y3=3y3x2.
故答案为:3y3x2.
16. 4 或 −4
【解析】∵x±42=x2±8x+16,
∴±8=2m,
∴m=±4.
17. 3
【解析】根据平移的性质可得:BE=CF=BC−EC=5−2=3,
∴AD=BE=3.
18. 4π3
【解析】由题意:扇形的面积 =120⋅π⋅22360=4π3.
第三部分
19. 原式=x2−xy+xy−y2−2x+2y=x2−y2−2x+2y.
20. (1) 原式=x−2x−3x+1x+2⋅x+1x−2=x−3x+2.
(2) 原式=xx+yx−y−x−yx+yx−y=yx+yx−y=yx2−y2.
21. (1) 如图所示,直线 EF 即为所求.
(2) 由(1)知 AE=BE,
∵AC=AE+CE=4,
∴BE+CE=4,又 BC=3,
∴BE+CE+BC=7,
即三角形 BCE 的周长为 7.
22. 3a+2+a−2÷a2+2a+1a+2=3+a+2a−2a+2⋅a+2a+12=a2−1a+2⋅a+2a+12=a+1a−1a+2⋅a+2a+12=a−1a+1.
当 a=3 时,
原式=3−13+1=12.
23. (1) 两边乘以 x+1,得:m−2=x+1,
由题意知 x=−1,代入得 m−2=0,
则 m=2.
(2) 两边乘以 x+1,得:m−2=x+1,
解得 x=m−3,
由题意知 m−3<0,且 m−3≠−1,
解得:m<3 且 m≠−2.
24. 设改进后每小时需要生产 x 个零件,则原来每小时生产 x1+20%=56x 个零件,
由题意得,
1+240x=24056x,
解得,
x=48,
经检验:x=48 是原方程的根,且符合题意.
答:改进后每小时需要生产 48 个零件.
25. (1) 如图所示.
(2) 如图所示.
2018-2019学年上海市闵行区颛桥中学七上期中数学试卷: 这是一份2018-2019学年上海市闵行区颛桥中学七上期中数学试卷,共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2018-2019学年上海市杨浦区七上期中数学试卷: 这是一份2018-2019学年上海市杨浦区七上期中数学试卷,共5页。试卷主要包含了填空题,选择题,解答题等内容,欢迎下载使用。
2018-2019学年上海市宝山区七上期末数学试卷: 这是一份2018-2019学年上海市宝山区七上期末数学试卷,共9页。试卷主要包含了填空题,选择题,解答题等内容,欢迎下载使用。












