2019-2020学年山东省青岛市李沧区八上期末数学试卷

这是一份2019-2020学年山东省青岛市李沧区八上期末数学试卷，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共8小题；共40分）
1. 3 的算术平方根是
A. ±3B. 3C. −3D. 9

2. 在庆祝新中国成立 70 周年的校园歌唱比赛中，11 名参赛同学的成绩各不相同，按照成绩取前 5 名进入决赛．如果小明知道了自己的比赛成绩，要判断能否进入决赛，小明需要知道这 11 名同学成绩的
A. 平均数B. 中位数C. 众数D. 方差

3. 已知 M1,−2，N−3,−2，则直线 MN 与 x 轴，y 轴的位置关系分别为
A. 相交，相交B. 平行，平行C. 垂直，平行D. 平行，垂直

4. 通讯员要骑车到达某地．若他每小时行驶 15 千米，则提前 24 分钟到达；若他每小时行驶 12 千米，则要迟到 15 分钟．设通讯员到达某地的路程是 x 千米，原定的时间为 y 小时，则可列方程组为
A. x15−24=y,x12+15=yB. x15+24=y,x12−15=yC. x15−2460=y,x12+1560=yD. x15+2460=y,x12−1560=y

5. 下列根式中，是最简二次根式的是
A. 8B. 12C. 6D. 27

6. 下列各组数据中，方差最小的是
A. 1，2，3，4B. 3，3，3.14，10C. 2，4，6，8D. 2，3，4，5

7. 如图，小明从 A 处出发沿北偏东 40∘ 方向行走至 B 处，又从点 B 处沿东偏南 20∘ 方向行走至 C 处，则 ∠ABC 等于
A. 130∘B. 120∘C. 10∘D. 100∘

8. 在平面直角坐标系中，一个智能机器人接到如下指令：从原点 O 出发，按向右，向上，向右，向下的方向依次不断移动，每次移动 1 m．其行走路线如图所示，第 1 次移动到 A1，第 2 次移动到 A2，⋯，第 n 次移动到 An．则 △OA2A2020 的面积是
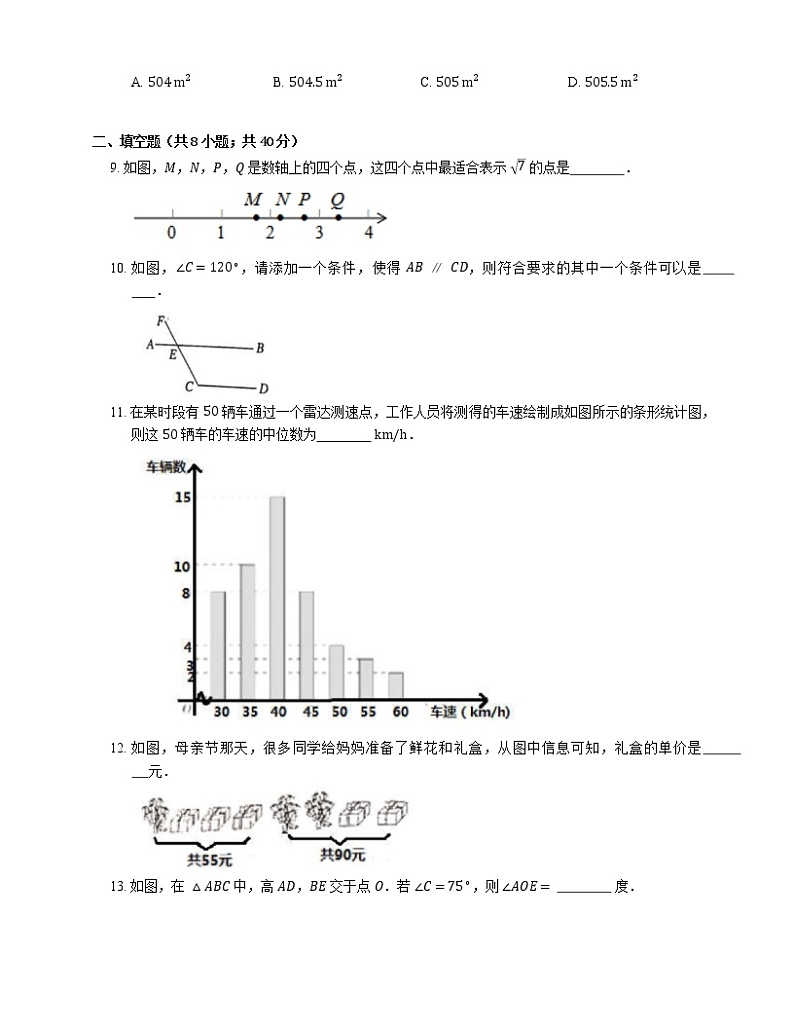
A. 504 m2B. 504.5 m2C. 505 m2D. 505.5 m2

二、填空题（共8小题；共40分）
9. 如图，M，N，P，Q 是数轴上的四个点，这四个点中最适合表示 7 的点是 ．

10. 如图，∠C=120∘，请添加一个条件，使得 AB∥CD，则符合要求的其中一个条件可以是 ．

11. 在某时段有 50 辆车通过一个雷达测速点，工作人员将测得的车速绘制成如图所示的条形统计图，则这 50 辆车的车速的中位数为 km/h．

12. 如图，母亲节那天，很多同学给妈妈准备了鲜花和礼盒，从图中信息可知，礼盒的单价是 元．

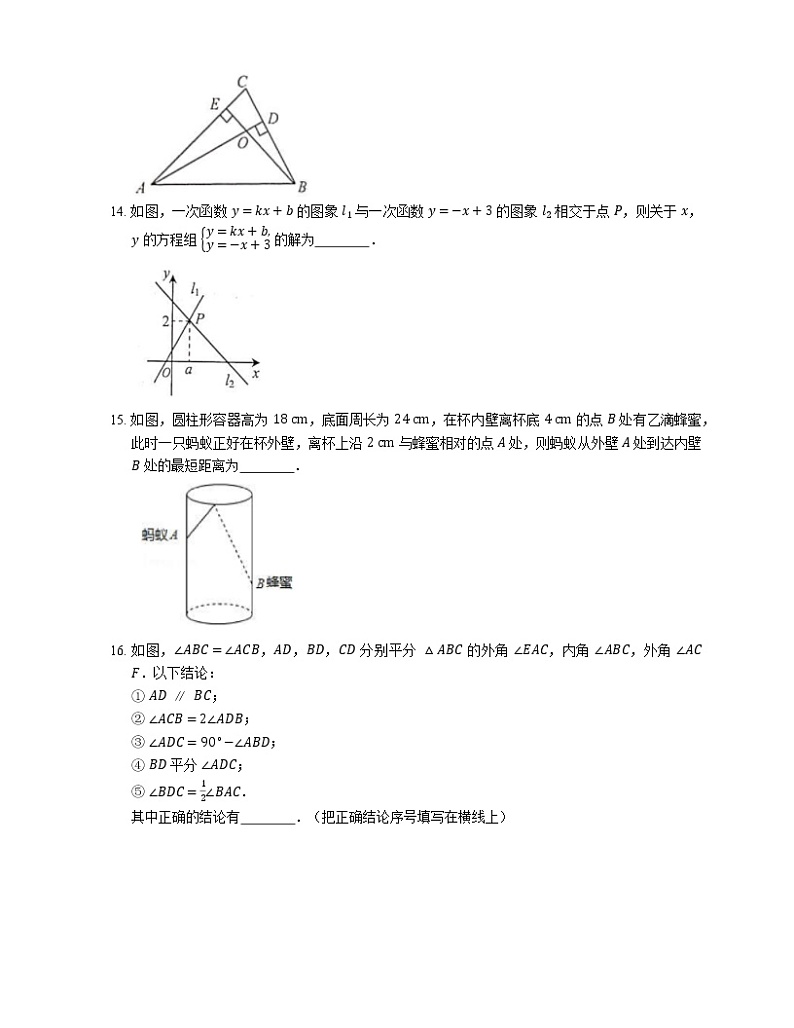
13. 如图，在 △ABC 中，高 AD，BE 交于点 O．若 ∠C=75∘，则 ∠AOE= 度．

14. 如图，一次函数 y=kx+b 的图象 l1 与一次函数 y=−x+3 的图象 l2 相交于点 P，则关于 x，y 的方程组 y=kx+b,y=−x+3 的解为 ．

15. 如图，圆柱形容器高为 18 cm，底面周长为 24 cm，在杯内壁离杯底 4 cm 的点 B 处有乙滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿 2 cm 与蜂蜜相对的点 A 处，则蚂蚁从外壁 A 处到达内壁 B 处的最短距离为 ．

16. 如图，∠ABC=∠ACB，AD，BD，CD 分别平分 △ABC 的外角 ∠EAC，内角 ∠ABC，外角 ∠ACF．以下结论：
① AD∥BC；
② ∠ACB=2∠ADB；
③ ∠ADC=90∘−∠ABD；
④ BD 平分 ∠ADC；
⑤ ∠BDC=12∠BAC．
其中正确的结论有 ．（把正确结论序号填写在横线上）

三、解答题（共8小题；共104分）
17. 请回答下列问题：
（1）求值：−10−4．
（2）计算：13+5−5+33．
（3）解方程组：4s+3t=5,2s−t=−5.
（4）解方程组：12x+710y=35,x+25y=40.

18. 如图，有三个论断：① ∠1=∠2；② ∠B=∠C；③ ∠A=∠D，请你从中任选两个作为条件，另一个作为结论构成一个命题，并证明该命题的正确性．

19. 为了提高农田利用效益，某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾 ⋅ 稻”轮作模式．某农户去年开始实施“虾 ⋅ 稻”轮作，去年出售小龙虾每千克获得的利润为 32 元．由于开发成本下降和市场供求关系变化，今每千克小龙虾的养殖成本下降 25%，售价下降 10%，出售小龙虾每千克获得利润为 30 元．求去年每千克小龙虾的养殖成本与售价．

20. 实验证明，平面镜反射光线的规律是：照射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．
（1）如图，一束光线 MA 照射到平面镜 CE 上，被 CE 反射到平面镜 CF 上，又被 CF 反射．已知被 CF 反射出的光线 BN 与光线 MA 平行．若 ∠1=35∘，则 ∠2= ，∠3= ；若 ∠1=50∘，∠3= ．
（2）由（1）猜想：当两平面镜 CE，CF 的夹角 ∠3 为多少度时，可以使任何射到平面镜 CE 上的光线 MA，经过平面镜 CE，CF 的两次反射后，入射光线 MA 与反射光线 BN 平行，请你写出推理过程．

21. 某单位欲招聘管理人员一名，对甲、乙、丙三名候选人进行了笔试和面试两项测试，三人的测试成绩如下表所示：
根据录用程序，组织 200 名职工对三人利用投票推荐的方式进行民主评议，三人得票率（没有弃权票，每位职工只能推荐 1 人）的扇形统计图如图所示，每得一票记作 1 分．
（1）请算出这三人的民主评议得分；
（2）根据实际需要，单位将笔试、面试、民主评议三项测试得分按 4:3:3 的比例确定个人成绩，那么谁将被录用?

22. 亚洲文明对话大会召开期间，大批的大学生志愿者参与服务工作．某大学计划组织本校全体志愿者统一乘车去会场，若单独调配 36 座新能源客车若干辆，则有 2 人没有座位；若只调配 22 座新能源客车，则用车数量将增加 4 辆，并空出 2 个座位．
（1）计划调配 36 座新能源客车多少辆?该大学共有多少名志愿者?
（2）若同时调配 36 座和 22 座两种车型，既保证每人有座，又保证每车不空座，则两种车型各需多少辆?

23. 我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为 1 的分数），那么无限循环小数如何表示为分数形式呢?请看以下示例：
例：将 0.1 化为分数形式，
由于 0.1=0.111⋯，
设 x=0.111, ⋯⋯①
则 10x=1.111, ⋯⋯②
② − ①得 9x=1，解得 x=19，于是得 0.1=19⋯．
同理可得 0.6=69=23，2.5=2+0.5=2+59=239．
根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）
（1）0.4= ，2.8= ；
（2）将 0.45 化为分数形式，写出推导过程；
（3）0.234= ，1.036= ；（注：0.234=0.234234⋯，1.036=1.03636⋯）
（4）①试比较 1.9 与 2 的大小：1.9 2（填“>”“