2018_2019学年天津市河东区八上期末数学试卷

这是一份2018_2019学年天津市河东区八上期末数学试卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共12小题；共60分）
1. 下列图形中，是轴对称图形的是
A. B.
C. D.

2. 分式 2x+1 有意义，则 x 的取值范围是
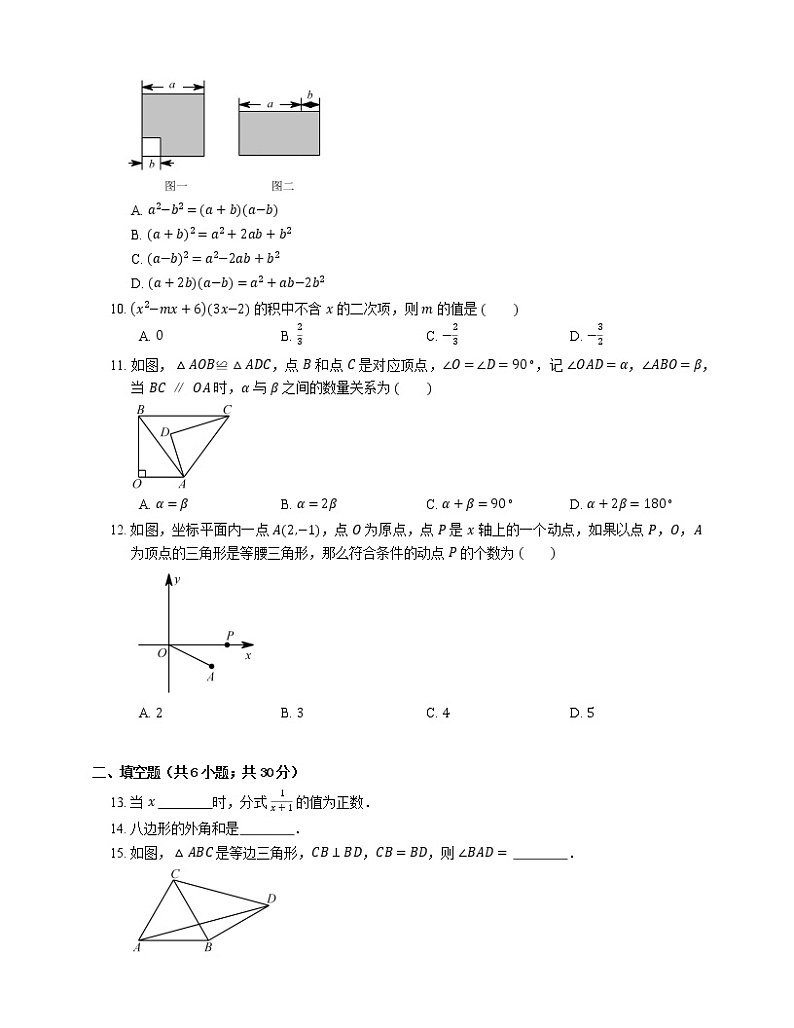
A. x>1B. x≠−1C. xb），把余下的部分剪成一个矩形（如图（二）），通过计算两个图形（阴影部分）的面积，验证了一个等式，则这个等式是
A. a2−b2=a+ba−b
B. a+b2=a2+2ab+b2
C. a−b2=a2−2ab+b2
D. a+2ba−b=a2+ab−2b2

10. x2−mx+63x−2 的积中不含 x 的二次项，则 m 的值是
A. 0B. 23C. −23D. −32

11. 如图，△AOB≌△ADC，点 B 和点 C 是对应顶点，∠O=∠D=90∘，记 ∠OAD=α，∠ABO=β，当 BC∥OA 时，α 与 β 之间的数量关系为
A. α=βB. α=2βC. α+β=90∘D. α+2β=180∘

12. 如图，坐标平面内一点 A2,−1，点 O 为原点，点 P 是 x 轴上的一个动点，如果以点 P，O，A 为顶点的三角形是等腰三角形，那么符合条件的动点 P 的个数为
A. 2B. 3C. 4D. 5

二、填空题（共6小题；共30分）
13. 当 x 时，分式 1x+1 的值为正数．

14. 八边形的外角和是 ．

15. 如图，△ABC 是等边三角形，CB⊥BD，CB=BD，则 ∠BAD= ．

16. 如图，点 C 是 AB 的中点，AD=CE，若添加一个条件使 △ACD≌△CBE，你添加的条件是 ．

17. 若 ∣m−1∣+n2−18n+81=0，将 mx2−ny2 因式分解得 ．

18. 如图，点 C 为线段 AE 上一动点（不与点 A，E 重合），在 AE 同侧分别作正 △ABC 和正 △CDE，AD 与 BE 交于点 O，AD 与 BC 交于点 P，BE 与 CD 交于点 Q，连接 PQ．以下五个结论：① AD=BE；② PQ∥AE；③ AP=BQ；④ DE=DP；⑤ ∠AOB=60∘．恒成立的结论有 （把你认为正确的序号都填上）．

三、解答题（共7小题；共91分）
19. 计算题：
（1）m+2n3n−m；
（2）2xx2−64y2−1x−8y．

20. 如图所示的坐标系中，△ABC 的三个顶点的坐标依次为 A2,4，B−3,−2，C3,1．
（1）请在这个坐标系中作出 △ABC 和关于 y 轴对称的 △A1B1C1．
（2）分别写出点 A1，B1，C1 的坐标．

21. 分解因式：
（1）8a3b2+12ab3c；
（2）2x+y2−x+2y2．

22. 解方程：
（1）2x−1=4x2−1．
（2）x−3x−2+1=32−x．

23. 如图：点 B，E，C，F 在一条直线上，FB=CE，AB∥ED，AC∥DF．求证：AB=DE，AC=DF．

24. 某超市用 4000 元购进某种服装销售，由于销售状况良好，超市又调拨 9000 元资金购进该种服装，但这次的进价比第一次的进价降低了 10%，购进的数量是第一次的 2 倍还多 25 件，问这种服装的第一次进价是每件多少元?

25. 如图 1，在 △ABC 中，∠B=60∘，点 M 从点 B 出发沿射线 BC 方向，在射线 BC 上运动．在点 M 运动的过程中，连接 AM，并以 AM 为边在射线 BC 上方，作等边 △AMN，连接 CN．
（1）当 ∠BAM= ∘ 时，AB=2BM；
（2）请添加一个条件： ，使得 △ABC 为等边三角形；
①如图 1，当 △ABC 为等边三角形时，求证：BM=CN；
②如图 2，当点 M 运动到线段 BC 之外时，其它条件不变，①中结论 BM=CN 还成立吗?请说明理由．
答案
第一部分
1. B
2. B【解析】由题意，得 x+1≠0，解得 x≠−1．
3. B【解析】因为 x3⋅x=x3+1=x4≠x3，故选项A错误；
x+y2=x2+2xy+y2=x2+y2+2xy，故选项B正确；
xx−2=x2−2x≠−2x−x2，故选项C错误；
3x3y2÷xy2=3x3−1y2−2=3x2≠3x4，故选项D错误．
4. C【解析】A．x2+xy5x+xy=x+y5+y；
B．x2−4x+2=x−2；
C．5x2−1 的分子、分母都不能再分解，且不能约分，是最简分式；
D．x2+6x+9x2−9=x+3x−3．
5. A
6. C
7. D【解析】∵a−22+∣b−3∣=0，
∴a−2=0，b−3=0，
解得 a=2，b=3，
①当腰是 2，底边是 3 时，三边长是 2，2，3，此时符合三角形的三边关系定理，即等腰三角形的周长是 2+2+3=7；
②当腰是 3，底边是 2 时，三边长是 3，3，2，此时符合三角形的三边关系定理，即等腰三角形的周长是 3+3+2=8．
8. C【解析】∵x2−mx+14 是完全平方式，
∴x2−mx+14=x±122，
∴m=±1．
9. A【解析】由题可得：a2−b2=a−ba+b．
10. C
【解析】x2−mx+63x−2=3x3−2+3mx2+2m+18x−12，
因为 x2−mx+63x−2 的积中不含 x 的二次项，
所以 2+3m=0，解得，m=−23．
11. B【解析】∵△AOB≌△ADC，
∴AB=AC，∠BAO=∠CAD，
∴∠BAC=∠OAD=α，
在 △ABC 中，∠ABC=12180∘−α，
∵BC∥OA，
∴∠OBC=180∘−∠O=180∘−90∘=90∘，
∴β+12180∘−α=90∘，
整理得，α=2β．
12. C【解析】如图：
① OA 为等腰三角形底边，符合符合条件的动点 P 有一个；
② OA 为等腰三角形一条腰，符合符合条件的动点 P 有三个．
综上所述，符合条件的点 P 的个数共 4 个．
第二部分
13. >−1
【解析】由题意可知：x+1>0，
∴x>−1．
14. 360∘
15. 15∘
【解析】∵△ABC 是等边三角形，CB⊥BD，
∴∠ABD=150∘，
∵CB=BD，AB=BC，
∴AB=BD，
∴∠BAD=∠BDA=12180∘−150∘=15∘．
16. CD=BE 或 ∠A=∠BCE
【解析】添加 CD=BE 或 ∠A=∠BCE 后可分别根据 SSS，SAS 判定 △ACD≌△CBE．
17. x+3yx−3y
【解析】因为 ∣m−1∣+n2−18n+81=0，
所以 m=1，n=9，
则 mx2−ny2=x2−9y2=x+3yx−3y．
18. ①②③⑤
【解析】① ∵ 正 △ABC 和正 △CDE，
∴AC=BC，CD=CE，∠ACB=∠DCE=60∘，
∵∠ACD=∠ACB+∠BCD，∠BCE=∠DCE+∠BCD，
∴∠ACD=∠BCE，
∴△ADC≌△BECSAS，
∴AD=BE，∠ADC=∠BEC（故①正确）；
②又 ∵CD=CE，∠DCP=∠ECQ=60∘，∠ADC=∠BEC，
∴△CDP≌△CEQASA．
∴CP=CQ，
∴∠CPQ=∠CQP=60∘，
∴∠QPC=∠BCA，
∴PQ∥AE（故②正确）；
③ ∵△CDP≌△CEQ，
∴DP=QE，
∵△ADC≌△BEC，
∴AD=BE，
∴AD−DP=BE−QE，
∴AP=BQ（故③正确）；
④ ∵DE>QE，且 DP=QE，
∴DE>DP（故④错误）；
⑤ ∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60∘（故⑤正确）．
∴ 正确的有：①②③⑤．
第三部分
19. （1） m+2n3n−m=3mn−m2+6n2−2mn=mn−m2+6n2.
（2） 2xx2−64y2−1x−8y=2xx+8yx−8y−x+8yx−8yx+8y=x−8yx+8yx−8y=1x+8y.
20. （1） 如图所示，
△ABC 和 △A1B1C1 即为所求．
（2） 点 A1 的坐标为 −2,4，B1 的坐标为 3,−2，C1 的坐标为 −3,1．
21. （1） 8a3b2+12ab3c=4ab22a2+3bc．
（2） 2x+y2−x+2y2=2x+y+x+2y2x+y−x−2y=3x+yx−y.
22. （1） 由原方程，得
2x+1=4.2x=4−2.x=1.
检验：当 x=1 时，x+1x−1=0．
所以原方程无解．
（2） 由原方程，得
x−3+x−2=−3.2x=−3+5.x=1.
检验：当 x=1 时，x−2≠0，
所以 x=1 是原方程的根．
23. ∵FB=EC，
∴BC=EF，
∵AB∥ED，AC∥DF，
∴∠B=∠E，∠ACB=∠DFE，
在 △ABC 与 △DEF 中，
∵∠B=∠E,BC=EF,∠ACB=∠DFE,
∴△ABC≌△DEFASA，
∴AB=DE，AC=DF．
24. 设这种服装第一次进价是每件 x 元，根据题意，得：
90001−10%x=2×4000x+25.
解得：
x=80.
经检验 x=80 是原分式方程的解，
答：这种服装第一次进价是每件 80 元．
25. （1） 30
【解析】当 ∠BAM=30∘ 时，
∴∠AMB=180∘−60∘−30∘=90∘，
∴AB=2BM．
（2） AB=AC
① ∵△ABC 与 △AMN 是等边三角形，
∴AB=AC，AM=AN，∠BAC=∠MAN=60∘，
∴∠BAC−∠MAC=∠MAN−∠MAC，即 ∠BAM=∠CAN，
在 △BAM 与 △CAN 中，
AB=AC,∠BAM=∠CAN,AM=AN,
∴△BAM≌△CANSAS，
∴BM=CN；
②成立，理由如下；
∵△ABC 与 △AMN 是等边三角形，
∴AB=AC，AM=AN，∠BAC=∠MAN=60∘，
∴∠BAC+∠MAC=∠MAN+∠MAC，即 ∠BAM=∠CAN，
在 △BAM 与 △CAN 中，
AB=AC,∠BAM=∠CAN,AM=AN,
∴△BAM≌△CANSAS，
∴BM=CN．